УРОК №1

Тема. Пряма і обернена пропорційні залежності.

Мета: ознайомити учнів з прямою і оберненою пропорційними залежностями, формувати в учнів уміння й навички застосування й навички застосування їх до розв’язування задач, розвивати пізнавальний інтерес, прищеплювати любов до математики.

ХІД УРОКУ

I.Організаційний момент.

II.Мотивація навчання.

Вступне слово вчителя.

Ви вже знайомі з основними поняттями теми “ Відношення і пропорції”, але систематизованих знань іще не маєте. Поняття пропорційної залежності відіграє велику роль не тільки в математиці, а й у фізиці, біології, хімії, у сільському господарстві, а також у будівництві, мистецтві. Усі знають, що найкращий спосіб вивчити і запам’ятати – це зробити відкриття самому. Будемо робити відкриття.

III. Вивчення нового матеріалу.

Задача 1 Швидкість автобуса 50 км/год. Який шлях він проїде за 1 год.? 2год? 3,5 год ?  6 год? Результати записати у таблицю

 

Таблиця1

Швидкість, км /год	50	50	50	50	50
Час, год	1	2	3	3,5	6
Шлях, км	50	100	150	175	300

 

Бачимо що шлях дорівнює добутку швидкості і часу руху: s=vt.

Запитання

1.        Скільки величин розглядається у задачі?
2.        Які величини змінюються, а які залишаються сталими?
3.        Скласти кілька відношень шляху до часу.
4.        Який висновок можна зробити?

(Усі відношення рівні між собою дорівнюють швидкості автобуса.)

 Якщо дві величини змінюються так, що відношення відповідних значень цих величин є сталим числом, то такі величини називаються прямо пропорційними.

Прямо пропорційні: s=vt.

Наведіть приклад.

Учень: 1 хлібина коштує 1 грн.,

  2 хлібини – 2 грн.,

  7 хлібин – 7 грн.

Прочитайте інше означення прямої пропорційності в підручнику.

Приклад: .

Задача 2. Відстань між селами 16 км. З якою швидкістю слід рухатися, щоб подолати цю відстань за 1 год? 2 год? 4 год? 8 год? 16 год? Результати записати у таблицю.

Таблиця1

Шлях, км	16	16	16	16	16
Час, год	1	2	4	8	16
Швидкість, км /год	16	8	4	2	1

 

Запитання

1.   Скільки величин розглядається у задачі?
2.   Які величини змінюються, а які залишаються сталими?
3.   Скласти кілька рівностей.
4.   Який висновок можна зробити?

(Час і швидкість – змінні величини, але їх добуток сталий.)

vt = 116 = 28 = 44 = 82 = 161.

Якщо дві величини змінюються так, що добуток відповідних значень цих величин є сталим числом, то такі величини називаються обернено пропорційними.

Обернено пропорційні:

.

Наведіть приклад.

Учень: 1 робітник виконає певну роботу за 8 год.,

  2 робітника - за 4 год.,

  4 робітник - за 1 год.

Інше означення оберненої пропорційності прочитайте в підручнику.

Можна дати інше означення прямої і оберненої пропорційності.

Якщо дві змінні величини зв’язані між собою так, що із збільшенням (зменшенням) однієї з них у кілька разів значення другої збільшується (зменшується) у стільки ж разів, то такі величини називаються прямо пропорційними.

Якщо дві змінні величини зв’язані між собою так, що із збільшенням (зменшенням) однієї з них у кілька разів значення другої зменшується (збільшується) у стільки ж разів, то такі величини обернено пропорційними.

 

IV. Закріплення вивченого матеріалу.

1. № 549 (усно). Прямо чи обернено пропорційні величини:

а) маса товару та його вартість (прямо пропорційні);

б) швидкість і час при сталій відстані (обернено пропорційні);

в) кількість робітників і час виконання певної роботи (обернено пропорційні);

г) маса тіла і його об’єм (обернено пропорційні);

д) довжина і ширина прямокутника при сталій площі (обернено пропорційні).

V. Домашнє завдання. Вивчити правила. Прочитати за підручником п.6.3.,розв”язати  № 528,529.

УРОК №2

Тема.  Задачі на пропорційний поділ.

Мета: формувати вміння знаходити невідомий член пропорції, розв’язувати задачі на пропорційний поділ і логічного характеру, виховувати інтерес до предмета.

ХІД УРОКУ

1. Організаційний момент.

II.Актуалізація опорних знань.

1. Оцінити кросворди, кращі використати під час проведення математичного тижня.

2.Колективне розв’язування задачі.

Знайти периметр квадрата зі стороною 4м. Чи є периметр і сторона квадрата прямо пропорційними величинами? Чому?

Розв’язання

1) Знайдемо периметр квадрата:

Р= 4а, Р = , Р = 16 м.

2) Знайдемо відношення периметра до сторони

P : a = 16 : 4, = 4

Відповідь. Периметр квадрата і його сторона є прямо пропорційними

величинами, оскільки

III Мотивація навчальної діяльності

Задача.Оля купила 24 яблука, які розділила між татом, мамою і собою у відношенні  3 : 2 : 1 . Скільки яблук отримав кожний?

Колективно розв’язуємо  задачу.

 1 –й спосіб ( з використанням властивості пропорції)

1) 3 + 2 + 1 = : ( частин ) становлять яблука.

2) Тато отримав 3 частини. Запишемо схему:

24 яблука – 6 частин

х яблук – 3 частини.

Складемо пропорцію:

24 х = 6 3,

х = = 12

12 яблук отримав тато.

3) Мама отримала 2 частини. Запишемо схему і складемо пропорцію.

24 яблука – 6 частин,

х яблук – 2 частина.

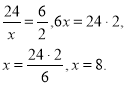
8 яблук отримала мама.

4) Одну частину отримала Оля.

24 яблука – 6 частин,

х яблук – 1 частина.

4 яблука отримала Оля.

2-й спосіб

1) 3+2+1=3 (частин) становлять яблука.

2) 24:6=4 (яблука) припадає на одну частину.

3) 43= 12 (яблук отримав тато).

4) 42= 8 (яблук отримала мама).

5) 41= 4 (яблук отримала Оля).

IV. Самостійна робота.

1-й варіант

Задача №1

Сплав складається з міді, олова і сурми, які взято у відношенні 1:2:2. Скільки треба взяти кожної з цих речовин, щоб дістати 0,792 т сплаву.

Розв’язок

1.               1+2+2=5 (частин) становить сплав.
2.               Мідь становить 1 частину. Запишемо схему.

0,792 т – 5 част.

х т - 1 част.

Складемо пропорцію.

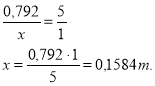
0,158 т становить мідь.

3.               Олово становить 2 частини. Запишемо схему.

0,792 т – 5 част.

х т - 2 част.

Складемо пропорцію.

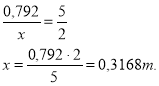
0,3168 т становить олово і 0,3168 т становить сурма.

Відповідь

а) 0,3168 т становить олово,

б) 0,3168 т становить сурма,

в) 0,158 т становить мідь.

Задача №2

Поділити число 60 на частини у відношенні 235.

Розв’язок

1) 2+3+5=10 частин

60 – 10 частин                          60 – 10 частин         60 – 10 частин

х – 2 частини                           х – 3 частини          х – 5 частини

    

 

 

 

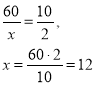
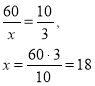
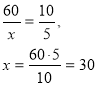
Відповідь

а) перше число 12,

б) друге число 18,

в) трете число 30.

 

2-й варіант

Задача №1

Вода складається з 2 частин водню і 16 частин кисню (за масою). Скільки кисню (за масою) міститься в 5,4 л води?

Задача №2

Сума кутів трикутника дорівнює 180⁰. Знайти ці кути, якщо вони пропорційні до чисел 5, 6, 7.

 

УРОК №3

Тема.  Розв’язування задач.

Мета: продовжити формування навичок розв’язування задач, що містять відсотки, показати їх застосування в практичній діяльності, сприяти активізації розумової діяльності, розвивати бажання застосовувати набуті знання.

ХІД УРОКУ

1. Організаційний момент.

II.Актуалізація опорних знань.

 

1. Два учні виконують завдання біля дошки, а два за партою.

1. Периметр трикутника 130.  см., сторони відносяться як 7 : 9 : 10. Знайти довжини сторін.

2. Латунь – це сплав міді та цинку, маси яких відносяться як 3 : 2. Скільки треба цинку, щоб виплавити 120 кг. Латуні?

3. 280 підручників розподілили між трьома школами у відношенні 4 : 3 : 5. Скільки підручників отримала кожна школа?

4. Поділити число 480 на частини у відношенні 3 : 5 : 4.

2. Колективне розв’язування задачі.

Довжина парку прямокутної форми на 400 м. Більша від ширини, відношення довжини до ширини 5 : 3. Скільки часу потрібно пішоходу, щоб обійти парк, якщо його швидкість 3 км/год.?

Розв’язання

Позначимо ширину парку через х тоді його довжина ( х + 400) м., а їх відношення запишемо пропорцією:

( х + 400) : х = 5 : 3.

Знайдемо х.

5х = 3 ( х + 400 )

5х = 3х + 1200

5х – 3х = 1200

2х = 1200

х = 600

Ширина парку 600м., а довжина парку 600 + 400 = 1000 (м.).

Знайдемо периметр парку:

Р = 2(а = b),

Р = 2 ( 1000 + 600 ),

Р = 3200 м.

Час знайдемо з формули

S = Vt ,

Де S = 3200м., V = 3 км/год.

Виконаємо перетворення

3 км/год = 3000 м. : 60 хв = 50 м/хв..,

Тоді

t = S : V,

t = 3200 : 50

t =64 хв =  1год 4хв.

Відповідь. 1год. 4хв.

III. Формування умінь і навичок.

1. Колективне розв’язування задач.

!. Ціну товару підвищили з 9,4 грн. До 12,5 грн. На скільки відсотків підвищилась ціна товару?

Розв’язання

Запишемо умову задачі у вигляді схеми:

9,4 грн. – 100%,

12,5 грн. – х %.

Складемо пропорцію:

9,4 : 12,5 = 100 : х.

9,4 х = 12,5 100,

9,4х = 1250,

х = 1250 : 9,4,

х 133 %/

133%  - 100 % = 33%/

Відповідь: Ціна товару підвищилася на 33 %..

2. На скільки відсотків  зменшиться час на поїздку, якщо швидкість збільшиться на 25%?

Розв’язання

Позначимо швидкість через  V. Якщо швидкість збільшити на 25%, то вона становитиме  V + 0,25 V = 1,25 V.

Запишемо умову задачі у вигляді схеми:

V – 100%,

1,25V – x %.

Відношення  швидкості і часу – обернено пропорційні величини. Складемо пропорцію:

V : 1,25 = x : 100,

1 : 1,25 = x  : 100.

1,25x  = 80.

100% - 80% = 20 %.

Відповідь.Час зменшиться на 20%.

2. Самостійне розв’язування задачі.

3. З усіх посаджених лип прийнялися 57, що становить 95. Скільки лип не прийнялися?

Розв’язання

Запишемо умову задачі у вигляді схеми:

57 лип – 95%,

х лип – 100%.

Складемо і розв’яжемо пропорцію:

57 : х = 95 : 100,

95х = 5700,

х = 5700 : 95,

х = 60.

60 – 57 = 3.

Відповідь. 3 липи не прийнялися.

IV.домашнє завдання. За підручником: № 88,98.,4