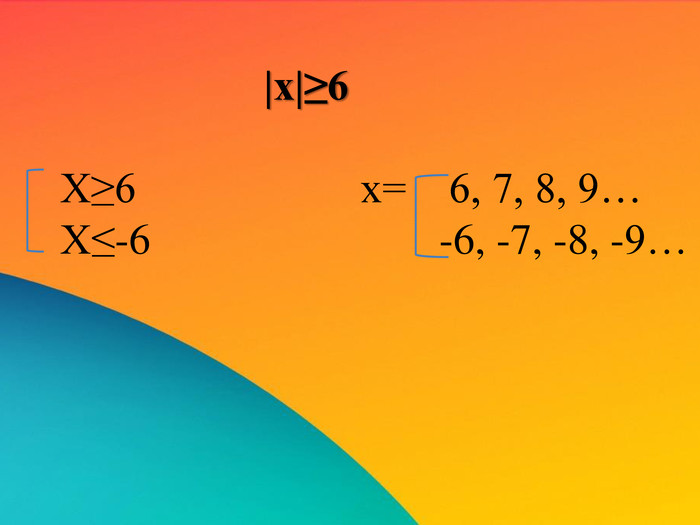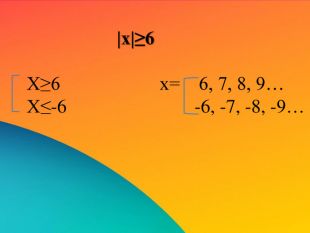Урок "Раціональні числа"

 

 

 

 

«Творча скарбничка - 2017»

 

Формування предметних компетентностей учнів у процесі навчання математики

Цикл уроків математики у 6 класі

на тему

«Раціональні числа»

 

Вчитель математики

ЗОШ І-ІІІ ст. №4

м. Жмеринки

Семенюк К. М.

Інформація про автора методичної розробки

1. Прізвище, імя, по батькові:    Семенюк Клавдія Михайлівна
2. Посада -    вчитель математики загальноосвітньої школи І-ІІІ ст.№4 м. Жмеринки
3. Кваліфікаційна категорія – спеціаліст вищої категорії, «Старший вчитель»

4. Рік народження - 1964

5. Поштова адреса: 23100,Вінницька обл.., м. Жмеринка, вул. Західна, 14

6. Адреса навчального закладу: 23100, Вінницька обл.., м. Жмеринка, вул. Київська, 3

7. Педагогічний стаж – 29 років

8. Досягнення:

    Публікація матеріалів на сайті «Шкільне життя»

• Подорож «Сторінками Червоної книги України» 6 клас. Математика (№255/2017)
• Гра-подорож «Господар свого дому». Розв’язування задач і вправ на всі дії з натуральними числами. 5 клас. Математика (№489/2017)

    На сайті «Методичний портал»

• Розв’язування задач з теми: «Відношення. Пропорції. Відсотки» 6 клас. Математика (№0000/54128)

Участь в учнівській науково-практичній конференції «До знань ми прагнемо». Керівник проектних робіт «Досягнення математичної науки в стародавній Греції», «Чудо відсотки».

9. Контактний телефон - +380682102658

10. Електронна пошта - semenyuk.klavdia.77@gmail.com 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

Значення математики як науки для формування цілісної, всебічно розвиненої особистості, яка має добре сформоване логічне та критичне мислення неможливо переоцінити. Проте на сьогоднішній день кількість учнів, які цікавляться, а значить, вивчають і мають високий рівень сформованості предметних математичних компетентностей є  недостатньою. Це стало викликом для вчителів математики, які повинні шукати принципово інші підходи до залучення учнів до ефективного освітнього процесу вивчення математики.

Дана розробка містить конспекти уроків з теми «Раціональні числа» відповідно до  оновленої програми з математики для 5-9 класів, затвердженої наказом МОН України № від 07.06.2017 р.

Цикл з 10 уроків передбачає формування предметних математичних компетенцій, ключових компетенцій та реалізацію наскрізних ліній навчальної програми. Зміст уроків забезпечує формування, засвоєння та використання знань, умінь і ставлень з усіх тем даного розділу. Розробки уроків характеризуються різноманітністю підходів, зокрема, у формах організації взаємодії вчителя з учнями та учнів між собою, методах та прийомах подачі, практикування та закріплення навчального матеріалу, способах унаочнення та використання ІКТ, «Родзинками» у процесі формування позитивної мотивації учнів до вивчення математики є використання ігрових прийомів та нестандартне, до певної міри загадкове для учнів формулювання теми уроків. Використання історичного матеріалу підвищує інтерес до вивчення математики, стимулює потяг до наукової творчості.

До кожного уроку підготовлено презентацію для супроводу уроку, яка дозволяє раціонально використовувати час вчителя на уроці в процесі переходу від одного виду діяльності до іншого.

Посібник буде корисним для вчителів математики, які викладають у 6 класі та студентів педагогічних навчальних закладів.

 

 

 

 

 

 

 

 

 

 

 

 

 

Формування предметних компетентностей учнів у процесі навчання математики.

Раціональні числа

цикл уроків, математика, 6 клас

Основна ціль: сформувати уміння розпізнавати додатні та від’ємні числа; уміння знаходити координати точок, зображених на координатній прямій, та позначати точки на координатній прямій за їх координатами; знання протилежних чисел; означення модуля числа, уміння знаходити модуль числа, розв’язувати найпростіші рівняння зі змінною під знаком модуля; уміння порівнювати раціональні числа.

Ключові поняття: додатні числа, від’ємні числа, координатна пряма, координата точки, протилежні числа, цілі числа, раціональні числа, модуль числа.

Ключові компетентності:

• уміння вчитися – уважно слухати вчителя, розвивати вміння запам’ятовувати, відтворювати інформацію, формувати вміння знаходити невідомі елементи.
• загальнокультурна – дотримуватися норм культури математичної мови, запису, культури спілкування, уміти формувати власні думки.
• здоров’язбережувальна – викликати позитивні емоції завдяки ігровим вправам.
• соціальну – розвивати вміння працювати в колективі, виховувати повагу до вчителя та однокласників.
• інформаційна–навчати учнів використовувати малюнки, таблиці, схеми  як джерела інформації.
• комунікативна– удосконалювати вміння дітей робити висновки за результатами своєї діяльності.
• емоційно-ціннісна – з’ясувати роль раціональних чисел у житті людини.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №1

Тема: Додатніта від’ємні числа. Число 0. «Подорож до країни РЧ»

Цілі:

навчальна: сформувати поняття додатних і від’ємних чисел, числа 0 як такого, що не є ні додатним, ні від’ємним; сформувати вміння читати, записувати, наводити приклади додатних та від’ємних чисел, розв’язувати вправи, які передбачають застосування поняття додатних і від’ємних чисел, розв’язувати вправи, які передбачають застосування поняття додатних і від’ємних чисел;

розвивальна: активізувати пізнавальну діяльність учнів, формувати вміння грамотно формулювати власні думки;

виховна: виховувати інтерес до вивчення математики, творче ставлення до справи.

Тип уроку: засвоєння нових знань і вмінь.

Очікувані результати:учень/учениця

• розпізнає додатні і від’ємні числа;
• розуміє, що число 0 не є ні додатним, ні від’ємним;
• вміє читати, записувати, наводити приклади додатних і від’ємних чисел;
• вміє застосовувати набуті знання під час розв’язування вправ;
• вміє працювати в парах.

Хід уроку

І. Організаційний момент

Ось і дзвоник пролунав

Для навчання час настав

На уроці ми працюємо під девізом

«Знати, мислити, вміти, діяти!»

ІІ. Формування нових знань.

Сьогодні подорож здійснимо ми в країну дива і краси, яка називається «РЧ». Спробуйте відгадати, що це за країна.

РЧ – нескінченної довжини

РЧ – бездоганної краси

Є тут цілі, є дробові

І звичайні, й десяткові,

Дивні числа з модулями

Є з «плюсами» й «мінусами»

Є тут дві великі групи

А між ними число нуль.

Учні відгадують, що це країна Раціональних чисел.

Та мушу попередити, що ця країна складається з двох регіонів.

«Плюсландія» та «Мінусландія», а розділяє ці регіони прикордонний стовп – число 0.

З регіоном «Плюсландія» і його жителями ми знайомі. Це числа, з якими ми працювали до сьогоднішнього уроку. Ці числа називаються додатними, тобто жителі «Плюсландії» - додатні числа. +2; 3; 100.

А як називаються жителі регіону «Мінусландія» ви дізнаєтесь, відгадавши загадку.

Нам ці числа треба знати

Щоб від двох п’ятсот відняти

З ними дія додавання

Це суцільне здивування

Все одно вони приємні –

Числа на ім’я… (від’ємні -10; -1)

Ви здивовані? Йдеться про числа, які вперше з’явилися в китайських математиків на початку нашого літочислення, а в ІV-V ст. індійські математики розвинули вчення про них, назвавши одні – майном, а інші боргом. Одні «чен» і позначали червоним кольором, а інші «фу» і позначали чорним кольором.

Творче д/з дізнатися які числа називаються майном  та боргом, «чен» і «фу».

А ми з’ясовуємо, де зустрічаються додатні і від’ємні числа у нашому житті.

1. Значення температури.
2. Розташування місцевості над рівнем океану.
3. Зміна грошей у касі.

 

Вкладник          Грошова операція

       1                             +500

       2                             -300

       3                             -100

       4                            +700

Виникає питання: Яким є число 0? Додатним чи від’ємним? Число 0 – ні додатне, ні від’ємне. Крім того, всі додатні числа разом із нулем називаються невід’ємними.

ІІІ. Формування вмінь.

Усні вправи.

1. Прочитати числа: 5; -9; -13; ; 0,4; -1,3; 0; -.

• Які з них додатні, які від’ємні?
• Чи є з-поміж них рівні між собою?
• Які числа невід’ємні?

2. За термометрами визначити температуру

Письмові вправи.

Робота в парах.

1. Установити на демонстраційному термометрі стовпчик так, щоб він показував температуру:

- 13°С              - 15°С

- 6°С                +4°С

2. Зобразіть схематично термометр, який показує - 7°С. Скільки градусів він показуватиме, якщо температура підвищиться на 4°С? (Зміниться на 3°С.)

(- 3; 0; - 6)

Інтерактивна вправа «Мозковий штурм»

Задача: Велосипедист проїхав біля кілометрового стовпа з написом 18 і продовжував їхати, в середньому зі швидкістю 12 км/год. Біля якого стовпа буде перебувати велосипедист через 0,5 год.? Через 1,5 год.? Через 2 год.?

Задача: Іра зайшла до ліфту дванадцяти поверхового будинку на сьомому поверсі. Проїхала 4 поверхи і вийшла. На якому поверсі вийшла Іра?

ІV. Підсумки уроку:

Як поділяються всі числа? Приклади.

Додатні; від’ємні;  недодатне і невід’ємне; 0.

Чи може виражатися від’ємним числом:

• кількість людей, які мешкають у будинку;
• довжина кімнати;
• кількість грошей;
• маса якого-небудь предмета?

Д/з: творче завдання, завдання за підручником.

 

 

 

 

 

 

 

 

 

 

 

 

Урок №2

Тема: Координатна пряма. Скарби історії «Стрічка часу»

Цілі:

навчальна: сформувати поняття координатної прямої, координати точки; будувати на координатній прямій точки за вказаними координатами.

розвивальна: сприяти розвитку уваги, розвивати творче мислення, вміння швидко орієнтуватися в нестандартних ситуаціях.

виховна: виховувати акуратність під час зображення рисунків, дисциплінованість.

Тип уроку: засвоєння нових знань і вмінь.

Очікувані результати: учень/учениця

• розуміє поняття координатної прямої, координати точки;
• визначає за готовими рисунками координати точок;
• будує координатну пряму, точки на координатній прямій за виданими координатами;

Хід уроку

І. Організаційний момент

Добрий день друзі, дівчата й хлоп’ята.

Я рада вас нині вітати.

Спочатку сідає краса, потім – сила.

Працюємо під девізом: «Навчатися можна тільки весело… Щоб переварити знання, потрібно ковтати їх з апетитом».

ІІ. Перевірка домашнього завдання

1. Творче завдання: Від’ємні числа утверджувались у математиці поступово. Від’ємними числами позначали борг, збиток, їх зображали червоним кольором. Від’ємні числа не не любили, їх називали «фу», що перекладається, як «чорний».

Додатними числами позначали майно, прибуток. Їм раділи і зображали червоним кольором.

2. Наявність письмового завдання, відповіді на запитання, які виникли в учнів при виконанні.
3. Гра «Так чи ні» - повторення теорії.

• число  12 додатне?                             - число -5 – додатне?
• число 0 – додатне?                             - число 0 – від’ємне?
• число  - від’ємне?                            - число -4 невід’ємне?
• число -3 –від’ємне?

4. Математичний диктант із самоперевіркою. 2 учні пишуть диктант на закритій частині відкидної дошки. Учні слухають текст і записують числа, додатні або від’ємні, залежно від умови.

• Найнижча точка рівнинної частини України знаходиться біля Куяльницького лиману, вона розташована на 5 м нижче від рівня океану.
• Рівень води в Азовському морі на 0,4 м нижчий від рівня Світового океану. Середня висота рівнинної частини України становить 175 м над рівнем океану.
• Найвища точка України – це гора Говерла, її висота становить 2061 над рівнем океану, а висота гори Берди, що на Прикарпатті, - 515 м над рівнем океану.

ІІІ. Формування мети і завдань уроку. Актуалізація опорних знань.

Загадка: На базарі їх не купиш,

               На городі не знайдеш

               Їх не зважиш на терезах

               І ціни не підбереш.

На цьому етапі уроку повторюємо, відтворюємо.

1. Ярий промінь називається координатним?
2. Якої довжини зручно вибрати одиничний відрізок, щоб на координатному промені позначити числа:

5; 2; 7; 3;                                                  0,4; 0,6; 0,7; 0,3;

; ; ; .

3. Знайдіть координати точок, зображених на рисунку:

 

 

 

 

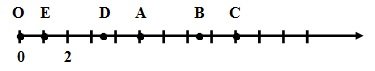
Де знаходяться точки Е, А, В, С, D по відношенню до 0? Якими числами є координати точок О, Е, А, В, С?

4. Позначте на координатному промені числа: 3; 5; 2,5; 1; -3; -2.

Під час виконання учні розуміють, що на координатному промені числа -3, -2 позначити неможливо. Виникає потреба «розширити» координатний промінь.

Завдання уроку – ознайомитись з поняттям координатної прямої.

ІV. Формування нових знань.

Ми подорожуємо країною «Раціональних чисел».

Всі мешканці цієї загадкової країни можна розмістити на прямій. Давайте спробуємо.

Згадаймо термометр – від’ємні, додатні числа. Як їх відокремити? (Відповіді учнів: Звичайно за допомогою нуля, бо ж нуль ні додатне, ні від’ємне число).

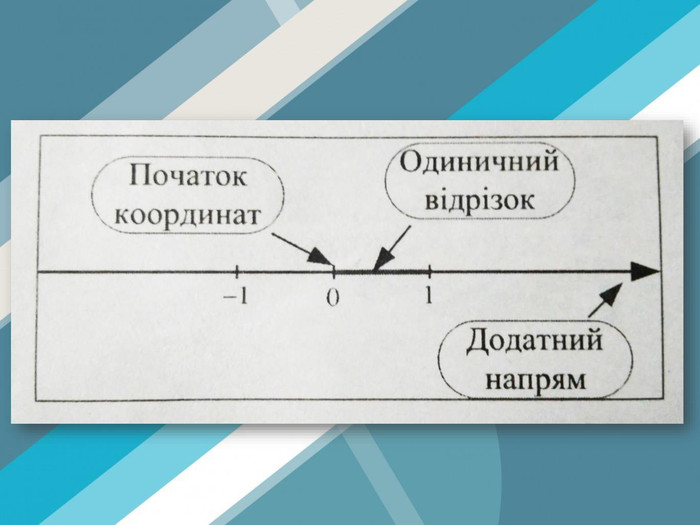
Так. Нуль – початок координат. А де розмістилися від нуля додатні числа?

Учні – праворуч, а від’ємні - ліворуч. У всіх чисел і додатних, і від’ємних – один і той самий одиничний відрізок.

Висновок: Що таке координатна пряма?

Учні: це пряма на якій є початок відліку, одиничний відрізок і напрям.

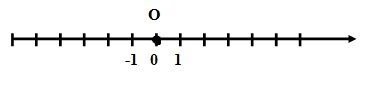
Діти, на яких уроках ви зустрічалися з координатною прямою?

Звичайно, на уроках історії. Там вона називалась «стрічка часу». За початок відліку християни беруть день народження Ісуса Христа (Різдво Христове) час після того дня – новою ерою, а до того – до нової ери.

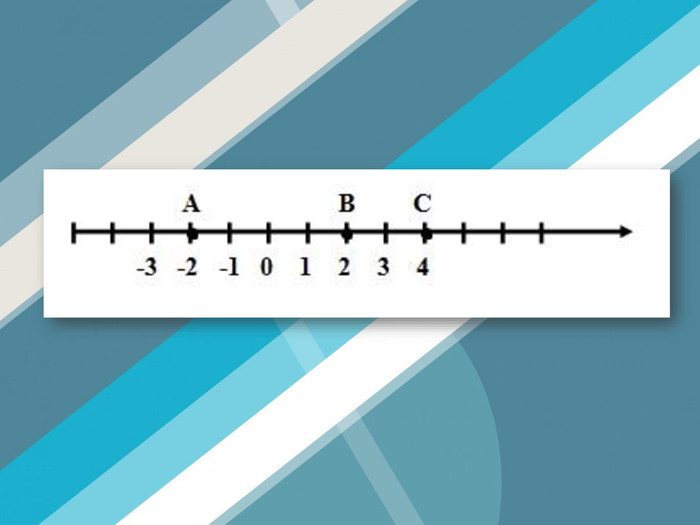
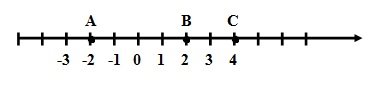Часто на координатній прямій поряд з числами записують букви, ними позначають точки на прямій, називають координатою точки.

 

 

 

V. Формування вмінь.

Усно:

Де відносно початку координат (праворуч чи ліворуч) розташовані точки:

А (6), В (-17), С (190), Е (-200).

Наведіть приклади двох точок, які:

• розташовані праворуч від початку координат;
• розташовані ліворуч від початку координат;
• розташовані по різні боки від початку координат.

Письмово:

• На координатній прямій позначено точки А (-2) і В (7). Знайти відстань між точками А і В в одиничних відрізках.
• Накреслити координатну пряму, позначити на ній точку А (-3). Позначити на прямій точку, віддалену від точки А:

а) у додатному напрямі на 6 одиниць;

б) у від’ємному напрямі на 4 одиниці;

в) на 6 одиниць.

Інтерактивна вправа «Мозковий штурм».

Задача: На координатній прямій позначено точки А, В, С, М, Р. Точка А розміщена праворуч від точки  С на 11 одиниць, точка М – ліворуч від точки А на 4 одиниці. Точка В віддалена від точки Р на 3 одиниці, а точка Р розміщена ліворуч від точки М на 9 одиниць. Які координати може мати точка В, якщо точка С має координату -7? В (-6) або В (-12).

VІ. Підсумок уроку

• Яку пряму називають координатною?
• Як на координатній прямій позначають додатний напрям?
• Яку координату має початок координат?

VІІ. Домашнє завдання

 

 

Урок №3

Тема: Протилежні числа. «Цікавий експеримент».

Цілі:

навчальна: сформувати поняття протилежних чисел, уміння їх знаходити та позначати на координатній прямій; сформувати вміння записувати число, протилежне поданому.

розвивальна: розвивати пам'ять, логічне мислення, уміння аналізувати й узагальнювати, творчі здібності.

виховна: виховувати уважність, спостережливість, відповідальність за результати своєї роботи.

Тип уроку: засвоєння нових знань і вмінь.

Очікувані результати:учень/учениця

• розпізнає протилежні числа, позначає їх на координатній прямій;
• вміє записувати число, протилежне поданому;

Хід уроку

І. Організаційний етап

У школі пролунав дзвінок

Розпочинаємо урок

Приготуйте зошит, книгу,

Вирівняйте гарно спину

Всі до мене поверніться

І хоч трішки усміхніться

ІІ. Перевірка домашнього завдання . Актуалізація опорних знань.

1. Наявність письмових вправ, та відповіді на питання, які виникли при виконанні.
2. Логічне: скільки точок з координатою 5 можна позначити на координатній прямій?
3. Математичний диктант (взаємоперевіркою). Варіант 1 (2); (2 учні біля дошки)

• Запишіть число «мінус чотири» (мінус шість);
• Як називається числа, перед якими стоїть знак « - »?
• Запишіть число, яке розташоване на відстані 4 одиниці праворуч (5 одиниць ліворуч) від нуля;
• Запишіть від’ємне (додатне) число, розташоване на відстані 7 (5) від нуля;
• Запишіть число, яке є ні додатним, ні від’ємним;
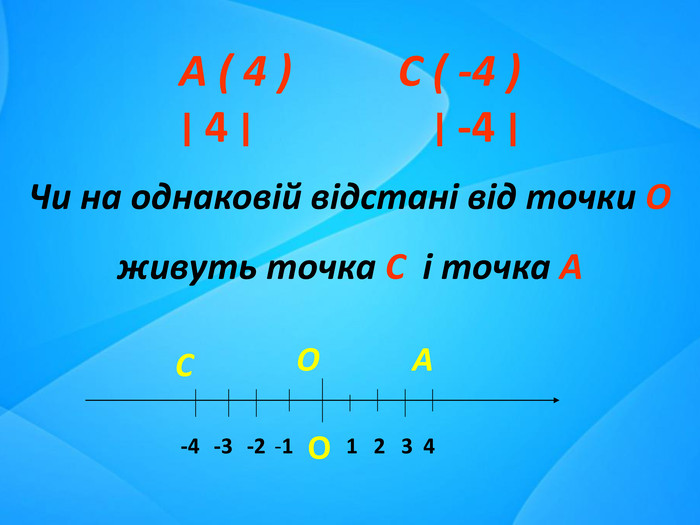
• Побудуйте на координатній прямій точки А (-3) і В (3) (С (-4) і D (4) ). Як вони розташовані відносно початку координатної?

ІІІ. Формулювання мети і завдань уроку.

Участь в «експерименті»

Побудувати координатну пряму, позначити на ній по дві точки, які розташовані на однаковій відстані від початку координат, записати координати цих точок.

Результат «експерименту». Усі учні дістали числа, які відрізняються тільки знаком. Ці числа мають спеціальну назву – протилежні.

Отже, завдання уроку – зрозуміти, які числа називають протилежними, навчитись розв’язувати задачі, які передбачають використання поняття протилежних чисел.

ІV. Засвоєння знань

Означення:Протилежними називаються числа, які однаково віддалені від початку координат, але в протилежних напрямках. Протилежні числа відрізняються лише знаками.

-7 і 7;       5 і -5;        і -

Число 0 протилежне саме собі.

Число, протилежне числа а, позначають –а.

а = -7, 8 то -а = 7, 8                      а = 8, 3 то -а = -8, 3

а = 0, то -а = 0                               - (-15) = 15

V. Формування вмінь.

Усно: Чи правильно, що

- (+13) = -13                   - (-8) = 8

- (-3,2) = 3,2                   - (+29) = 29

- (-12) = -12                    - (+7) = -7

Письмово:

Розв’язати рівняння:

-х = 530                   -х = -38              - (-х) = 9

Самостійно:

1. Заповнити порожні місця в таблиці:

х	3		5		0		-6	-10
-х		4		-2		-1

2. Поставити замість зірочки таке число, щоб утворилася правильна рівність:

-(-80) = *                 -(-247) = *

3,5 = -*                    8,2 = -*

VІ. Підсумок уроку

• Яке число протилежне самому собі?
• Чи існують два числа, які були б одночасно протилежними і взаємооберненими? Чому?
• Одного разу Вітя Верхоглядкін упродовж цілої години намагався відшукати два протилежні числа, які були б обидва від’ємні, але без успіху. Чому?

VІІ. Домашнє завдання

 

Урок №4

Тема: Цілі числа. Раціональні числа. «Знайомство з новими жителями».

Цілі:

навчальна: сформувати в учнів поняття цілих чисел, раціональних чисел; сформувати вміння розпізнавати ці числа, розв’язувати задачі, які передбачають використання цих понять.

розвивальна: активізувати пізнавальну діяльність учнів, розвивати пам'ять.

виховна: виховувати наполегливість у досягненні мети, упевненість у своїх силах, прищіплювати любов до математики.

Тип уроку: засвоєння нових знань.

Очікувані результати:учень/учениця

• розуміє поняття цілих чисел, раціональних чисел;
• розпізнає ці числа серед інших, наводить приклади;

Хід уроку

І. Організаційний етап

Починаємо знань вивчення новий урок.

Хай буде упевненим кожен ваш крок.

У навчанні бажаю вам старання.

І будуть правильно розв’язані завдання.

ІІ. Перевірка домашнього завдання

1. На зворотній частині дошки записано розвязки завдань, учні перевіряють їх, якщо є помилки, то виправляють.
2. Математичне лото «Хто найуважніший».

Учитель швидко називає числа, а учні повинні закреслювати числа, протилежні до названих у таблиці.

Вчитель: 7; 5; -14; 3; 13; -13; -7; -1; 14; 12; 1; -6; 11; 10; -15; -3; -4; 8.

 

Учні:

-6	7	15	3	-11	-8
13	-14	10	12	-4	-1
4	-3	-9	2	9	-13
-12	14	5	-2	-10	0
11	-7	8	6	-5	1

 

 

 

 

 

Вчитель: Порахуйте, скільки не закреслених чисел у вас залишилося? Отримали число 12.  Бажаю, щоб оцінка на уроці була у вас «12»!

ІІІ. Формулювання мети і завдань уроку

Проблемне запитання:

Як називають числа, записані в кожному з рядків:

1. 5; 27; 11; 109; 56; 1020; 981.
2. 7,7; ; 0,95; 2 ; ; 4,78.
3. -4; 9; 0; -15; 310; -243; -52; 506.
4. 64; -2,9; 9,7; - ; 6 ; -98?

Учні відповідають, що числа, записані в першому рядку – натуральні, в другому – дробові, а в третьому і четвертому – не знають.

Учитель повідомляє, що в третьому – цілі числа, а в четвертому – раціональні.

Завдання уроку – засвоїти поняття цілого і раціонального числа, навчитися пов’язувати задачі, які передбачають використання цих понять.

ІV. Засвоєння знань

Цілими числами називають:натуральні числа, їм протилежні та число нуль.

Приклад: 5; -5; 0; 2

Чи є цілими числа: -5,2; -; 5,2? – ні.

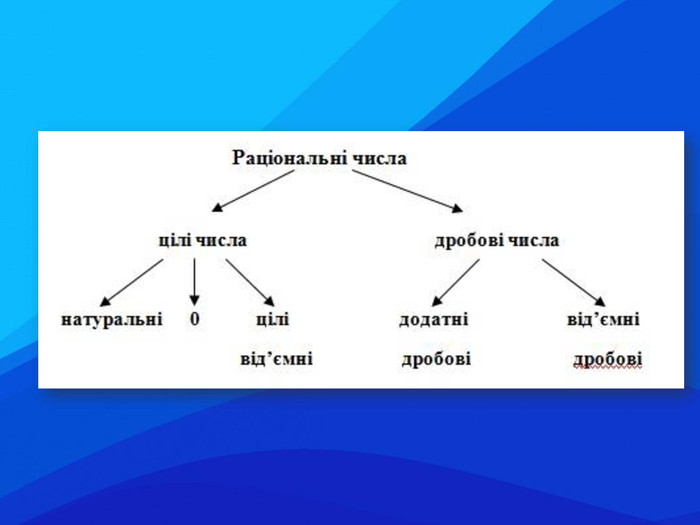
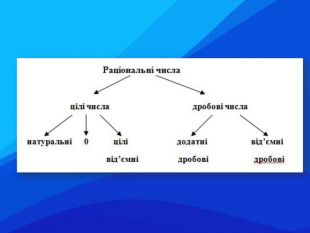
Раціональні числа

 

                                                        цілі числа                                       дробові числа

 

                                  натуральні       0            цілі                     додатні                      від’ємні

                                                                        від’ємні                 дробові                        дробові

Приклад: -5; -5,5; 2; 5.

V. Закріплення нових знань

1. Гра «Відгадай яке число».

На дошці в різних місцях прикріплені три таблички:

 

 

 

 

 

 

Учні записують в колонки під табличками числа, що відповідають назві таблички.

-7; -4; 0; 1 ; 3; 2,5; -6 ; 7; 5.

2. Які цілі числа розміщені на координатній прямій між числами:

-2 і 2;               -9 і -4;             -3 і 0;                -3,6 і 4,2

- і 3;               2 і 5 ;

На повторення:

3.  Запишіть числа:

Обернені числам: 12; ; 2 ; 0,6; -8,6; -2 ; 0.

4. Виконайте дії і знайдіть числа, протилежні й обернені до значень виразів.

.

VІ. Підсумок уроку

Запитання:

• Які числа називають цілими?
• Які числа називають раціональними?
• Навести приклади цілих чисел, раціональних чисел.

VІІ. Домашнє завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №5

Тема: Модуль числа «Загадкова величина»

Цілі:

навчальна: сформувати поняття модуля числа, уявлення про геометричний зміст модуля числа; сформувати вирази, що містять модуль, знаходити модуль числа, значення виразів, що містять числа під знаком модуля.

розвивальна: розвивати кмітливість, творчість, ініціативу, логічне мислення.

виховна: наполегливість у праці, віру у власні сили.

Тип уроку: засвоєння нових знань.

Очікувані результати:учень/учениця

• розуміє, що таке модуль числа;
• розв’язує вправи, що передбачають знаходження модуля числа;
• вміє читати і записувати вирази, що містять модуль.

Хід уроку

І. Організаційний момент

Прийом «Подаруй мені усмішку»

Девіз уроку:

Не просто слухати, а чути.

Не просто дивитися, а бачити.

Не просто відповідати, а міркувати.

Дружно і плідно працювати.

ІІ. Перевірка домашнього завдання

1. Наявність письмових вправ, відповіді на запитання, які виникли при виконанні.

2. Записати у відповідні стовпчики таблиці числа, які відповідають їм:

8; 0; -10; -12; ; 5,4; -612; -3,1; 2,91; -1001; 15 ; 256.

натуральні	цілі	додатні	не додатні	цілі від’ємні	дробові від’ємні

 

ІІІ. Формулювання мети і завдань уроку

Проблемна ситуація:

Знайти значення виразу:

Учні не розуміють цей запис. Учитель пояснює, що дві вертикальні риски поряд з числом означають, що потрібно розглядати не саме число, а його модуль.

Завдання уроку – дізнатися, що називають модулем числа, навчитись знаходити модуль числа, значення виразів, що містять числа під знаком модуля.

ІV. Актуалізація опорних знань

Задача: Знайти відстань від початку координат до точок координатної прямої:

А (-4)   В (4)  С (2)  Е (-2 )        О (0).

Запитання: Чи може шукана відстань бути від’ємним числом; нулем?

Як пов’язана шукана відстань з координатами точки? Чи може відстань від початку відліку до заданої точки дорівнювати координаті цієї точки?

Чи завжди відстань від початку відліку до поданої точки дорівнює координаті точки? У яких випадках це не так?

V. Засвоєння знань.

Ми з вами подорожуємо країною РЧ. П’ятикласники і учні молодших класів в цю країн не допускаються. Але й ті шестикласники, які не знайомі з координатною прямою, ризикують не потрапити до неї. Давайте пригадаємо, яка пряма називається координатною прямою (учні дають означення). Молодці! Допуск отримано.

І сьогодні ми будемо знайомитись з загадковим гарним жителем країни РЧ – Модулем.

Модуль – відстань від початку відліку до точки на координатній прямій.

Пройди вправо до числа 4. Отже, 4 по модулю дорівнює 4. Записують

Тепер пройди вліво 4 одиничних відрізків. Знайшли, це число -4. Отже, .

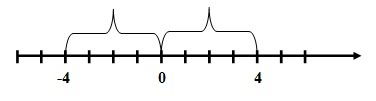
Як цікаво, модуль додатного числа – те саме число, і модуль від’ємного числа – число додатне, протилежне до від’ємного.

А чому дорівнює модуль нуля? Яка відстань від початку відліку до нуля?

Нуль – розмірковують діти.

Отже, .

Пам’ятка: ;

.

Однаковий модуль мають два протилежних числа.

Приклад: , тому х=3 або х=-3.

Гра «Так чи ні».

VІ. Осмислення нових знань.

Можна повернутися до проблемної ситуації і обчислити значення виразу:

=.

Усно:

Чи правильна рівність:

;              -

Письмово:

Знайдіть значення виразу:

;                                          ;

;                                     

.

Розв’яжіть рівняння:

VІІ. Підсумок уроку

1. Повторення основних понять.

2. Рефлексія:

- Чого навчилися на уроці?

- Чи досягли поставленої мети?

- Чи продуктивною була ваша робота на уроці?

VІІІ. Домашнє завдання

 

 

 

 

 

 

 

 

Урок №6

Тема: Модуль числа. Подорож Модуля до міст «Рівняння» та «Нерівності».

Цілі:

навчальна: удосконалити вміння застосовувати поняття модуля числа до розв’язування задач, найпростіших рівнянь і нерівностей, що містять знак модуля.

розвивальна: розвивати творче мислення, пізнавальні здібності учнів.

виховна: виховувати наполегливість у праці.

Тип уроку: удосконалення знань і вмінь.

Очікувані результати: учень/учениця

• застосовує поняття модуля числа до розв’язування найпростіших рівнянь, нерівностей, що містять знак модуля;

Хід уроку

І. Організаційний етап. Привітання. Підготовка класу до уроку.

ІІ. Перевірка домашнього завдання у формі фронтального опитування.

• Що називають модулем числа?
• Як позначають модуль?
• Чому дорівнює модуль додатного числа? Нуля?
• Чому дорівнює модуль від’ємного числа?
• Чи може модуль якого-небудь числа бути від’ємним числом?

Математичний диктант.

Варіант 1 (2); 2 учні працюють біля дошки.

• Запишіть рівність: модуль числа -5 дорівнює 5 (модуль числа 7 дорівнює 7). Чи правильна рівність, яку ви отримали?
• Чому дорівнює модуль числа ?
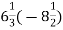• Чому дорівнює модуль числа 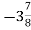(0)?
• Розв’яжіть рівняння (
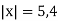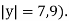
• Знайти значення виразу

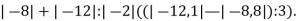
ІІІ. Формулювання мети і завдань уроку

Запитання: Чи існують задачі, де можна застосовувати поняття модуля?

Завдання уроку – дати відповідь на це запитання, навчитися розв’язувати задачі, які передбачають застосування поняття модуля числа.

ІV. Удосконалення знань

Пам’ятка! - відстань на координатній прямій від початку відліку до точки з координатою х.

Починаємо подорож у місто «Нерівність».

• Розв’язати в цілих числах нерівність .

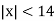Шукаємо такі цілі числа на координатній прямій, відстань від яких до початку відліку менша за 14 один. в. Це числа -13, -12, -11, -10, -9, -8, -7,-6,…0, 1, 2…13.

|х| < 14             

• Розв’язати в цілих числах нерівність

Шукаємо такі цілі числа на координатній прямій, відстань від яких до початку відліку більша або дорівнює 6 один.в.

                         х =   6,7,8, 9…

                              -6, -7, -8, -9…

Подорож до міста «Рівняння».

Розв’язати рівняння:

Інтерактивна вправа «Займи позицію».

Перед вами дві позиції «Так», «Ні».

Якщо згодний з написом на картці став під написом «Так», якщо ні – під написом «Ні».

Картки для гри:

 

 

 

 

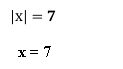
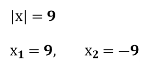
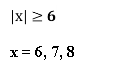
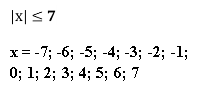
Висновок:

 

 

Означення і властивості модуля ми використовуємо для (відповіді учнів):

• Знаходження модулів числа;
• Розв’язування рівнянь ;
• Розв’язування нерівностей ;
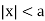• Відстань.

V. Підсумок уроку

Ігровий момент. Я задумав два протилежні числа. Поставте тільки одне запитання, щоб дізнатися ці два числа.

Скільки існує:

• Натуральних чисел;
• Цілих чисел;
• Цілих від’ємних чисел;
• Які задовольняють нерівність ?

VІ. Домашнє завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №7

Тема: Порівнянняраціональних чисел. «Суперечка чисел»

Цілі:

навчальна: домогтися засвоєння правила порівняння раціональних чисел; сформувати вміння розв’язувати задачі, які передбачають використання цього правила.

розвивальна: формувати вміння грамотно формулювати  власні думки, розвивати логічне й абстрактне мислення.

виховна: виховувати спостережливість, уважність, інтерес до математики.

Тип уроку: засвоєння нових знань і вмінь.

Очікувані результати: учень/учениця

• вміє порівнювати раціональні числа.

Хід уроку

І. Організаційний етап. Привітання, налаштування на роботу.

ІІ. Перевірка домашнього завдання.

Бліцопитування:

На дошці написано ціле від’ємне число -17. Учні швидко дають відповіді на «запитання», які вчитель ставить у короткій формі.

• Яке число?
• Назвіть його модуль;
• Його протилежне;
• Йому обернене;
• Число, що має менший модуль;
• Де число розташоване на координатній прямій?
• Чому дорівнює відстань від цього числа до початку відліку?
• Відстань між цим числом і йому протилежним?

ІІІ. Актуалізація опорних знань.

Самостійна робота

Група А (високий рівень)

1. Розв’язати рівняння:

2. Розв’язати в цілих числах нерівність:

Група Б (достатній рівень)

1. Обчислити значення виразу:

2. Розв’язати рівняння:

Група В (середній рівень)

1. Виконати дії:

2. Розв’яжіть рівняння:

ІІІ. Формування нових знань

Учитель: Якось два раціональних числа а і в, які уже давно мешкали на координатній прямій, посперечались, котре з них більше

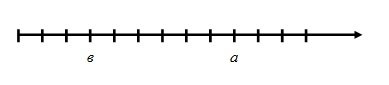
• Порівняй мої розміри, я вище від тебе. Отже, я більше, - сказало в.
• А я ширше від тебе, мій хвостик далі простягається. Тому я більше, - відповіло а.

Вони знаходили все нові й нові аргументи. Суперечка не стихала. Нарешті координатній прямій обридли ці сварки і вирішила вона покласти цьому край.

• Ви ніколи не дійдете згоди, бо не знаєте конституції нашої країни, країни РЧ.

Стаття 1. З двох чисел меншим вважається те, якому на координатній прямій відповідає точка, розміщена лівіше.

Стаття 2. З двох чисел більшим є те число, якому на координатній прямій відповідає точка, розміщена правіше.

• Правіше розміщено число а, тому ав.

Пам’ятка: Правіше – більше.

                  Лівіше – менше.

Числа а і в швидко заспокоїлись, вони добре знали, що закони потрібно виконувати.

Але інші раціональні числа розгубилися.

• А якщо нам потрібно буде порівнятися, а поруч не буде координатної прямої. Що ж тоді робити?

Координатна пряма і їх заспокоїла.

Є ще кілька законів. Є числа додатні, від’ємні, число нуль. Додатні числа розміщені правіше від від’ємних і від нуля, а нуль правіше від від’ємних.

Стаття 3. Будь-яке додатне число більше від будь-якого від’ємного і звичайно, від нуля.

Стаття 4. Будь-яке від’ємне число менше від нуля.

 Тут обізвалися від’ємні числа:

• Ну, а як з нами бути?

На що пряма їм відповіла:

• А давайте позначимо на прямій два від’ємних числа. Зліва маємо те, в якого більший модуль.

Стаття 5. З двох від’ємних чисел меншим є те, модуль якого більший.

З того часу в країні РЧ більше не виникало суперечок, яке з чисел більше, всі неухильно дотримувалися конституції.

ІV. Закріплення

Порівняти:

-2 і 4                    -3 і -1                     -8 і 0

7 і -9                   -10 і 0                     -9 і 2

-4 і 5                    -6 і 5                      -7 і -1

Розмістити в порядку зростання:

4; -7; 3; -6; 0; 2,1; -7,2; -6,8; 1,5

Яку цифру слід поставити замість зірочки, щоб утворилася правильна нерівність:

-2,403*-2,4034

V. Підсумок уроку

Заповнити порожні комірки таблиці:

Число	Більше за -3	Менше від 7	Більше за 0	Менше від 0	Більше за -1 але менше від 1
Додатне Від’ємне

 

VІ. Домашнє завдання

 

 

 

 

 

 

Урок №8

Тема: Порівнянняраціональних чисел.

Цілі:

навчальна: удосконалити вміння розв’язувати задачі, які передбачають порівняння раціональних чисел.

розвивальна: формувати вміння бачити закономірності, розвивати творчі здібності, кмітливість учнів

виховна: виховувати зосередженість, уважність, свідоме ставлення до навчання.

Тип уроку: удосконалення знань і вмінь.

Очікувані результати: учень/учениця

• розв’язує задачі, які передбачають порівняння раціональних чисел.

Хід уроку

І. Організаційний етап

У школі пролунав дзвінок

Розпочинаємо урок.

Доброго дня вам, діти!

Спочатку сідає краса, потім сила!

ІІ. Перевірка домашнього завдання

1. Наявність письмового завдання перевіряють відповідальні учні.

2. Тестові завдання:

1) Яка з числових нерівностей є правильною?

А.                                   Б.

В.                                       Г.

2) Серед чисел 10; -4; 0; -20 найбільшим є:

А. -20                                                Б. 10

В. 0                                                   Г. -4

3) Записати числа 0; -13; 5; -4 у порядку зростання:

А. -13; -4; 5; 0                                  Б. -13; -4; 0; 5

В. -4; -13; 0; 5                                  Г. 0; -13; -4; 5

ІІІ. Удосконалення знань.

Відомий вчений Іван Павлов (ХІХ ст..) говорив: «Ніколи не беріться за наступне, не вивчивши попереднього».

На уроці ми закріпимо отримані знання, застосовуватимо їх при розв’язуванні вправ і задач.

Усно:

• Назвати три числа, які задовольняють нерівність
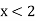
• Назвіть три числа, які задовольняють нерівність
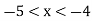
• Назвіть три числа, які задовольняють нерівність

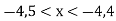
Письмово:

• Між якими сусідніми цілими числами стоїть число:

-2,73;             -9,5;            0,63;              0,87

Відповідь запишіть у вигляді подвійної нерівності.

• Запишіть у вигляді нерівності речення:

-4,3 – від’ємне число;                               х – від’ємне число;

2,71 – додатне число;                                у – додатне число.

Самостійна робота

Група А (високий рівень)

1. Знайти всі цілі значення у, при яких є правильною нерівність:

2. Яку цифру можна поставити замість зірочки, щоб утворилась правильна нерівність:

3. Знайти найбільше ціле значення х, при якому є правильною нерівність .

Група Б (достатній рівень)

1. Записати в порядку зростання числа:

-2,4; 56; -4; -100; 32.

2. Між якими сусідніми цілими числами лежить число:

а) -9,36                  б) -0,8

Відповідь записати у вигляді подвійної нерівності.

3. Знайти найбільше ціле число, при якому є правильною нерівність:

Група В (середній рівень)

1. Порівняти числа:

-14 і 11                             0 і 13

-40 і 30                            -1,5 і 7,3

2. Поставити замість * таку цифру, щоб була правильною нерівність

ІV. Підсумок уроку

Фронтальне опитування

1. Яке число більше:

1) додатне чи від’ємне;

2) додатне чи 0;

3) від’ємне чи 0;

4) а чи в, якщо а і в – від’ємні і ?

2. Відомо, що Назвіть числа в порядку їх розташування на координатній прямій зліва направо.

V. Домашнє завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №9

Тема: Розв’язування задач

Цілі:

навчальна: узагальнити та систематизувати знання учнів з теми «Раціональні числа. Порівняння раціональних чисел».

розвивальна: формувати вміння узагальнювати та робити висновки, розвивати та робити висновки, розвивати творче мислення і винахідливість під час розв’язування нестандартних задач.

виховна: виховувати дисциплінованість, інтерес до математики.

Очікувані результати: учень/учениця

• впевнено використовує числа зі знаком «+» і зі знаком «-»;
• орієнтується на  координатній прямій, будує точки із заданими координатами;
•  розв’язує задачі із застосуванням чисел різних груп, протилежних чисел, модуля числа;
• усвідомлює важливість цієї теми для себепри вивчення математики

Хід уроку

Перша умова, якої потрібно

дотримуватися в математиці – це

бути точним, друга – бути чітким

і наскільки можливо, - простим.

Л. Карно

І. Організаційний етап

Ось і дзвоник дав сигнал,

Працювати час настав

Тож і ми часу не гаймо,

Працювати починаймо.

ІІ. Актуалізація опорних знань учнів

Учні по черзі ставлять один одному запитання:

• Які числа називають додатними?
• Які числа називають від’ємними?
• Яке число є ані від’ємним, ані додатним?
• Які числа називають протилежними?
• Які числа називають натуральними?
• Які числа називають цілими?
• Які числа називають раціональними?
• Що називається модулем числа?
• Як порівняти від’ємне число з нулем?
• Як порівняти додатне число з від’ємним?
• Як порівняти два від’ємних числа?
• Що таке координатна пряма?

ІІІ. Розв’язування вправ

1. У якому році додатні та від’ємні числа отримали геометричне тлумачення ви дізнаєтесь виконавши таке завдання:

На термометрі -2°С. Яку температуру показуватиме термометр, якщо стовпчик ртуті

• Підніметься на 18°С;
• Опуститься на 13°С;
• Підніметься на 4°С. (1637)

2. Кімнатний термометр завдовжки майже такий, як той, яким міряють температуру людям. Чи звернули ви увагу, скільки градусів розміщується на тому й другому?

- на кімнатному майже 50°С від -5°С до +45

- на медичному тільки 8° від 34,5°С до 42,5°С

3. Яке число записане на географічній карті, якщо воно означає, що найбільша глибина Азовського моря 12 м?     (-12) Це нижче від рівня океану.

4. Білка сидить на дереві в т. М(4), дятел – у т. Р(-3). Яка відстань від дятла до білки? Хто з них сидить далі від дупла, яке є початком відліку?

5. Трикутний прапорець розміщений у точці х координатою -2, а прямокутний у точці з координатою +2. Знайти й позначити початок відліку та одиничний відрізок. Записати координати точок В, С, К, D.

С(-4)         В(-2)                К(0)             D(1,5)

 

 

 

 

 

6. Розмістіть числа в порядку зростання і ви дізнаєтесь прізвище видатного вченого, який увів знаки «+» і «-» для позначення додатних і від’ємних чисел:

-25	-438		412	-482	-12
К	Е	Р	Т	Д	А

 

7. Число, яке не має знака?

8. Дано числа 6; -9; 5,25; ; 507; 9; -2,6; 1,125; 0; -207; . Які з даних чисел є натуральними? Цілими? Дробовими? Додатними? Від’ємними? Знайти модулі цих чисел. Які з даних чисел мають рівні модулі? Чому? Розмістити числа в порядку зростання.

ІV. Підсумок уроку

Ми з вами познайомилися з жителями країни «Раціональні числа».

Живуть всі у злагоді в казковій державі.

Разом роблять корисні справи –

допомагають розв’язувати задачі та вправи.

Служать вірно людям не одне століття.

І вдячні математикам за їхні відкриття

V. Домашнє завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №10

Тема. Контрольна робота.

Цілі:

навчальна: перевірити рівень засвоєння знань з теми «Раціональні числа. Порівняння раціональних чисел»;

розвивальна: розвивати вміння логічно мислити, правильно висловлювати свої думки в письмовому вигляді;

виховна: виховувати дисциплінованість, самостійність, відповідальність.

Тип уроку: контроль знань і вмінь.

Хід уроку

І. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу. Доцільно нагадати учням правила поведінки під час проведення контрольної роботи. На цьому етапі уроку можна нагадати учням критерії оцінювання контрольної роботи.

II. Перевіркадомашнього завдання

Учитель перевіряє зошити з виконаною домашньою контрольною роботою.

III. Формулювання мети і завдань уроку

Учитель наголошує, що метою контрольної роботи є демонстрування учнями своїх навчальних досягнень:

уміння розпізнавати додатні та від’ємні числа;

уміння знаходити координати точок, зображених на координатній прямій, та позначати точки на координатній прямій за їх координатами;

знання означення протилежних чисел;

знання означення модуля числа, уміння знаходити модуль числа, розв’язувати найпростіші рівняння зі змінною під знаком модуля;

уміння порівнювати раціональні числа.

IV. Текст контрольної роботи

Варіант 1

1. Укажіть кількість від’ємних цілих чисел з-поміж поданих:

А	Б	В	Г
П’ять	Шість	Три	Два

 

2. Розв’язком якого з наведених рівнянь є число 4?

А	Б	В	Г
–х=–4	–х=4	–х=–(–4)	Будь-якого з наведених

 

3. Яке з наведених чисел розташоване на координатній прямій між числами –5 і –2?

А	Б	В	Г
–1	0	–3	–6

 

4. Яке з наведених рівнянь не має розв’язків?

А	Б	В	Г
|х| = –6,8		|х| = 0	|х| = 0,01

 

5. Яке з чисел на координатній прямій розташоване ліворуч від решти наведених?

А	Б	В	Г
–6,05	–6,151	–6,054	–6,155

6. Яка з наведених нерівностей неправильна?

А	Б	В	Г
–0,28 >–0,42	–101>–100	0,2>–210,2

7. Позначте на координатній прямій точки А(–2) і В(6). У якому напрямку і на скільки одиниць потрібно перемістити точку В, щоб дістати точку С, координата якої протилежна координаті точки А?

8. Розв’яжіть рівняння |х| = |5| + |–7|.

9. Позначте на координатній прямій усі розв’язки нерівності Укажіть усі цілі розв’язки цієї нерівності.

Варіант 2

1. Укажіть кількість додатних цілих чисел з-поміж поданих: –4; 0; 7;–8,1; –11; 17; 0,9;–70.

А	Б	В	Г
Одне	Три	Два	Чотири

2. Розв’язком якого з наведених рівнянь є число 2?

А	Б	В	Г
–х = –(–2)	–х = –2	–х = 2	Будь-якого з наведених

 

3. Яке з наведених чисел розташоване на координатній прямій між числами –4 і –1?

А	Б	В	Г
–2	–5	0	1

 

4. Яке з наведених рівнянь не має розв’язків?

А	Б	В	Г
	|х|  = –4	|х| = 0,02	|х|  = 50

 

5. Яке з чисел на координатній прямій розташоване праворуч від решти наведених?

А	Б	В	Г
–3,03	–3,103	–3,031	–3,133

 

6. Яка з наведених нерівностей неправильна?

А	Б	В	Г
–0,45 >–0,5	–202<–200	0,01>–1000,1

 

7. Позначте на координатній прямій точки А(3) і В(–5). У якому напрямку і на скільки одиниць потрібно перемістити точку В, щоб дістати точку С, координата якої протилежна координаті точки А?

8. Розв’яжіть рівняння |x| = |–12|–|3|.

9. Позначте на координатній прямій усі розв’язки нерівності |x|  < 3. Укажіть усі цілі розв’язки цієї нерівності.

Відповіді

Варіант 1

1	2	3	4	5	6
Г	А	В	А	Г	Б

7. Ліворуч на 4 одиниці.

8. –12 і 12.

9. –2; –1; 0; 1; 2.

Варіант 2

1	2	3	4	5	6
В	Б	А	Б	А	Г

7. Праворуч на 2 одиниці.

8. –9 і 9.

9. –2; –1; 0; 1; 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаної літератури

1. Навчальна програма «Математика. 5-9 класи» (затверджена наказом МОН України від 07.06.2017 р. №408)

2. С.П. Бабенко. Усі уроки математики. 6 клас. Посібник для вчителя. Видавництво «Основа», 2014, 300с

2. Дмитренко О., «Дії з раціональними числами» (Газета «Математика» №20, 2016, с18-20)

3. Сивовол Л., «Додавання від’ємних чисел» (Газета «Математика» №11, 2012, с19-22)