Урок "Розв'язання квадратних нерівностей"

Тема уроку: Розв’язування квадратних нерівностей

Тип уроку: Урок вивчення нового матеріалу.

Мета уроку: Формувати поняття алгоритму розв’язування квадратних нерівностей, формувати навички застосування властивостей нерівностей,

розвивати навички  самостійної роботи, навички логічного мислення, монологічного мовлення, формувати культуру математичного спілкування.

«Алгебра » 9 клас підручник (автори: А.Г. Мерзляк, В.Б. Полонський, М.С. Якір), Пам'ятки з алгоритмом рішення нерівностей другого ступеня, комп'ютер, мультимедійний проектор, екран.

ХІД УРОКУ

I етап. Організаційний момент.

II етап. Пояснення нового матеріалу (Додаток 1)

Учитель: Вивчення нового матеріалу ми почнемо з поняття нерівності другого ступеня.

Завдання 1. Які з нерівностей ви б назвали нерівностями другого ступеня:

1) 6х² - 13х> 0;  2) x² - 3x - 14> 0;   3) (5 + x) (x - 4)> 7;

4); х-3≤12х+8;     5) х² =6;       6) х³ ≥8;

7) 8x²> 0; 8) (x - 5) 2 - 25> 0; 9) x (x - 9) - x2> 0?

- Тепер давайте сформулюємо визначення нерівності другого ступеня:

Визначення: Нерівність, ліва частина якого є многочлен другого ступеня, а права - нуль, називається нерівністю другого ступеня.

Всі квадратні нерівності можуть бути приведені до одного з наступних видів:

1) ах² + bx + c> 0;

2) ах² + bx + c <0;

3) ах² + bx + c≥ 0;

4) ах² + bx + c ≤0.

Завдання 2. Які з чисел є розв’язками нерівності?

- До квадратних нерівностей нас наводять такі завдання.

Завдання 1. Планується купити прямокутний килим, який буде примикати до стіни спортивної зали. Заготовленого матеріалу вистачить на довжину 20м. Якими повинні бути довжина і ширина килиму, щоб він мав площу не менше: 1) 48 м²; 2) 50 м².

- Обговоримо виконання цього завдання.

Якщо за х м прийняти довжину сторони килима, що примикає до стіни, то розв’язання задачі зведеться до вирішення нерівностей:

1) (20 - 2х) х> 48;

2) (20 - 2х) х> 50.

Використовуючи перетворення, ці нерівності можна привести до таких нерівностей другого ступеня:

1) х² - 10х + 24 <0;        2) х² - 10х + 25 <0.

Спробуємо знайти спосіб вирішення квадратних нерівностей, що використовує властивості квадратичної функції.

Учні намагаються запропонувати такий спосіб. Якщо ідей не виникає, то вчитель пропонує виконати ще одне завдання.

Завдання 2. На рисунку  дано графіки квадратичних функцій. Аналізуючи ці графіки , заповніть таблицю.

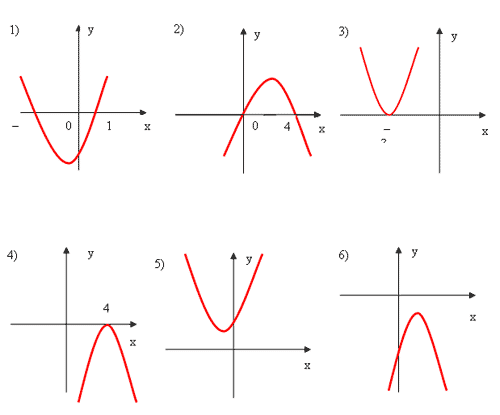
Рис. 1

Вчитель:  Тепер нам належить вирішити нерівність – х² + 8x - 12> 0. Яка інформація про квадратичну функцію може виявитися при цьому корисною:

знак коефіцієнта а;

знак дискримінанта D квадратного тричлена;

напрямок гілок параболи;

перетин параболи з осями координат;

 координати вершини параболи;

приблизне розташування параболи?

Чи обов'язково для вирішення нерівності будувати графік відповідної квадратичної функції? Якщо так, то з якою точністю виконувати побудову?

Далі розглядаються різні варіанти нерівностей з докладним рішенням і записом в зошиті (або довідники). (Додаток 1, див. презентацію)

Завдання:

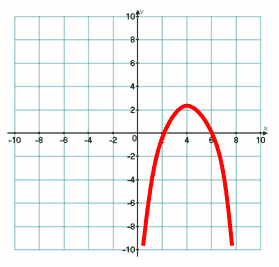
1)- х² + 8х - 12> 0.

 Розв’язання:   Нехай у = - х² + 8х - 12. а = - 1, а <0.

Гілки параболи спрямовані вниз.

- х² + 8х - 12 = 0; D = 64 - 4 (- 1) (- 12) = 16  , D> 0 x₁ = 6; x₂ = 2.

Схематично будуємо графік функції.

Відповідь: хє (2; 6).

2)  - х2 + 8х - 12? 0.    Відповідь: [2; 6].

3)  - х2 + 8х - 12 <0.    Відповідь: (-; 2) (6; +).

4)  - х2 + 8х - 12? 0.    Відповідь: (-; 2] [6; +).

5)   x2 - 8x + 12> 0.      Відповідь: (-; 2) (6; +).

6)   x2 - 8x + 12? 0.       Відповідь: (-; 2] [6; +).

7)   х2 - 4х + 4> 0.        Відповідь: (-; 2) (2; +).

8)   х2 - 4х + 4? 0.         Відповідь: (-; +).

9)    х2 - 4х + 4 <0.        Відповідь: немає розв’язків.

10)   х2 - 4х + 4? 0.       Відповідь: 2

11)  х2 - 4х + 5> 0.       Відповідь: (-; +).

12)  х2 - 4х + 5 <0.       Відповідь: немає рішень.

Учитель: Тепер давайте спробуємо сформулювати алгоритм  розв’язання нерівностей другого ступеня, заснований на властивостях квадратичної функції.

Після відповідей учнів вчитель пропонує порівняти їх з готовим алгоритмом, який лежить у кожного на парті (Додаток 2).

III етап. Засвоєння нових знань.  На цьому етапі учням пропонується самостійно вирішити кілька нерівностей. 1. 2. 3. 4. Перевірка рішення проводиться за готовими відповідями (презентація, слайди). Для найбільш підготовлених учнів пропонується наступне завдання:

 Знайти область визначення функції.

IV етап. Домашнє завдання §2.12, № 12.4, 12.6 (парні).

Література: Гельфман Є.Г., Бухтяк М.С. та ін. Квадратична функція: навчальний посібник з математики для 9 класу.