Презентація до уроку "Показникові рівняння та нерівності"
Про матеріал
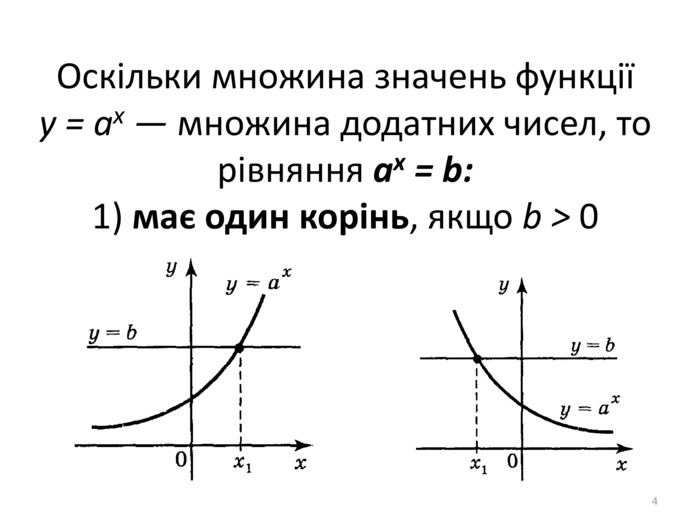
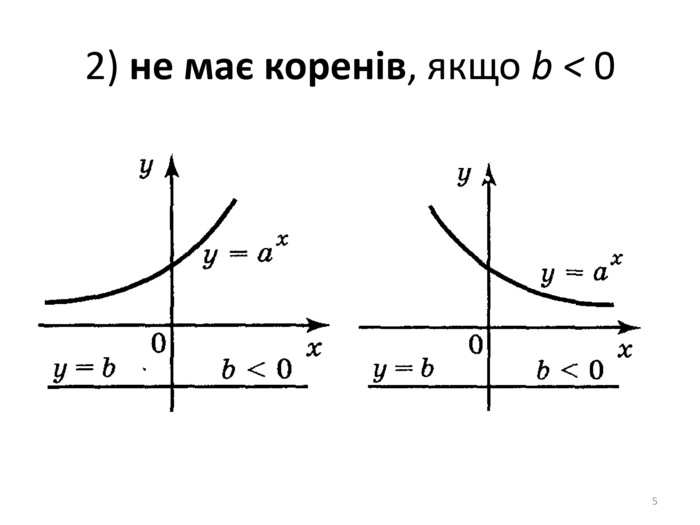
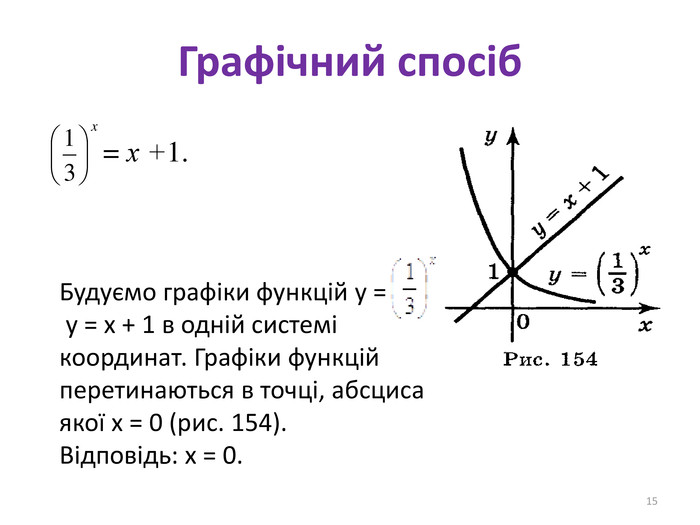
Презентація містить матеріал для проведення уроку з алгебри в 11 класі "Показникові рівняння та нерівності". Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



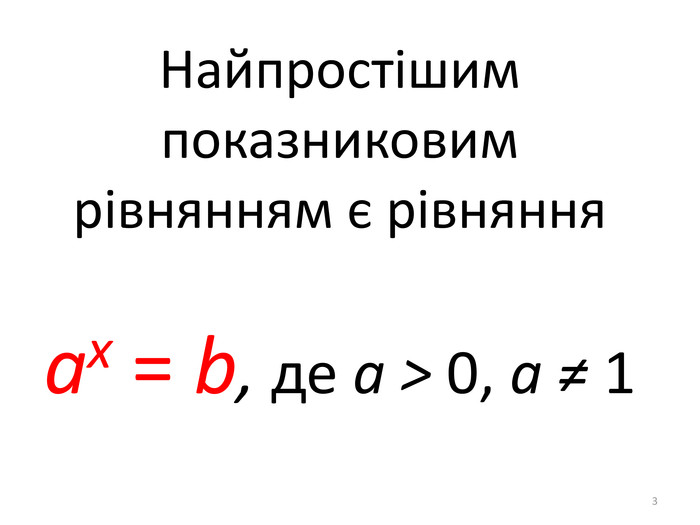

































-

Скоробогатих Оксана Богданівна
21.09.2025 в 15:41
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Семеняк Оксана Григорівна
22.01.2024 в 09:43
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Кравченко Лілія
16.10.2022 в 14:33
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Свільонок Олена Михайлівна
20.09.2022 в 20:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Наумова Катерина Олександрівна
08.09.2022 в 10:57
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука