Урок "Розв’язування рівнянь методом заміни змінної"

УРОК №

Тема: «Розв’язування рівнянь методом заміни змінної».

Мета: ознайомити учнів з означенням біквадратного рівняння та способом його розв’язання, дослідити кількість коренів біквадратного рівняння, скласти алгоритм розв’язування біквадратних рівнянь; формувати вмін­ня учнів виділяти біквадратні рівняння серед інших рівнянь; розвивати математичне мовлення та логічне мислення, інтерес до предмета математики; виховувати акуратність під час виконання записів.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: проектор, мультимедійна презентація.

Хід уроку

І. Організаційний момент (привітання, …).

ІІ. Перевірка домашнього завдання. Актуалізація опорних знань.

Минулого уроку ви отримали таке домашнє завдання:

1.          Повторити: означення квадратного рівняння, види квадратних рівнянь, формули дискримінанта та коренів квадратного рівняння;
2.          виконати такі завдання: 

1. Запропоновані рівняння розділити на групи (повні, неповні), розв’язати їх:

а)  2х²- 3х -5 =0                                                         г)  8х²=0

б)  х²+ х – 5=0                                                           д) 3х²-10х+8=0

в)  4х²+5х=0                                                               е) 3х²- 21х=0

2. Визначити коефіцієнти даних квадратних рівнянь:

6х²  – х  + 4  = 0

12х  -  х² +  7  =0

8 + 5х² = 0

х – 6х² = 0

- х + х² = 15

3. Скласти квадратні рівняння з такими коефіцієнтами:

а=6,в=7, с=-1

а=-1,в=-1, с=3

а=4,в=6, с=-2

4. Розв’язати рівняння:

 

 

 

Зараз ми перевіримо наскільки ви справилися з домашнім завданням.

Отже, «Бліц - опитування».

 Бліц-опитування

1. Яке рівняння називається квадратним?

ах²+вх+с=0

2. Які існують види квадратних рівнянь?

     (повні, неповні, зведені)

3. Як називаються числа   а, в, с?

а – старший коефіцієнт,  в – другий коефіцієнт , с – вільний член

4. Що означає розв’язати рівняння?

Розв’язати рівняння – знайти всі його корені, або показати, що їх немає.

5. Від чого залежить кількість коренів квадратного рівняння?

Від дискримінанта.

6. Як знайти дискримінант?

D=в²- 4 ас.

7. Яким чином кількість коренів залежить від дискримінанта?

               D0, 2 корені,             D0, 1 корінь,                D0, немає   розв’язків

8. Як розв’язати рівняння такого виду х²=а?

Якщо а=0,  то х=0.

Якщо а<0, немає розв’язків.

Якщо а>0, то  х₁= а,  х₂=-а.

 Далі  - «Інтелектуальна розминка»

№ 1

На екрані записані рівняння:

а)  2х²- 3х -5 =0                                                         г)  8х²=0

б)  х²+ х – 5=0                                                           д) 3х²-10х+8=0

в)  4х²+5х=0                                                               е) 3х²- 21х=0

Вдома ви повинні були розділити дані рівняння на групи (повні, неповні рівняння) та розв’язати їх.

Які з даних рівнянь є повними квадратними рівняннями?

( перевірити корені повних квадратних рівнянь)

Якими будуть інші три рівняння?

1. 2,5; -1
2. 
3. 

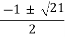
№ 2

Визначте коефіцієнти квадратного рівняння:

1	6х²  – х  + 4  = 0	а = 6,	в = -1,	с = 4,
2	12х  -  х² +  7  =0	а = -1,	в = 12,	с = 7,
3	8 + 5х² = 0	а = 5,	в = 0,	с = 8,
4	х – 6х² = 0,	а = -6,	в = 1,	с = 0,
5	- х + х² = 15	а = 1,	в = -1,	с = -15

№ 3

 Складіть квадратні рівняння:

1. а=6,в=7, с=-1
2. а=-1,в=-1, с=3
3. а=4,в=6, с=-2

1. 6x²+7x-1=0
2. -x²-x+3=0
3. 4x²+6x-2=0

№ 4

 Розв’яжіть:

 

 

 

№ 5

 Знайдіть помилку:

(х²)³=х⁵

(х²)²=х⁴

Все те, що ми з вами повторили, знадобиться під час вивчення нової теми.

ІІІ. Формулювання мети і завдань уроку.

 Сьогодні на уроці ми здійснимо подорож по країні «Математика», побуваємо в місті «Рівнянь», і від того наскільки ви будете уважними, як правильно виконаєте всі завдання, буде залежати наскільки вдало завершиться наша подорож. Адже рівняння – одне з найважливіших понять математики. І сьогодні ми з вами продовжимо серію уроків по розв’язуванню рівнянь, які зводяться до квадратних. Ви вже знаєте, що багато рівнянь в математиці за допомогою рівносильних перетворень зводяться саме до квадратних рівнянь. І одним із способів розв’язання таких рівнянь є спосіб заміни змінної. (слайд) А який тип рівнянь ми будемо розв’язувати використовуючи цей спосіб, ви дізнаєтесь, давши відповіді на запитання  математичного кросворда. Отже,1 станція нашої подорожі – станція «Інтелектуальна».

1. Третій степінь числа. (Куб) 
2. Вираз 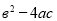  . (Дискримінант) 
3. Значення змінної, яке перетворює рівняння в правильну рівність. (Корінь) 
4. Рівняння, які мають однакові корні. (Рівносильні) 
5. Другий степінь числа. (Квадрат) 
6. Квадратне рівняння, у якого старший коефіцієнт дорівнює одиниці. (Зведене) 
7. Многочлен в правій частині рівняння. (Тричлен) 
8. Рівність, яка містить числа і змінні. (Формула) 
9. Французький математик. (Вієт) 
10. Числовий множник. (Коефіцієнт) 
11. Один з видів квадратного рівняння. (Неповне) 

Префікс «бі» в слові «біквадратне» означає два або двічі. Квадратні рівняння – це рівняння другого степеня. Біквадратні – двічі другого степеня. Як ви думаєте, біквадратні рівняння це рівняння якого степеня? (Четвертого)

Отже, сьогодні на уроці ми розглянемо застосування способу заміни змінних для розв’язання біквадратних рівнянь. Тема нашого уроку: «Розв’язування біквадратних рівнянь».

І завдання нашого уроку:

• використовуючи означення біквадратного рівняння, навчитися виділяти даний тип рівнянь серед інших рівнянь;
• розглянути на прикладах спосіб розв’язання біквадратних рівнянь;
• дослідити кількість коренів біквадратного рівняння;
• скласти алгоритм розв’язування біквадратних рівнянь.

ІV. Засвоєння нових знань і вмінь.

 Друга  станція на нашому шляху -  «Історична» (доповідь 1 учня)

В проблему розв’язання рівнянь 3-го і 4-го степеня великий  вклад зробили італійські математики 16 століття НіколоТарталья, Антоніо Фіоре, Джероламо Кардано та ін. Наприкінці 1534 року Тарталья одержав виклик на математичний турнір від Антоніо Фіоре — учня відомого професора математики Болонського університету Сципіона дель Ферро. Нікколо дізнався, що Фіоре володіє секретом розв'язання багатьох рівнянь, який йому повідомив Ферро. Шляхом титанічних зусиль Тартальї за кілька днів до диспуту теж вдалося знайти спосіб розв'язання такого рівняння.

Двобій відбувся 12 лютого 1535 року. Кожному із супротивників треба було розв'язати по 30 задач. За дві години Тарталья впорався з усіма задачами, запропонованими йому Фіоре, а той не розв'язав жодної задачі свого противника. Перемога була повною, вчений прославився на всю Італію і отримав кафедру математики у Вероні.

Своїм методом розв'язування рівняння Тарталья поділився з відомим ученим Джироламо Кардано, що був одночасно математиком і механіком, лікарем і алхіміком, хіромантом і особистим астрологом римського папи, взявши з того слово ніколи не публікувати повідомлений йому метод розв'язання. Але через шість років Кардано порушив свою клятву — він видав трактат «Велике мистецтво, або про правила алгебри» (1545), де виклав алгоритми розв'язування рівнянь третього і четвертого степеня.             

(доповнити відповідь)

Отже, і ми з вами переходимо до розгляду рівняння четвертого степеня – біквадратного рівняння і наступна зупинка - «Місто рівнянь».

Рівняння виду ах⁴+bх²+с=0, де а, в, с – задані числа, причому а0,

х – змінна, називається біквадратним.

 Наприклад,   х⁴-2х²- 8=0 (написати на дошці)

Спробуйте скласти і записати в зошиті по 2 біквадратні рівняння, використовуючи різні значення коефіцієнтів.

Серед представлених рівнянь виберіть біквадратні:

х⁴+7х²+12=0

2х⁴-2х³ +9х² +5х+ 4=0

х⁴-3х²+ 2=0

х³-2х²- 8=0

2х⁴-9х²+ 4=0

Для розв’язання біквадратних рівнянь використовується спосіб, який називається методом заміни змінної.

На дошці записане рівняння. На цьому прикладі цього рівняння ми розглянемо спосіб розв’язання біквадратного рівняння.

х⁴ – 2х² - 8 = 0,

          (х²)² – 2х² - 8 = 0,

Нехай  х²=t, тоді

t²-2t-8=0; (розв’язати рівняння учень до дошки)

D=(-2)²-4·1·(-8)=4+32=36; D > 0,

                 t_1,2 =,     t₁=4,      t₂ =-2               

Обернена підстановка:

                 х²= 4;                       х²=-2;

                х = ±√4                     Ø

                 х₁ = - 2, х₂ = 2,        

Відповідь: х_1,2=± 2. (повторити схему розв’язання)

Зверніть увагу на екран. На ньому ще один приклад біквадратного рівняння. Давайте його розглянемо.

Приклад  №2 (на екрані, пояснення)

х⁴ – 5х² + 4 = 0,

          (х²)² – 5х² + 4 = 0,

Нехай  х²=t, тоді

t²-5t+4=0;

D=(-5)²-4·1·4=25-16=9; D > 0,

                                         

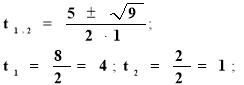
Обернена підстановка:

                 х²= 4;                       х²=1;

                х = ±√4                     х = ±√1

                 х₁ = - 2, х₂ = 2,         х₃ = -1, х₄ = 1

Відповідь: х_1,2=± 2 ,  х_3,4=±1.

А як видумаєте, скільки коренів може мати біквадратне рівняння? Давайте дослідимо це питання.

Учні кожного ряду отримують по одному рівнянню, розв’язують його.

х⁴-10х²+9=0, 2х⁴ –х²-1=0, х⁴+8х²+16=0

Потім ми зробимо висновок, скільки коренів можуть мати  біквадратні рівняння.

1 ряд  х⁴-10х²+9=0   4 кореня

 

2 ряд 2х⁴ –х²-1=0     2 кореня

 

 

3 ряд  х⁴+8х²+16=0  Немає коренів, бо D=0, але корінь від’ємний

 

 

Таким чином, біквадратне рівняння може мати 4, 2 корені або зовсім не мати коренів.

Давайте узагальнимо розглянуті приклади і складемо алгоритм розв’язання біквадратного рівняння:

1. Позначимо
2. Отримаємо аt² +вt+с=0
3. Розв’яжемо отримане рівняння, знайдемо t₁ та t₂
4. Виконаємо зворотну підстановку

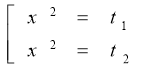
5. Якщо,                               коренів немає

Якщо , х=0

Якщо , 2 корені

6. Робимо висновок про кількість коренів біквадратного рівняння.
7. Записуємо відповідь.

 

V.  Домашнє завдання.

 І, нарешті, ви прибули на останню станцію «Домашня». Отже, отримайте своє домашнє завдання.

Опрацювати: стор. 260, вивчити алгоритм розв’язання біквадратних рівнянь; дослідити, чи може біквадратне рівняння мати 1 або 3 кореня; розв’язати: № 37.4.

VІ. Підсумок уроку.

 Наша подорож завершена. Що ви нового дізналися під час подорожі?

З яким новим поняттям ознайомились?