Урок. "Розв’язування вправ на знаходження n-го члена арифметичної прогресії та суми n перших її членів"
Розв’язування вправ на знаходження
n-го члена арифметичної прогресії
та суми n перших її членів
Вчитель математики
Кальницька З. Б.
Тема. Розв’язування вправ на знаходження n-го члена арифметичної прогресії та суми n перших її членів.
Мета: формувати вміння застосовувати властивість арифметичної прогресії до розв’язування вправ.
Тип уроку: комбінований.
Обладнання: Роздатковий матеріал, листи самооцінювання, ноутбук та мультимедійний проектор, завдання для самостійної роботи.
Хід уроку.
І. Організаційна частина. Повідомлення теми уроку. Постановка цілей і завдань.
Чого ви очікуєте від уроку? (Заслуховуються відповіді учнів)
Вступне слово вчителя. «Прогресія – це рух вперед».
Перша умова, якої треба дотримуватися в математиці, – це бути точним.
Друга – бути чітким,
І наскільки можливо, простим.
Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: «Арифметична прогресія», закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах історичних задач, будемо удосконалювати вміння оцінювати свої досягнення.
А результати своїх досягнень ми будемо заносити до листка самооцінювання.
Впишіть своє прізвище та ім’я.
Як виставляти бали і за які види робіт, то у нас існує технологічна картка, де описано кожен крок нашої роботи
Я очікую злагодженої роботи, взаємодопомоги, взаємоповаги, гарних результатів.
ІІ. Актуалізація опорних знань учнів(5хв).
- На дошці прикріплені аркуші, на зворотному боці яких записано питання. Учень навмання знімає аркуш, читає запитання та відповідає на нього. Якщо відповідь правильна, то аркуш перевертається на другу сторону, з якої написані букви і учень виставляє в свій лист само оцінювання бал. Якщо відповіді немає – відповідає інший учень з місця, за бажанням. Коли всі питання відкрито, на дошці можна прочитати прізвища видатних учених.
АБЕЛЬ, ГАУСС, ФУР’Є
Відповівши на запитання, ми прочитали імена математиків, що зробили внесок у розвиток вчення про послідовності, як ще говорять числові ряди. Деякі послідовності, властивості яких вивчали математики, названо їх іменами:
Гаусс Карл Фрідріх 1777 – 1855, Німеччина
Абель Нільс Хенрик 1802 – 1829, Норвегія
Фур’є Жан Батист Жозеф 1768 – 1830, Франція
Довідк. (доповідають учні, домашнє завдання)
Карл Гаусс, наприклад, коли ще навчався в школі, обчислював суму перших ста натуральних чисел:
Абель вивчав умови, за яких степеневий ряд збігається, тобто послідовність його сум має границю.
Фур’є ж розглядав, як різноманітні функції можна подати за допомогою тригонометричних рядів, і зробив ці ряди справжнім знаряддям математичної фізики.
Аркуші із запитаннями
|
Що таке d? |
Формула суми n членів |
Коли прогресія є зростаючою? |
Назвіть властивість арифметичної прогресії? |
Назвіть різницю арифметичної прогресії 4,3,2,1,0 |
|
Який член послідовності слідує за аn+4? |
Формула суми n членів |
Коли прогресія спадна? |
Що в арифметичній прогресії позначають буквою n? |
Чи є послідовність -3,-1,1,4,6 арифметичною прогресією? |
|
Яка послідовність називається арифметичною прогресією? |
Що записано? an+1 = a n + d.
|
Назвіть формулу для знаходження будь-якого члена арифметичної прогресії? |
Як знайти d? |
Різниця арифметичної прогресії дорівнює 2. Знайдіть її перший член, якщо а2=5. |
2. Робота з карткою формул.
Кожному учневі пропонують картку для перевірки знання формул. Учні вписують на картці своє прізвище та серед запропонованих формул вибирають правильні, які обводять кружечком.
Картка формул І Картка формул ІІ
1. ![]() 1. d = an+1 + a n
1. d = an+1 + a n
2. ![]() 2.
2. ![]()
3. ![]() 3.
3. 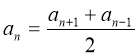
4. 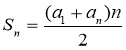 4.
4. ![]()
5. 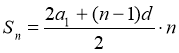 5.
5. ![]()
6. d = an+1 - a n. 6. ![]()
7. ![]() 7. d = an+1 - a n.
7. d = an+1 - a n.
8. ![]() 8.
8. 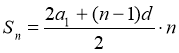
9. ![]() 9.
9. 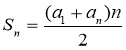
10. 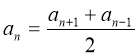 10.
10. ![]()
11. ![]() 11.
11. ![]()
12. d = an+1 + a n 12. ![]()
Правильні формули: 1, 4, 5, 6, 8, 10. Правильні формули 3, 5, 7, 8, 9, 12
Після виконання роботи аркуші здають учителю. Бали виставляють за кількістю правильних відповідей (кожна правильна відповідь — 1 бал).
ІІІ. Формування вмінь і навичок застосовувати властивість арифметичної прогресії та формулу n – го члена арифметичної прогресії.(20 хв)
Розв’язування вправ на дошці та в зошитах учнів під керівництвом учителя
Клас поділимо на дві групи.
Завдання класу
1 група.
- Арифметична прогресія задана двома першими членами: 1,3; 2,5;…Знайти наступні два члени. (3,9; 4,1)
- В арифметичній прогресії α1 = 2,3; d= -0,35. Знайти α29. (-7,5)
- Чому дорівнює сума перших семи членів арифметичної прогресії (αn), якщо α1 = 8 і α7 = 14? (77)
- Знайдіть суму перших десяти членів арифметичної прогресії (αn), якщо:
α3 = -40, α5 = 20. (350)
2 група.
- Арифметична прогресія задана двома першими членами: 4,9; 3,5;…Знайти наступні два члени. (2,1; 0,7)
- В арифметичній прогресії α1 = -8,6; d= 0,12. Знайти α26. (-5,6)
- Чому дорівнює сума перших шести членів арифметичної прогресії (αn), якщо α1 = 20 і α6 = 15? (105)
- Знайдіть суму перших десяти членів арифметичної прогресії (αn), якщо:
α2 = 70, α4 = -10. (-700)
ІV. Контроль і корекція знань учнів
Самостійна робота із взаємоперевіркою.
1 варіант.
- Знайдіть різницю арифметичної прогресії: 9; 6; 3; 0; -3.
А) 9; Б) 6; В) -3; Г) 3.
- Знайдіть суму перших чотирьох членів арифметичної прогресії (αn), якщо:
α1=3, d=7.
А) 54; Б) 30; В) 42; Г) 63.
- Дано арифметичну прогресію (αn). Знайдіть: α4, якщо а3=18, а5=22.
А) 1; Б) 40; В) 20; Г) 23.
- Знайдіть перший член арифметичної прогресії (αn), якщо: а2=81, а3=72.
А) 9; Б) 63; В) 90; Г) 56.
- За першу секунду тіло пройшло 20 м, а за кожну наступну проходило на 5 м більше, ніж за попередню. Знайдіть шлях, пройдений тілом за 8 с.
2 варіант.
- Знайдіть різницю арифметичної прогресії: 9; 12; 15; 18.
А) 9; Б) 6; В) -3; Г) 3.
- Знайдіть суму перших чотирьох членів арифметичної прогресії (αn), якщо:
α1=-3, d=7.
А) 54; Б) 30; В) 42; Г) 63.
- Дано арифметичну прогресію (αn). Знайдіть: α5, якщо а4=20, а6=26.
А) 1; Б) 40; В) 20; Г) 23.
- Знайдіть перший член арифметичної прогресії (αn), якщо: а2=65, а3=74.
А) 9; Б) 63; В) 90; Г) 56.
- Першого дня турист пройшов 5к м, а кожного наступного дня він проходив на 1км більше, ніж попереднього. Скільки кілометрів турист пройшов за 6 днів?
Відповіді
1 варіант В, А, В, В, 300.
2 варіант Г, Б, Г, Г, 45
Додаткове завдання номер з книжки, № 913 (а, б)
IV. Підбиття підсумків уроку. Рефлексія.
Підіб’ємо підсумок уроку. Чи досягли ми очікуваних результатів? (Учні підсумовують свою роботу, висловлюють думки щодо здійснення своїх очікувань)
Листи самооцінювання здаються вчителеві, який підбиває підсумки уроку,оголошує оцінки.
VII. Домашнє завдання
§21, впр.878, 882(а), 897(а)


про публікацію авторської розробки
Додати розробку
