Урок "Розв’язування вправ. Самостійна робота з теми "Функції,їх властивості і графіки""

Тема: Розв’язування вправ. Самостійна робота

Мета: удосконалити знання з теми «Функції, їх властивості та графіки, закріпити навички розв’язування вправ; розвивати логічне мислення; виховувати зацікавленість до вивчення даної теми

Тип заняття: практичне заняття.

Обладнання: підручники, презентація «Все про функції», картки для самостійної роботи.

Література:

1. Алгебра і початки  аналізу: підруч. для 10 кл. загальноосвіт. навч. закладів М.І. Шкіль, З.І. Слєпканеь, О.С. Дубинчук.-К.: Зодіак – ЕКО, 2007. – 272 с.

2. Математика: Підручник О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов,  А.К.Сліпченко – К.: Вища школа, 2001.-447 с.

3. Чекова А.М. Алгебра. 7-12 класи: Навчальний посібник – 5-те видавництво.-Х.: Країна лерій. 2007.-120 с.

План заняття

І. Організація початку заняття.

ІІ. Актуалізація опорних знань:

1. Продовжити речення
2. Дати відповідь на запитання
3. Знайти границі функцій
4. Знайти область визначення функцій
5. Знайти область значень  функцій

ІІІ. Самостійна робота

IV. Підведення підсумків заняття.

V. Домашнє завдання

Хід заняття

І. Організаційний момент

Рахунок і обчислення – основа порядку в голові.

                                                              Песталоцці

Знати математику – це насамперед уміти користуватися нею. Учитися користуватися математичними значеннями найкраще під час розв’язування задач.

ІІ. Актуалізація опорних знань:

1. Продовжити речення

• Відповідністю називають функцію, якщо…(кожному значенню змінної Х з деякої множини D відповідає єдине значення змінної У)
• Х називають …. (аргументом)
• У називають (функцією)
• Значення яких може набувати аргумент – це …(область визначення функції)
• Значення яких може набувати функція – це …(область значень функції)
• Парною називається функція, якщо …
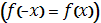
• Функція непарна, якщо …
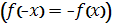
• Значення аргументу при яких значення функції дорівнює 0 – це … (нулі функції)

2. Дати відповідь на запитання

• Яка функція називається зростаючою?
• Яка функція називається спадною?

Приклад. Знайти проміжки та функції . Розв’язання: функція спадає при зростає при

• Що таке проміжки знакосталості?

Проміжки знакосталості – це проміжки з області визначення функції, на яких функція набиває додатних або від’ємних значень.

Щоб знайти ці проміжки треба розв’язати нерівність:

– додатні значення

– від’ємні значення

Приклад. Знайти проміжки знакосталості функції . Розв’язування: Оскільки - невід’ємне число при , то , при .

Від’ємних значень дана функція не набуває.

• Назвіть основні способи задати функції? (за допомогою формули, словесно, таблицею, аналітично, графічно)
• Дайте визначення «графік функції» -

Графіком функції називається множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати -  відповідним значеннями функції.

• Що таке нулі функції ?

Нулями функції називаються значення аргументу, при яких функція дорівнює нулю. Щоб знайти нулі функції треба розв’язати рівняння .

Приклад. Знайти нулі функції .

Розв’язання: ; 

Відповідь:

3. Знайти границі функцій

1. .

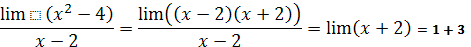Відповідь: 3

Відповідь: 1

4. Знайти область визначення функцій

1. 
2. 
3. ;   
4. ;

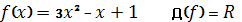
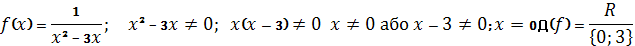
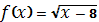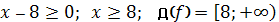
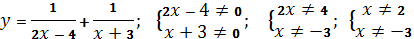Відповідь: Д(у)=

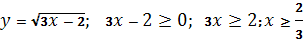5. Відповідь: Д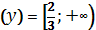

5. Знайти область значень функцій

А)               Б)        

Відповідь:            Відповідь:  

   В) ;    Відповідь: .

ІІІ. Самостійна робота

1 варіант                                                     2 варіант

1. Знайти область визначення функції (4 бали)

2. Знайти границі функції (2 бали)

3. Дослідити функцію на парність (непарність) ( 3 бали )

-парна     – не парна

не парна– парна

Розв'язання

1. Знайти область визначення функції (4 бали)

Відповідь: ДД

Д= або

Відповідь: Д                          Д

2. Знайти границі функції (2 бали)

=Відповідь:7

=Відповідь:

3. Дослідити функцію на парність (непарність) ( 3 бали )

- функція парна

-непарна

-непарна

- функція парна

IV. Підведення підсумків

V. Домашнє завдання

1. Дослідити функцію на парність (непарність)

1) – функція є ні парною, ні непарною 

–функція парна

2. Для функцій, графіки яких зображені на рис.1, а-г. Знайдіть:

1) точки мах і мін функцій;

2) екстремуми функцій