Навчально – методична карта заняття

Предмет : математика

Тема заняття: границя функції

Тривалість заняття: 2 год

Тип заняття: комбінований

Група: І курс, «Лікувальна справа», «Сестринська справа»

І. Актуальність теми:

 Границя функції важлива тема в курсі занять математики. Студент опановує знання з даної теми задля вдосконалення вмінь в обрахунках складних функцій.

ІІ. Навчальні цілі заняття:

 Студент повинен:

 Знати:

• Поняття границі в точці
• Особливості розв’язання основних границь

    Вміти:

• Застосовувати знання для розвязку границь

ІІІ. Цілі розвитку особистості (виховні):

• Виховання в учнів культури математичної мови;
• Виховання бажання працювати в групі;
• Розвивати самооцінку
• Прививати інтерес до вивчення математики.

ІV. Міждисциплінарна  інтеграція:

 Забезпечуючі дисципліни:

Інформатика, фізика.

V.Зміст теми заняття

Зміст теми заняття:

VІ.Зміст заняття

Сприймання поняття границі функції.

Побудуємо графік функції f(x) = х + 1 (рис. 9). Якщо х наближається до 1, то зна­чення у наближається до 2.

Говорять, що границя функції f(x) при х, що наближається до 1, дорівнює 2 і запи­сується: (x +1) = 2.

Розглянемо другий приклад.

Побудуємо графік функції g(x) = 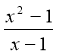і розглянемо  поведінку цієї функції при х, близьких до 1.

Функція g(x) = 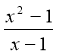визначена при х (-; 1) (1; +) і графік являє собою пряму у = х + 1 з виколотою точкою х = 1 (рис. 10),  бо функція g(x) =

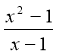=   не визначена в точці х = 1.

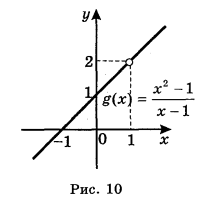Якщо х наближається до 1 (зліва чи справа), то у наближається до 2 (відпов­ідно знизу чи зверху).

 Отже, 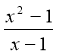=2.

Розглянемо третій приклад. Побудуємо графік функції

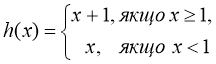(рис. 11) і розглянемо поведінку функції при х, що наближається до 1.

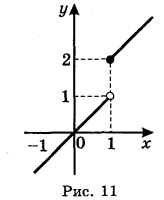При х → 1 (що наближається до 1) границі функції h(x) не існує, поскільки не існує єди­ного числа, до якого наближається функція при х, що прямує до 1.

(Якщо х наближається до 1 зліва, то h(x) наближається до 1; якщо ж х наближається до 1 справа, то h(x) наближаєть­ся до 2).

Таким чином:

Якщо при значеннях х, що прямують до дея­кого числа а, значення функції f(x) прямують до єдиного значення b, то говорять, що при х, що наближається до а, функція f(x) має границю, яка дорівнює b, і це записується так: f(x) = b або f(x) → b при х → а.

Виконання вправ

1. Використовуючи графіки функцій (рис. 12), з'ясуйте:

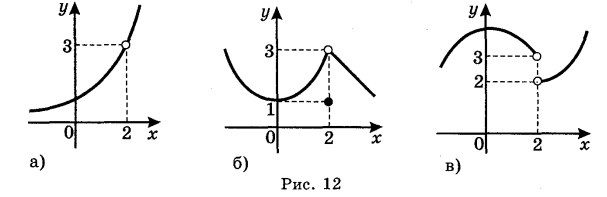
1) Чи має границю функція в точці х, що прямує до 2? Якщо має, то чому дорівнює ця границя?

2) Чи залежить існування границі функції в точці від визначе­ності функції в цій точці?

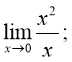3) Якщо функція визначена в точці, то чи завжди границя функ­ції дорівнює значенню функції в цій точці? 2. Користуючись графіком, знайти границі (якщо вони існують): a) б) в) г)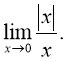

III. Осмислення поняття границі функції.

Нехай задано деяку функцію, наприклад, f(x) = 2х + 1. Розглянемо таблицю значень цієї функції в точках, що досить близько розташовані до числа 1 (і в самій точці 1), та знайдемо |х – 1| та |f(x) – 3| у відповідних точках.

З таблиці видно, що при наближенні значення аргументу до чис­ла 1 значення функції наближається до числа 3, при цьому по­хибка значень функції може бути досягнена як завгодно малою, шляхом зменшення похибки аргументу. Дійсно, взявши довільне ε > 0, тоді |f(x) – 3| < ε,

або |2х + 1 – 3| < ε; |2х – 2| < ε, 2|х – 1| < ε; |х – 1| < .

Отже, щоб похибка значень функції не перевищувала ε > 0, слід  взяти значення х такі, що |х – 1| < .

Число b називається границею функції у = f(x) в точці а, якщо для будь-якого ε > 0 існує таке число δ = δ(ε) > 0, що для всіх х: 0 < |х – а| < δ, виконується нерівність |f(x) – b| < ε. (Рис. 13).

Розглянемо приклад.

Доведіть, що (2x – 1) = 5.

Розв'язання Задамо довільне ε > 0 і покажемо, що існує δ > 0 таке, що із нерівності |х - 3| < δ випливає нерівність |(2х - 1) - 5| < ε. Маємо |(2х - 1) - 5| < є,

|2х - б| < ε;  |2(х - 3)| < ε;  2·|х - 3| < ε; |х - 3| < Отже, якщо взяти δ = , то виконання нерівності

| x - 3| < δ приведе до виконання нерівності |(2x - 1) - 5| < ε. Отже, згідно з означенням границі маємо: (2x -1) = 5.

Виконання вправи № 12 (3).

VІІ. ЛІТЕРАТУРА

1.               Алгебра і початки аналізу. Підруч. для 10–11 кл. серед, шк. / А. М. Колмогоров, О. М. Абрамов, ІО. П. Дудніцин та ін.; За ред. А. М. Колмогорова. – К.: Освіта, 1992. - 350 с.
2.                Бевз Г. П. Методика розв'язування алгебраїчних задач. - К.: Рад. шк., 1975. - 240 с
3.               Бевз Г. II., Бевз В. Г., Владимирова II. Г. Геометрія: Проб, підруч. для 10 - 11 кл. загальноосвітніх навч. закл. - К.: Вежа, 2002. - 223 с.