Урок "Розв'язування задач"
Про матеріал
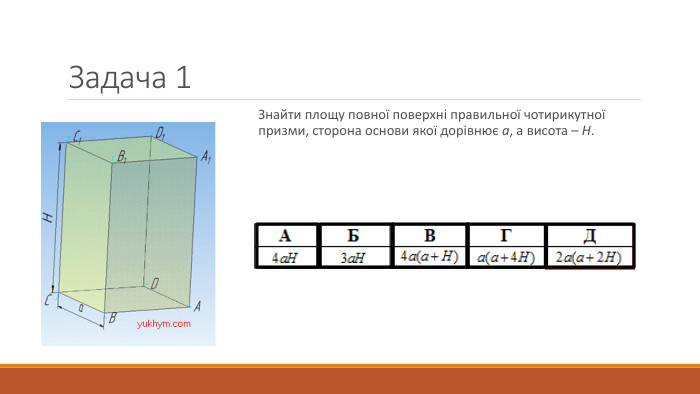
Матеріал може бути використаний при підготовці до ЗНО та на уроці геометрії при вивченні теми "Площа поверхні призми" Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку