Урок "Розв'язування задач з теми : Вектори у просторі"

Тема уроку: Розв’язування задач

Мета уроку:

 Навчальна: узагальнити та систематизувати знання і вміння учнів з теми «Вектори у просторі»; перевірити рівень засвоєння знань учнів з теми, вміння користуватися вивченим матеріалом.

Розвиваюча: розвивати пам’ять, вміння виділяти головне, швидко орієнтуватися в різних ситуаціях.

Виховна: виховувати інтерес до предмету, наполегливість у досягненні мети, дисциплінованість, вміння раціонально використовувати час уроку.

Тип уроку: узагальнення та систематизація вивченого матеріалу.

Хід уроку

І Організаційний етап

Учні заходять в клас і витягають колір своєї групи і сідають за парти які відмічені тими кольорами (так учні об’єднуються в групи)

Вчитель:

Доброго ранку! Сьогодні гарна погода, і настрій у вас, бачу, теж гарний.

Сьогодні у нас незвичайний урок, тому що присутні учні 9 і 10 класу.

 Американський винахідник Генрі Форд сказав:

    Зібратися разом - це початок,

    Триматися разом - це прогрес,

    Працювати разом - це успіх!

    Ми зібралися,тримаємося разом і починаємо працювати. Бажаю успіху! 

ІІ Актуалізація опорних знань

На столі у вчителя геометричні просторові  фігури і фігури, які розглядали на площині

Піраміда, циліндр, конус, призма, паралелограм, квадрат, трикутник, трапеція

• Що це за фігури?
• Де розглядали ми ці фігури?
• Піраміда, призма, конус це   (просторові фігури)
• Паралелограм, квадрат, трикутник, трапеція – це фігури які розглядали ми їх на площині.
• Чи можна розглянути  призму у площині?
• Що можна розглянути і в площині і в просторі? (вектор)
• Скільки координат має вектор?(учні 9 класу – два, 10 клас – три)
• Робимо висновок: якщо розглядати вектор у площині то він має дві координати, а якщо у просторі то він має три координати

Усне опитування

На дошці викладене число П з різнокольорових кружечків,  на яких записані початок речення , а кінець вони мають продовжити . До дошки виходить один представник групи, який зачитує запитання, а група має відповісти. Якщо група не може справитись з цим завданням то допомагають інші учні. В цей час учитель демонструє презентацію з теорією.

Наприклад:

Правильні відповіді висвітлюються на слайді (порівнюємо теоретичні відомомсті учнів про вектор у планіметрії та стереометрії)

Давайте з вами попрацюємо над завданнями. Вашій увазі завдання до вправи «Знайди помилку»

Вчитель:Учень, який готувався до ЗНО виконав завдання, нам потрібно перевірити чи правильно він їх виконав. Учні усно пояснюють хід виконання завдання

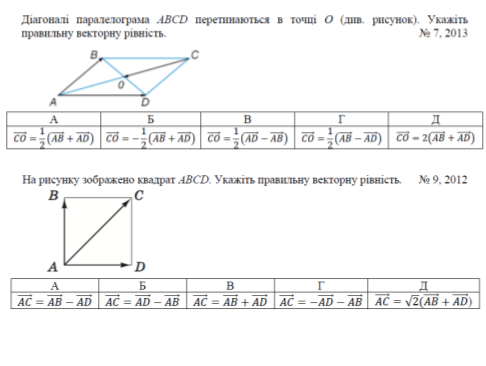
ІІІ. Мотивація навчання

Кожній групі в конверті задані картинки серед яких вони вибирають ті, в яких на їх думку можна говорити про вектор.

(картинки які вибирають учні прикріплюють на дошці)

Вчитель:На основі поданої інформації можна сказати, що поняття «вектор» широко використовується у всіх галузях нашого життя. І складно уявити собі життя без геометрії, як і геометрію без векторів.

IV.Розв’язування задач

(колективно)

2.Робота в групі

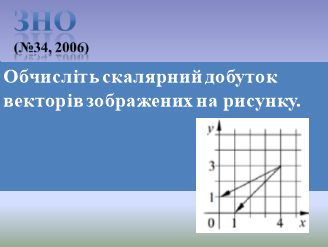
Завдання групи отримують на ватмані де і роблять записи.

3.Тестові завдання Quizziz

V. Підсумок уроку

1. Що ми робили?

Сьогодні на уроці ми повторювали додавання та віднімання векторів; властивості перпендикулярності і колінеарності векторів; скалярний добуток векторів і знаходження косинуса кута.

2. З якою метою?

Ми готувалися до контрольної роботи. А також розглянули особливості вишиванки кожної області України.

3. Які результати нашої діяльності?

Результат діяльності - це знання та практичні навички, які ви отримали протягом вивчення теми.

4. Як ми цього досягли?

Вивчали, повторювали матеріал, закріплювали його вправами.

5. Чи можна було зробити це краще?

Можна, якщо завжди прагнути до кращого. У нашому випадку добре вчитися. І все буде добре.

Вчитель:Вектор можна знайти і у житті, але для цього потрібно розрахувати свої сили,розвивати свої здібності Поставити пред собою мету і наполегливо до неї йти.

А мета увас і у нас одна  Успішно скласти ЗНО.

VІ. Домашнє завдання.

Учні отримують дидактичний матеріал.