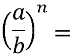Урок "Степінь з цілим від’ємним показником"

Тема    Степінь з цілим від’ємним показником

Мета.

Формування компетентностей:

предметної: засвоїти поняття степеня з цілим від'ємним показником та формувати вміння застосовувати його при розв'язуванні вправ;

ключові – інформаційно-цифрової; соціальної і громадянської; спілкування державною мовою, уміння вчитися впродовж життя.

Тип уроку:  засвоєння нових знань

 Обладнання: ноутбук, презентація,

Епіграф: "Нехай хто-небудь спробує викреслити з математики степені,

і він побачить, що без них далеко не поїдеш".

 М.В.Ломоносов

Хід уроку

І. Організаційний момент.

     1) Привітання

      2) Перевірка присутніх

ІІ. Тема

В робочих зошитах               число

                                          Класна робота

 Тема уроку:                  Степінь з цілим від’ємним показником

Мета:

Епіграф уроку:

ІІІ. Домашнє завдання , актуалізація опорних знань

     Учитель. На уроках алгебри в 7 класі ви вже відкрили для себе дивовижний світ степенів з натуральним показником. Багато учених у всі часи займалися питаннями їх вивчення. Це і знаменитий Піфагор, і Декарт(який, до речі, першим ввів позначення степеня).

 Пригадаємо все, що вивчили по темі: «Степінь з натуральним показником» в попередніх класах.

1)Вправа Продовжити речення

1. Степенем числа а з натуральним показником n, більшим за 1, називається добуток n множників, кожен з яких рівний а

2. Число а, яке підносимо до степеня, називають основою
3. Число n, яке показує до якого степеня підноситься основа називають показником
4. При піднесенні до степеня додатнього числа отримуємо додатнє число
5. При піднесенні до степеня від’ємного числа з парним показником отримуємо додатнє число
6. При піднесенні до степеня від’ємного числа з непарним показником отримуємо від’ємне число

2)Вправа Знайди пару (1б)

3) Обчислити (1б)

          1)

        2) =

    3) =

     4) =

ІІІ. Мотивація навчальної діяльності.

Учитель.

Рішення практичних завдань і оперування дій зі степенями викликало необхідність в узагальненні поняття степеня.

Доцільність введення нульового і відємного показників степеня і сучасних символів уперше детально описав в 1665г. англійський математик Джон Валліс. Його справу завершив Ісаак Ньютон, який почав систематично застосовувати нові символи, після чого вони увійшли до загального ужитку.

(Учитель демонструє портрети учених школярам)

Джон Валліс    Ісаак Ньютон

Отже,

 ІV.  Нова тема  

 Продовжити числові ряди (один із яких складається із значень сте­пенів деякого числа, а другий — із самих відповідних степенів):

        1 ряд: 1000,  100,   10,        1,        ,     ,     ,        …

        2 ряд: 10³,      10²,   10¹,                 …

                                                       П Р О Б Л Е М А

 Порівнюємо

1ряд:  кожне число менше від попереднього в 10 разів. 

2ряд:  показник степеня починаючи з другого на 1 менший від показника попереднього степеня на 1).

Узагальнюємо  Розв’язання проблеми. ( Якщо поширити цю закономірність на числа, що стоять праворуч від 10¹  отримаємо:

10³, 10², 10¹, 10⁰, 10^-1, 10^-2, 10^-3. )

Отже   10⁰ =1,             10^-1 = ,      10^-2 = ,        10^-3 = .     

 (Мікропідсумок)Тобто числа  можна записати у вигляді степеня з від’ємним показником.

Питання.    Чи можемо ми взяти степінь з іншою основою?

Відповідь      Так   Окрім 0.

Конспект

V. Формування вмінь і знань    Учитель. Відомий математик Рене Декарт відмічав, що недостатньо мати хороший розум, головне - його раціонально застосовувати.

VІІ. Застосування знань - формування умінь і навичок.

 Учитель.Успіх - це результат певних умінь і навичок. Тому, щоб досягти успіху формуватимемо уміння і навички в процесі розв’язування прикладів

Робота з підручником….

VІІІ,  Тести

ІX. Підведення підсумків.

Де ви можете застосувати знання отримані сьогодні на уроці?

Степінь навколо нас Слайди

Завершальне слово учителя.

Сьогодні ви ще раз переконалися, що світ степенів дивовижний. Правий був Ломоносов, сказавши, що без них далеко не поїдеш.

X. Домашнє завдання.

За підручником  А.Г.Мерзляк, В.Б.Полонський, М.С.Якір для 8 класу: Алгебра для загальноосвітніх навчальних закладів:– Х.: Гімназія, 2016

1.Опрацювати п. 8    № 233, 235, 240, 243

2. Відшукати історичні відомості про степінь з цілим від’ємним показником

Дякую всім за роботу, молодці!