Тема. Квадратні рівняння. Зведене квадратне рівняння. Теорема Вієта.

Тема. Квадратні рівняння. Зведене квадратне  рівняння. Теорема  Вієта.

Мета: перевірити вміння учнів розв’язувати рівняння, вести поняття зведеного квадратного рівняння; довести теорему Вієта; ознайомити учнів з  їх застосуванням та історичною довідкою; розвивати логічне мислення, вміння аналізувати, порівнювати, робити  висновки.

Хід уроку

І. Організаційний момент.

ІІ. Перевірка виконання домашнього завдання.

Якість виконання домашнього завдання перевіряється зібравши на при кінці уроку зошити.

ІІІ.  Актуалізація опорних знань.

• Яке рівняння називається квадратним?
• Які види квадратних рівнянь ви знаєте?
• Яке рівняння називається неповним?
• Скільки видів неповних рівнянь?
• Від чого залежить кількість коренів повного квадратного рівняння?
• Чому дорівнює дискримінант квадратного рівняння?
• Як залежить кількість коренів квадратного рівняння від дискримінанта?
• Формули коренів повного квадратного рівняння.

1.Два учні виконують індивідуальні завдання з подальшим поясненням.

1-й учень . Розв’язати рівняння  х²+2| х|-3 =0.

                                                                (х₁=-1; х₂ =1.)

2-й учень. Розв’язати рівняння   х²+3х-10=0.

                                                                   (х₁=-4;х₂=2)

2.Знайти помилку.

а) 5х² +3х -2 =0.

D =9+40=49   ;

  .

б) х² +6х +8 =0.

D =36-48 =4; ;

в) х²+7х -12 =0.

D =49-4·1·12=1;

 

ІV. Самостійна робота.

Кожен учень о отримує один з тестових варіантів завдань на картках.

  Відповіді учні записують у спеціальні таблиці.

Оцінювання: завдання 1-4 –по 2 бали, завдання 5 –по 4 бали. Завдання складено так, що у кожному варіанті до першого завдання правильна відповідь А, до другого –В, до третього –Б, до четвертого –А, до п’ятого –Б. Тому вчитель відразу на уроці має можливість перевірити самостійну роботу за допомогою перфокарти і виставити оцінки, а учні –побачити свої помилки.

 Картка 1

1.3х²-11х -4 =0. А. -; 4. Б. ;-4. В. -1; 12.

      2. х² -3х +4 =0. А. 4; -1. Б.-4; 1. В. Немає коренів.

     3. х²-3х -4 =0   А. -1;1 . Б.-1; 4. В. 1;-2.

    4. х⁴ +х² -2 =0. А. -1;1. Б 1; -2. В.1;

   5. (х² +9) ²-14 (х² +9) +40 =0.   А.±1;±13. Б. .±1. В. ;±13

 

Картка 2.

1.3х²+4х-20=0. А. -3; Б. 3; -2. В. -10;6.

2.  х² -2х +3 =0. А. -1;3. Б. -3; 1. В. Немає коренів.

3.  х²+4х +4=0. А.2. Б.-2. В. Немає коренів.

4. х⁴+5х -6=0. А. .±1. Б. 1; -6. В. .±1; .±

       5.(х² -5)² +8(х² -5) +12 =0.    А. .±1;±7. Б. ±1. В. ±7

 

Картка3

1.3х²-4х -20 =0.   А. 3; -2. Б. -3; 2. В. -10; 6.

2. х²+3х+4 =0.     А. -4;1.     Б. 4; -1.   В. Немає коренів

3. х² +2х +1 =0.   А. 1.  Б. -1.  В. Немає коренів

4. 2х⁴+х² +1 =0.   А. .±1. Б. .±1; ±2. В. 1; -2.

5.(х² +4)² -7.(х² +4) +10 =0.     А. 5;2.    Б. .±1.  В. Немає коренів

Картка4

1. 3х²+11х -4 =0.     А. ; -4. Б. -; 4.     В. -1; 12

2. х² +2х +3 =0.       А. -3; Б. -1; 3. В. Немає коренів

3. х⁴ -4х +4 =0.        А. -2; Б. 2.     В. Немає коренів

4. х⁴ +4х² -5=0.       А.  .±1. Б. 1; -5.  В. .±1; ±.

5. (х² +3)² -9(х² +3) +14 =0.    А. 7;2. Б. ±2. В. Немає коренів

Таблиця відповідей

Прізвище
Відповідь Завдання	А	Б	В
1
2
3
4
5

 

V. Вивчення нового матеріалу.

На дошці рівняння:

1.х² -6х+5=0.

2. х² +5х+6=0.

3. х² -9х+20=0.

    Пояснення

Що спільного ви помітили в цих рівняннях? (Перший коефіцієнт дорівнює 1.)

  Квадратне рівняння називається зведеним, якщо перший його коефіцієнт дорівнює одиниці.

  Формулюємо теорему Вієта і доводимо її.

Якщо зведене квадратне рівняння має два корені, то їх сума дорівнює другому коефіцієнту рівняння, взятому з протилежним знаком, а добуток –вільному члену.

                                      Доведення

х² +рх +q =0-зведене квадратне рівняння, х₁ і х₂ –його корені, причому х₁≠ х_{2 .}Доведемо , що х₁+х₂= -р, х₁ ∙ х₂= q.

Розв’яжемо  дане рівняння за формулами коренів повного квадратного рівняння:

D = р²- 4 q;

Додамо та перемножимо корені рівняння й одержимо:

 

 

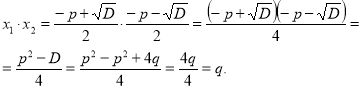
Теорему доведено.

 

VІ. Закріплення нового матеріалу.

 Учитель пропонує перевірити правильність теореми Вієта для рівнянь, зображених на дошці. Перший ряд розв’язує перше рівняння і перевіряє правильність теореми Вієта; другий – друге; третій –третє. Учні роблять висновки.

    Учитель. Для теореми Вієта існує обернена теорема.

    Якщо сума і добуток чисел m і n дорівнюють відповідно –р і q, то m і n – корені рівняння х² +рх +q =0.

Учні зачитують теорему з підручника .

Учитель. З теореми Віта випливає , що цілі розв’язки рівняння х² +рх +q =0 є дільниками числа q. Користуючись оберненою теоремою, можна перевірити , чи є певні числа коренями зведеного рівняння, чи ні. Це дає можливість усно розв’язувати зведені квадратні рівняння .

Розв’яжемо усно( завдання на дошці)

1.х² +7х +10=0.

2. х² -6х +8 = 0.

3. х² -10х +9 =0.

VІІ. Історична довідка – повідомлення учня.

Вієт Франсуа  (1540-1603) французький математик, народився в місті Фонтенте-ле-Конт. За професією юрист

  Здобувши юридичну освіту, спочатку був адвокатом, а згодом став радником  французького короля Генріха ІV. Незважаючи на велику службову завантаженість, Вієт з великим інтересом вивчав математику, присвячуючи цьому свій вільний час. праву Завдяки його роботам вона стала наукою про алгебраїчні рівняння, в основу якої покладено символічні позначення.

   Заслугою Вієта було те, що він першим почав позначати буквами не лише невідомі, а й дані величини, тобто коефіцієнти рівнянь. Це дало можливість записувати властивості рівнянь і їх коренів загальними формулами.

     Відомі величини та коефіцієнти Вієт позначав приголосними буквами b, c, d,…, а невідомі голосними a,o,e,…

   Вієту належать перші визначені успіхи в загальній  теорії алгебраїчних рівнянь, а саме: перетворення  рівнянь за допомогою різних підстановок, з’ясування залежності між коренями та коефіцієнтами, встановлення загального способу розв’язування рівнянь другого , третього і четвертого степенів тощо.

     У житті Вієта був цікавий факт. Під час війни Франції з Іспанією іспанці використовували для свого листування складний шифр, який французи ніяк не могли розгадати. Король Франції Генріх ІV звернувся до Вієта з пропозицію розшифрувати іспанські листи. Після наполегливої роботи йому вдалося це зробити. Протягом двох років французи перехоплювали і прочитували таємні листи до іспанського двору. Це давало великі переваги французькому командуванню. Армія Франції  завдала ряд поразок армії Іспанії. Іспанці зрозуміли причину своїх невдач і дізналися , хто розшифрував їхній тайнопис.

    Іспанські інквізитори, які відзначалися особливою жорстокістю, вважали, що людині не під силу розкрити таємницю їхнього шифру, і звинуватили Ф. Вієта в спілкуванні з нечистою силою. Ф.Вієта було засуджено до спалення. На щастя, Генріх ІV не видав його інквізиції.

 Роботи з математики Вієт писав надзвичайно важкою мовою і тому вони були не дуже популярними. Праці Вієта після його смерті зібрав професор математики в Лейдені Ф.Шоотен і видав у 1645р. під назвою «Opera Vital ».

   Ф.Вієт зробив великий внесок у розвиток математики та астрономії. Його називають батьком алгебри, а його іменем на видимій стороні Місяця названо кратер.

 

VІІІ. Підсумок уроку.

ІХ. Домашнє завдання. §42, виконати № 410,412,413