Урок "Сума перших n членів арифметичної прогресії" (9 клас)

Тема: Сума перших членів арифметичної прогресії. (9 клас)

Мета: навчати обчислювати суму перших членів арифметичної прогресії, записувати вивчені формули відповідно до умови задач та використовувати їх на практиці; підвищити інтерес до предмета, розвивати системність і послідовність мислення; виховувати розуміння ролі математики у житті, аргументовано відстоювати свої погляди.

Тип уроку: урок засвоєння нових знань, навичок і вмінь.  

Форма: індивідуальна, фронтально-колективна та групова.

Обладнання і наочність: підручник, дошка, зошити, комп’ютер\телефон, презентація, додаток «Kahoot».

Підручник: Мерзляк, Полонський, Якір, Алгебра 9 клас

Хід уроку

1. Організаційний момент. (2 хв.)
2. Актуалізація опорних знань. (10 хв.)

Гра в Kahoot. Повторення теми «Числова послідовність» і «Арифметична прогресія».

Молодці!

3. Формування нових знань. (20 хв.)

Тема сьогоднішнього урока звучить так «Сума перших членів арифметичної прогресії».

Нехай – сума перших членів арифметичної прогресії:

Відомо, що .

Тепер маємо

Якщо врахувати формулу (2) -го члена арифметичної прогресії, то

За формулами (1), (2) підраховують суму перших n членів арифметичної прогресії.

Сума перших членів арифметичної прогресії:

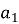1.           Якщо і 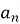— перший і 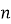-й члени арифметичної прогресії (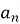), то сума 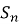перших 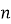членів цієї прогресії дорівнює за першою формулою.
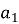2.           Якщо і 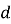— перший член і різниця арифметичної прогресії (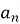), то сума 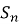перших 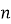її членів дорівнює за другою формулою.

Приклад. Відомо два члени арифметичної прогресії: Знайдіть

Розв’язання. Згідно з формулою n-го члена арифметичної прогресії

Отже, , звідки .

За формулою (1) знаходимо:

Відповідь:

Приклад. Знайти суму всіх тризначних чисел, які діляться на 7.

Розв’язання. Найменше тризначне число, яке ділиться на 7, дорівнює 105, а найбільше – 994. Всі тризначні числа, які діляться на 7, утворюють арифметичну прогресію 105, 112, 119, …, 994, у якої Згідно з формулою n-го члена

звідки . Тепер, використовуючи формулу (2), знаходимо:

Відповідь:

4. Застосування знань, вмінь і навичок. (45 хв.)

Завдання. Мерзляк 9 клас №17.1, №17.3, №17.5, №17.7, №17.9, №17.11, №17.12, №17.13, №17.15, №17.21, №17.23, №17.24, №17.28, №17.36

5. Підсумки урока. (2 хв.)

Ми з вами гарно попрацювали. Молодці!!!

• Мені стало зрозуміло.
• Я зрозумів, що зможу...
• У мене вийшло …

6. Домашнє завдання. (1 хв.)

Завдання. Підручник Мерзляк, Алгебра 9 клас №17.2, №17.4, №17.8, №17.10, №17.14, №17.16, №17.22