Урок геометрії, 10 клас

Теорема про три перпендикуляри.

Тип уроку: застосування знань, умінь, навиків

Хід уроку:

І. Організаційна частина.

а)Створення комфортного мікроклімату, привітання учнів

б)  Задачі за готовими малюнками:

на комп’ютерах 4 учні виконують завдання за готовими малюнками (додаток 1).

в) Клас розв’язує завдання за карткою теоретичного контролю знань(додаток 2).

ІІ. Актуалізація опорних знань

а) на дошці два учні розв’язують задачу:

№1. Сторона рівностороннього трикутник а дорівнює 3 см. Точка А віддалена від кожної вершини трикутника на 5 см. Обчислити відстань від точки А до площини трикутника.

№2 відстані від точки А до всіх сторін квадрата дорівнюють 5 см. Обчислити відстань від точки А до площини квадрата, якщо діагональ квадрата дорівнює 8см.

б) 3 учні дають відповідь на запитання ( вправа « Мікрофон»):

 

1. Які площини називаються  паралельними ? 
2. Скільки площин, паралельних даній можна провести через точку поза данною площиною ?
3. Якщо   дві   паралельні   площини перетинаються  третьою,  то  як розташовані прямі  перетину?
4. Які прямі у просторі називають перпендикулярними?
5. Як співвідносяться прямі, які перетинаються і відповідно паралельні перпендикулярним прямим?
6. Дайте означення перпендикулярності прямої і площини.
7. Назвати ознаку перпендикулярності прямої і площини.
8. Як розташована  площина, перпендикулярна до однієї з двох паралельних прямих, по відношенню до другої прямої?
9. Як розташовані  дві прямі, перпендикулярні до однієї і тієї самої площини?

      10. Що таке перпендикуляр, опущений з даної точки на площину?

      11. Що називається відстанню від точки до площини?

      13. Що таке проекція похилої?

Розв’язування задач відповідно рівню засвоєних знань.

а) низький рівень :№ 408 - № 410 ;

б)середній рівень : № 411 -№ 416;

в) достатній рівень: № 421 -№ 428;

г) високий рівень: № 434 -№ 437.

Пояснення та розбір на дошці задач, які викликали затруднення.

а)Повторити §§ 10; 11;

б) Розв’язати № 417; № 429; № 432.

 

 

Список використаної літератури

 

1. М.І. Бурда «Геометрія 10»:підручник для 10 класу загально-освітніх навчальних закладів: академічний рівень/ М.І. Бурда, Н.А. Тарасенкова  -К: Зодіак –ЕКО,2010. -176 с.
2. Погорелов О.В.   Геометрія : стереометрія, підручник для 10-11 класів середньої школи/ Погорелов О.В. - Київ, «Освіта», 2000р.-129.
3. Капіносов А.М. Геометрія 10 клас:дидактичні матеріали для різнорівневого навчання/ Капіносов А.М. – Дніпропетровськ, видавничо-поліграфічне підприємство «Дніпро»,1993р. -132.
4. О.М.Роганін тест- контроль «Алгебра і  початки аналізу + геометрія 10» / Роганін О.М. – Харків, «Весна», ФОП Співак Т.К.,2009р. -127с.

 

 

 

 

 

 

 

 

 

Додаток №1

Теорема про три перпендикуляри.

Задачі на побудову за готовими малюнками

Варіант 1

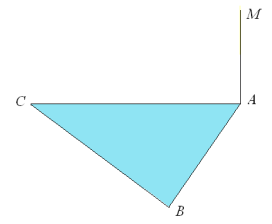
№ 1. Відрізок  МА – перпендикуляр до площини рівностороннього трикутника АВС. Провести через точку М перпендикуляр до прямої  СВ. Пояснити доцільність побудови.                           

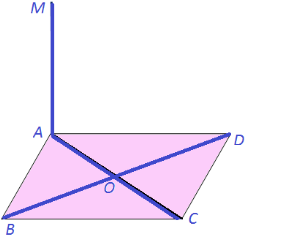
№ 2  О – точка перетину діагоналей квадрата ABCD . довжина якого відрізка є відстанню від точки М до діагоналі АВ? Відповідь обґрунтувати.

Теорема про три перпендикуляри.

Задачі на побудову за готовими малюнками

Варіант 2

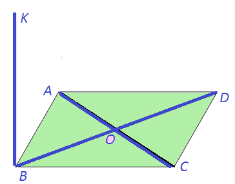
№1.  АВСD – квадрат, ВК(АВС).Довжина якого відрізка є відстанню від точки К до сторони  АD ?   Відповідь обґрунтувати.  

 

 

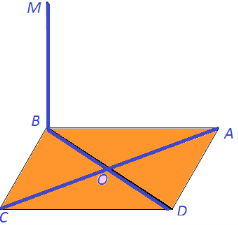№2. Відрізок  МВ – перпендикуляр до площини прямокутника ABCD . Провести через точку М перпендикуляр до прямої  AC. Пояснити доцільність побудови.

 

Теорема про три перпендикуляри.

Задачі на побудову за готовими малюнками

Варіант 3

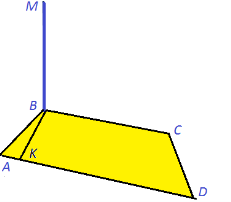
№1.  BK– висота трапеції ABCD,  BM(ABC). Довжина якого відрізка є відстанню від точки  M  до сторони AD? Відповідь обґрунтувати.                

 

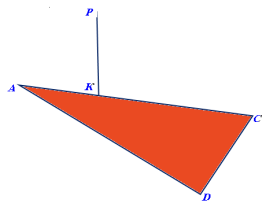
№2.  Відрізок РК– Перпендикуляр до площини прямокутного трикутника(С= 90⁰). Провести через точку Р  перпендикуляр до прямої DС.

Теорема про три перпендикуляри.

Задачі на побудову за готовими малюнками

Варіант 4

№1.Площини рівносторонніх трикутників ABC  і АСD взаємно перпендикулярні. К – медіана, ВК=2см. Обчислити відстань між точками В і D.

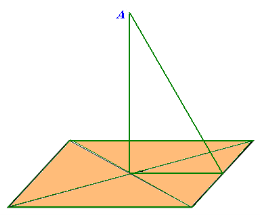
     №2.Відстань від точки А до всіх сторін квадрата дорівнює 5 см. Обчислити відстань від точки А до площини квадрата, якщо діагональ квадрата дорівнює см

 

 

 

 

 

 

 

Додаток 2

Теорема про три перпендикуляри

Картка теоретичного контролю знань

Варіант 1

Прізвище,ім.’я

1.Перпендикуляром , проведе-ним з даної точки до  даної площини називається

 

2.Якщо порівняти перпен-дикуляр і похилу, проведені з однієї точки, то довжина похилої

довжини перпендикуляра.

3. Відстанню від прямої до паралельної  їй площини називають

 

4. За відстань  між паралельними площинами приймають

 

 

5. Сформулюйте теорему, обернену до теореми про три перпендикуляри

 

 

6.Якщо точка  однаково віддалена від  усіх вершин многокутника, то основа перпендикуляра з неї є

 

7.Яка градусна міра кута між прямою і площиною, якщо пряма перпендикулярна до площини?

 

8. Вкажіть вид паралелограма, якщо точка рівновіддалена від усіх його сторін 

 

Варіант 2

Прізвище,ім.’я

1.Проекцією похилої нази-вають відрізок, який

 

2.Якщо з точки, взятої поза площиною, проведені дві рівні похилі, то їх проекції

 

3.Відстанню від точки до площини називають

      

4.Сформулюйте теорему про три перпендикуляри

 

 

 

5.Якщо точка  однаково відда-лена від  усіх сторін многокут-ника, то  основа перпенди-куляра з неї є                                                                                                                                                                         

6. Яка градусна міра кута між прямою і площиною, якщо пряма паралельна до площини?

 

7. Кутом між прямою і площи-ною називається кут

 

 

 

8. Вкажіть вид паралелограма, якщо точка рівновіддалена від усіх його вершин