Урок "Теорема про три перпендикуляри"

Тема. «Теорема про три перпендикуляри»

 

Мета: повторити поняття похилої, проекції похи­лої, кута між похилою та площиною; ознайомити учнів з формулюванням і доведенням теореми про три перпендикуляри; формувати навички використан­ня даної теореми до розв’язування задач; розвивати просторову уяву учнів, математичну мову, вміння обґрунтовувати власну думку; виховувати наполегливість, самостійність.

Тип уроку. урок засвоєння нових знань.

 

Хід уроку

І .Організаційний момент.

Перевірка готовності учнів до уроку, налаштування на роботу.

 

ІІ. Перевірка домашнього завдання.

Розв’язання задач перевіряється за малюнками, які викладач заздалегідь підготував на дошці. При розв’язанні задач звертаємо увагу на обґрунтування.

 

ІІІ. Актуалізація опорних знань.

1. Учні отримують аркуш із завданням продовжи­ти означення, вибравши його закінчення серед за­пропонованих відповідей.

Завдання	Варіанти відповідей
Перпендикуляром, опущеним з даної точки на дану площину, називається....	а) ... відрізок, що сполучає основи перпендикуля­ра і похилої, проведених з однієї і тієї самої точки.
Відстанню від точки до площини називається....	б) ... будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини.
Похилою, проведеною з даної точки до даної площини, називається....	в) ... кут між похилою і проекцією цієї похилої на площину.
Проекцією похилої називається ....	г) ... довжина перпендикуляра, опущеного з цієї точки на площину.
Відстанню від прямої до паралельної їй площи­ни називається....	д) ... відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини.
Кутом між похилою і площиною називається ....	е) ... відстань від будь-якої точки цієї прямої до площини.

 

Відповіді відразу перевіряються по коду на скритій дошці.

1.	2.	3.	4.	5.	6.
д	г	б	а	е	в

 

2. Двоє учнів біля дошки виконують завдання за готовими малюнками.

1. Назвати перпендикуляр, похилу та проекцію похилої, (мал.1)якщо АСВ = 90°.

2. Побудувати кут між площиною і похилою АВ

 

                 

 

Додаткові запитання

1.                    З даної точки проведені до площини дві різні за довжиною похилі. Що можна сказати про довжини проекцій цих похилих?

    2. Чи завжди дві рівні похилі мають рівні проекції?

         3. Чи має значення для знаходження кута між пло­щиною і похилою, з якої точки похилої проведено перпендикуляр до площини? Чому?

IV. Мотивація навчальної  діяльності учнів.

Задача 1. Через вершину прямого кута С трикут­ника АВС проведено перпендикуляр СD до його пло­щини. Побудувати найкоротшу відстань від точки D до гіпотенузи АВ.

Задача 2. Джерело світла знаходиться в центрі стелі кімнати, що має форму прямокутного паралелепіпе­да. Вказати точки на підлозі та на плінтусі (ребрі DС) підлоги, де освітлення буде максимальним.

 

             

 

 

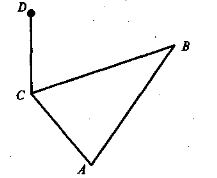
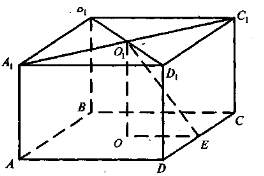
У першій задачі найкоротшою буде відстань DЕ (DЕАВ). Розв’язуючи другу задачу, слід вказати дві точки О і Е, де освітлення буде максимальним.

 

 

V. Повідомлення теми, мети і завдань уроку.

Один з найважливіших етапів розв’язування стереометричних задач – побудова та обґрунтування відстаней від точки до прямої і площини. В обох задачах необхідно обґрунтувати висунуті гіпотези про найкоротші відстані, тобто дослідити залежність між перпендикулярністю прямих і пло­щин у просторі.

Пропоную учням згадати, в яких випадках із жит­тя йдеться про найкоротшу відстань від точки до пло­щини.

VІ. Засвоєння нових знань.

Теорема: Якщо пряма, проведена на площині че­рез основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої.

Дано: АВ ; С; с; сВС.

Довести: сАС

Доведення:

(Доведення теореми проводимо разом з учнями класу у формі бесіди.)

Нехай АВ — перпендикуляр до площини , АС — похила і с — пряма у площині , що походить через основу С похилої.

Проведемо пряму СА₁, що паралельна прямій АВ. Вона буде перпендикулярною до площини . Через прямі АВ і СА₁ проведемо площину . Пряма с перпендикулярна до прямої СА₁, що належить площині . Тому пряма с перпендикулярна до площини , звідки випливає, що сВС, сАС.

 

 

Просимо учнів сформулювати твердження, яке є оберненим для доведеного, і довести його самостійно, аналогічно попередній теоремі.

Теорема: (обернена) Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна до проекції похилої.

VІІ. Формування вмінь і відпрацювання навичок.

Усні вправи

Задача 3. У задачі 2 знайти відстань від центра верх­ньої основи паралелепіпеда до ребра DС за умови, що АD = 8 м, АА₁ = 3 м.

Задача 4. У задачі 1 знайти, якою буде довжина перпендикуляра СD, якщо ЕD — 5 см і точка Е ділить гіпотенузу на відрізки довжиною 2 см і 8 см.

Задачі за готовими малюнками

№1. Дано куб АВСDА₁В₁С₁D_1. Назвіть і обґрунтуйте відстань:

а) від точки С₁ до прямої АВ;

б) від точки В до прямої D₁ А₁;

в) від точки  А₁ до прямої ВD.

№2. Відрізок МВ перпендикуляр до площини квадрата АВСD. Укажіть користуючись малюнком які з кутів прямі.

а) МВА;    б) МВD;    в) МDА;    г) МDС;    д) МСD.

№3. Відрізок НА – перпендикуляр до площин прямокутногоАВС(С=90°). Укажіть прямі кути.

а) НВА;    б) НАС;    в) СНА;    г) ВАН;    д) НСВ; е) НВС.

VIІІ. Самостійна робота.

Для засвоєння теореми про три перпендикуля­ри та формування навичок її використання до розв’язування задач учням пропонується навчальна са­мостійна робота. За потреби, викладач надає учням допомогу.

1-й варіант

1.                    У АВС  САВ = 30°, а АСВ = 60°. Відрізок АD перпендикулярний до площини  АВС. Довести, що DВ ВС.
2.                    Діагоналі квадрата АВСD перетинаються в точці О. Через точку О проведений перпендикуляр ОМ до площини квадрата. Знайти відстань від точки М до сторони СD якщо АD= 6 см, ОМ = 4 см.
3.                    Через точку О перетину діагоналей ромба АВСD проведений до його площини перпендикуляр ОМ. Довес­ти, що точка М рівновіддалена від усіх сторін ромба.

2-й варіант

1. У АВС  АВС = 90°, а відрізок АD перпенди­кулярний до площини  АВС. Довести, що DВВС.

2.  Через вершину С прямокутника АВСD проведе­ний перпендикуляр СК до площини цього прямокут­ника. Знайти відстань від точки К до сторони АD, якщо DС = 4 см, СК = 3 см.
3.  Діагоналі ромба дорівнюють 12 см і 16 см. Точ­ка М, яка не належить площині ромба, віддалена від усіх сторін ромба на 8 см. Знайти відстань від точки М до площини ромба.

IХ. Підсумок уроку.

- Сформулюйте теорему про три перпендикуляри.

- Які теореми й означення були використані в ході доведення теореми про три перпендикуляри?

Х. Домашнє завдання.

Опрацювати параграф. Довести обернену теорему.

Розв’язати задачі.

Середній рівень

№1. МА – перпендикуляр до площини прямокутногоАВС з гіпотенузою АВ. Доведіть, що МС ВС.

№2. АВСD – паралелограм, SВ(АВС). SСD - прямокутний(SСD=90°). Доведіть, що АВСD – прямокутник.

Достатній рівень

№3. Дано ромб АВСD, діагоналі якого перетинаються в точці О; СС₁ – перпендикуляр до площини ромба. Доведіть перпендикулярність прямої ВD і площини С₁ОС.

№4. До площини прямокутника АВСD проведено перпендикуляр FK. Побудуйте перпендикуляр, проведений із точки F до прямої АВ.