Тема.  Теорема Птолемея

Мета: довести теорему Птолемея; показати її застосування до розв’язуванні задач; розвивати кругозір; виховувати культуру математичного  мовлення; перевірити рівень засвоєння учнями знань.

Тип уроку: комбінований.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

ІІІ. Формулювання мети і завдань уроку

                                         …У величезному саду геометрії кожний може                                                                                                           

                                             підібрати собі букет за смаком.

                                                                                   Давід Гільберт                                                                         

Ми з вами починаємо вивчати дивовижні теореми. Одна із таких теорем – теорема давньогрецького вченого Клавдія Птолемея              ( ІІ ст. н. е.).

ІV. Сприйняття та усвідомлення нового матеріалу

Історична довідка

Птолемей Клавдій , давньогрецький вчений. Він розробив  так звану Геоцентричну систему світу. Біографічних відомостей про Птолемея дуже мало: відомо, що він провів велику частину життя в Александрії, де в 127-151р. проводив астрономічні спостереження. Основна робота Птолемея з астрономії  –  «Велика математична побудова астрономії в 13 книгах» –  «Альмагест».

Виключно велике було практичне значення цієї роботи для мореплавання і визначення географічних координат. А теорема знадобилася олександрійському астрономові Клавдію Птолемею, для складання таблиці синусів, точніше, таблиці довжин хорд, дуже потрібних для астрономічних розрахунків.

Теорема Птолемея. У всякому чотирикутнику, вписаному в коло, добуток діагоналей дорівнює сумі добутків його протилежних сторін.

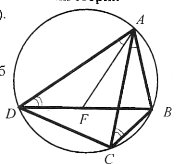                    Доведення.

Чотирикутник АВСD вписаний у коло. Доведемо, що АС · ВD = АD · ВС + DС · АВ.

АDВ = АСВ так як спираються на одну дугу. Проведемо відрізок АF ( точка F є ВD) так, щоб DАС = САВ. Тоді ∆АВС ~ ∆АFD за двома кутами. Звідси АD : АС = DF : ВС, тобто  АD · ВС =   АС · DF.

DСА = DВА так як спираються на одну дугу, а DАС = FАВ за властивістю вимірювання кутів. Тоді ∆DАС ~ ∆FАВ за двома кутами. Звідси АС : АВ = DС : FВ, тобто АС · FB = АВ · DC.

Додамо рівності і одержимо: АС (DF + FB) = АD · ВС + АВ · DC. Отже,  АС · ВD = АD · ВС + DС · АВ.

V. Закріплення та осмислення нового матеріалу

№1. На колі, описаному навколо рівностороннього трикутника АВС, взято довільну точку Х. Доведіть, що найбільший з відрізків ХА, ХВ, ХС дорівнює сумі двох інших.                                                                 

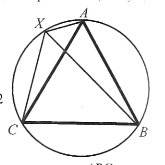                              Розв’язання.

      Нехай найбільший відрізок ХВ. Доведемо,

      що ХВ  = ХС + ХА. За теоремою  Птолемея

      ХВ ·АС = ХС · ВС + ХА · АВ.  За  умовою

 ∆АВС рівносторонній,  тому АВ =  ВС = АС.                

     Звідси ХВ · АС = ХС · АС + ХА · АС.  Отже,      

 ХВ = ХС + ХА.

 №2.Бісектриса кута А трикутника АВС перетинає описане коло в точці W. Доведіть, що АВ + АС < 2 АW.

                                    Доведення.

За   властивістю  бісектриси  САW  = WАВ. Звідси  WС  =  ВW.  

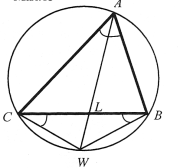                              За  нерівністю   трикутника  СW + WВ > ВС. 

                              Тоді  2 СW > ВС;  СW > ½ ВС. 

                                  Чотирикутник   АВWС  вписаний  у  коло,  то   

                              за  теоремою  Птолемея   АW · ВС = АВ · WС +                                

                                  + ВW · АС. Тоді АW · ВС = АВ · WС + WС · АС;

                                  АW · ВС = WС ( АВ + АС); 

                                  АW · ВС > ½ВС ( АВ + АС);

                                  АW > ½ ( АВ + АС);

                                  2 АW > АВ + АС.

VІ. Самостійна робота

Варіант 1.

1.                                     Дано: прямі АD і ВС  перетинаються                 

                                                    в точці О,  АВ || СD, ВО = 8см,                                                                                                          

                                                    СО = 4см, ОD = 10см.

                                         1) Довести, що трикутники подібні.

                                         2) Знайти АО.

                                         3) Знайти   .                       

                                         4) Знайти  .

2. Через точку S, яка лежить поза колом, проходять січні а і в. Січна а перетинає коло в точках N і М, а січна в, що проходить через точку О – центр кола,  в точках К і Р. Обчислити діаметр кола, якщо SР = 3см, МN = 4см, SN = 9см.

3. Сторони трикутника 48см, 24см, 56см. Знайти периметр подібного трикутника, якщо його найбільша сторона 7см.

4. У гострокутному трикутнику АВС ВD і АК – висоти. Доведіть, що DC · АС =  КС ·ВС.

 Варіант 2.

1.  Дано: КСРМ – трапеція, прямі КС і МР  перетинаються в точці А,  АС = 6 см,  СК = 4 см, КМ = 25 см.

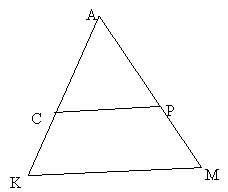
                                  1) Довести, що трикутники подібні.

                                          2) Знайти СР.

                                          3) Знайти  .                    

                                          4) Знайти .

2. Хорда СD і діаметр АВ перетинаються в точці М. Обчислити діаметр кола, якщо СD = 13см, МD = 7см і АМ = 14см.

3. Сторони трикутника 18см, 27см, 36см. Знайти периметр подібного трикутника, якщо його найменша сторона 36см.

4. У гострокутному трикутнику АВС висоти ВD і АМ перетинаються в точці О. Доведіть, що ВО · ОD = АО · ОМ.

VІІ. Підсумки уроку

Сьогодні на уроці ми познайомились та навчились використовувати теорему Птолемея, а також перевірили рівень засвоєння знань з вивчених тем.

Які будуть запитання по самостійній роботі.

На закінчення нашої роботи я хочу побажати, аби помилки, які ви допускаєте, не наводили вас до смутку, а були імпульсом для саморозвитку.

VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

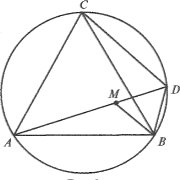
№1. У коло вписано рівносторонній трикутник АВС. Точка D належить ВС. Доведіть, що DА = DВ + DС.

                               Розв’язання.

     На рисунку у ∆АВС АВ = ВС = АС, точка D є ВС.  Отже, чотирикутник АСDВ вписаний у коло. Тоді АD · СВ = АС · ВD + DС · АВ за теоремою Птолемея. Звідси АD · СВ = СВ · DВ + +  DС · СВ. Отже,  АD =  DВ +  DС.

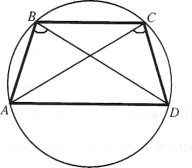
№2.Основи рівнобічної трапеції АВСD ( ВС || АD) a і b, бічна сторона с. Знайдіть діагональ.                                                                                       

                                            Розв’язання.  

На рисунку у  трапеції  АВСD  ВС || АD,  ВС = а, АD =  b, АВ =      = СD = с. Знайдемо АС.

   Оскільки трапеція АВСD рівнобічна, то АС = ВD і навколо неї можна описати коло. Тоді за теоремою Птолемея АС × ВD = АВ  · СD +  + АD · ВС.  Звідси     АС² = с² + аb.

    Відповідь: АС² = с² + аb.