Урок" Теорема Вієта"

Тема: «Теорема  Вієта »

Мета: сформувати вміння застосовувати теорему Вієта до розв’язування рівнянь; розвивати вміння відбирати й застосовувати потрібні знання та способи діяльності до досягнення мети; аналізувати та творче ставитися до праці

Тип уроку:  засвоєння нових знань і вмінь.

Обладнання та наочність: картки з друкованою основою, таблиця « Квадратні рівняння», підручник Алгебра 8клас ,В.Кравчук, М.Підручна, Г. Янченко.

Хід уроку

І. Організаційний етап

Привітання з учнями, перевірка готовності учнів до уроку.

ІІ. Актуалізація опорних знань.

І. Фронтальне опитування  «Мозковий штурм»(перевірка домашнього завдання)

1. Які рівняння називаються квадратними ?
2. Як називають числа a, b, с?
3. Яке квадратне рівняння називають зведеним?
4. Скільки коренів може мати квадратне рівняння?
5. Від чого залежить кількість коренів квадратного рівняння?
6. Чому дорівнює дискримінант квадратного рівняння?
7. Коли квадратне рівняння має два корені, один корінь, не має коренів?
8. Чи є правильним записаний дискримінант квадратного рівняння ?
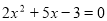
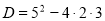9. За якими формулами знаходять корені квадратного рівняння?

ІІ. Установіть логічні пари.

А) D > 0                               1) Дійсних коренів немає

Б)  D = 0                                2) Два різні корені

     В)  D < 0                                3) Один корінь

Відповідь: А_________; Б_________; В__________.

ІІІ. Вивчення нового матеріалу

Інтелектуальна розминка.

1.Назвіть коефіцієнти квадратних рівнянь:

а)3х²+7х-8=0;

б)х²-11х+30=0;

в)х+х²=1;

г)2х²-9х+10=0;

д)х²+2х-24=0

2.З першого завдання виберіть рівняння, у яких а=1.

3. Робота в групах. Розв’язати  вибрані  рівняння та знайти суму та добуток коренів(  х²-11х+30=0;   х+х²=1; х²+2х-24=0)

«Мозковий штурм»

1. Чому дорівнює  коефіцієнт а?
2. Як називаються такі рівняння?
3. Чому дорівнює сума коренів?
4. Чому дорівнює добуток коренів?
5. Який висновок можна  зробити?

Сьогодні ми будемо розв’язувати  зведені квадратні рівняння за допомогою теореми Вієта.

А) Історична  хвилинка

Франсуа Вієт народився у 1540 році в місті Фонтене ле-Конт провінції Пуату. Отримав юридичну освіту. Він був широко освідченою людиною: знав астрономію, математику, вивчав твори класиків Архімеда і Діофанта.

Франсуа Вієт зробив вагомий внесок для розвитку математики, вважається

 «батьком сучасної алгебри». Написав першу у світі роботу з символічної алгебри. Він увів буквене позначення невідомих, саме від нього бере початок сучасна алгебраїчна символіка. Захопившись якоюсь математичною задачею, він міг працювати над нею іноді три доби без їжі і сну.

 У 1591 році він віднайшов формули, що пов'язують між собою корені квадратного рівняння і його коефіцієнти. Його висновок (у сучасних позначеннях) виглядає так: « Коренями рівняння (a +b) x-x²= ab  є числа  a і b».

Б)Означення  зведеного квадратного рівняння.

! Квадратне рівняння, перший коефіцієнт якого дорівнює 1, називають зведеним. Зведене квадратне рівняння записують у вигляді х²+px+q=0.

Зведене квадратне рівняння можна розв’язати за допомогою теореми Вієта.

Звернемось до рівнянь, які були розв`язані в завданні №3та занесемо результати в  таблицю

  Який  висновок можна зробити ?

З таблиці видно,що сума коренів кожного рівняння дорівнює другому коефіцієнту рівняння, узятому з протилежним знаком, а добуток коренів дорівнює вільному члену.

! Теорема Вієта(пряма теорема) . Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому із протилежним знаком, а добуток коренів дорівнює вільному члену.

Тобто. Якщо х₁, х₂- корені рівняння  х²+px+q=0,то х₁ +  х₂=-p, х₁ ∙  х₂= q

Приклад1. х²-2х-15=0, х₁ +  х₂=2,  х₁ ∙  х₂= -15, х₁=-3,х₂=5.

Чи можна за числами стверджувати, що вони коренями зведеного рівняння?

Приклад 2.Чи є числа 3 і 7 коренями рівняння  х²-10х+21=0?

Знайдемо суму коренів  3+7=10, сума дорівнює другому коефіцієнту рівняння, узятому із протилежним знаком, а добуток 3∙7=21 дорівнює вільному члену. Тому 3і 7 є коренями рівняння. Отже, маємо теорему обернену до  теореми  Вієта.

! Теорема обернена до теореми Вієта. Якщо сума двох чисел дорівнює - p, а їх добуток дорівнює q, то ці числа є коренями рівняння х²+px+q=0.

Увага!Використовувати теорему Вієта можна лише для квадратних рівнянь, які мають корені.

IV. Засвоєння  нових знань і вмінь.

Робота з підручником. Усна робота ст.178. №732-735.

Додаткові завдання. Робота в парах.

Один із коренів поданого квадратного рівняння дорівнює - 6. Знайдіть коефіцієнт k і другий корінь рівняння:1) х²-7х+ k=0;

2) х²+ k х-24=0;3)3х²+8х+ k=0;4)5х²+ k х+18=0.

V. Домашнє  завдання. Завдання за підручником. .   §3.п.22,№747,747,758.

Додаткове завдання.

1. Не обчислюючи корені рівняння х²+2х-15=0, знайдіть значення виразу

 (х₁ +х₂)- х₁∙х₂.

2.Корені  х₁, х₂ квадратного рівняння х²+9х+ q =0задовільняють умові

х₁=- 4х₂. Знайдіть х₁, х₂ і q .

VІ. Підсумки уроку

            « Мікрофон»

1. Сформулювати теорему Вієта для зведеного квадратного рівняння  .
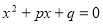2. Складіть зведене квадратне рівняння, коренями якого є числа - 4 і 6.
3. Сформулювати теорему Вієта для незведеного квадратного рівняння  .
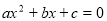4. Чому дорівнює сума і добуток коренів квадратного рівняння ?
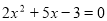5. Сформулювати теорему обернену до теореми Вієта.