Урок: "Трапеція. Середня лінія трапеції"

Предмет: ГЕОМЕТРІЯ  

Тема: Трапеція. Середня лінія трапеції.

Мета:

1. Сформувати поняття трапеції, окремих видів трапеції; домогтися засвоєння їх властивостей.

2. Розвивати логічне мислення, просторову уяву, кмітливість.

3. Сприяти формуванню цифрової грамотності, культури математичного мовлення, графічних зображень та математичних записів.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: креслярські інструменти, фрагменти презентації «Трапеція», «перфокарти», картонний набір геометричних фігур для створення геометричного малюнка «Будинок».

Хід уроку

І. Організаційний етап.

Налаштовування учнів на роботу на уроці

ІІ. Перевірка домашнього завдання.

1. Перевірка завдання, заданого за навчальним підручником.

2. Колективне розв’язування усних вправ (повторення).

ІІІ. Актуалізація опорних знань

Запитання для фронтальної бесіди

ІV. План вивчення теми

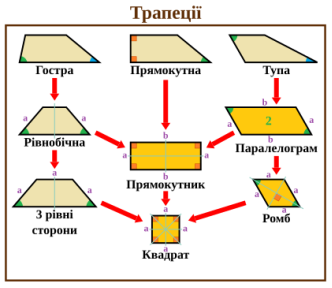
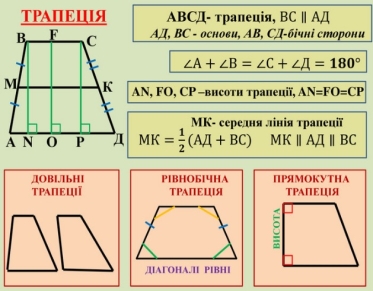
1. Означення трапеції та її елементів
2. Окремі види трапеції

а) прямокутна;

б) рівнобічна

       3. Властивості прямокутної трапеції

       4. Властивості рівнобічної трапеції

       5. Периметр трапеції

       6. Середня лінія трапеції

V. Закріплення нових знань і вмінь:

     1. Робота з навчальним підручником (Аркадій Мерзляк і ко. Геометрія 8 клас; § 8, ст. 44 – 47)

     2. Робота з «перфокартами»

         Додаткове завдання

VІ. Підбиття підсумку уроку (рефлексія).

      Фронтальне опитування учнів за ключовими частинами теми уроку.

      Оцінювання учнів за роботу на уроці.

VІІ. Домашнє завдання

1. Завдання за навчальним підручником: § 8; № 221, № 224, № 244
2. Додаткове завдання (опорна задача):

    У прямокутній трапеції діагоналі взаємно перпендикулярні. Кут між більшою діагоналлю і меншою бічною стороною дорівнює 30⁰. Довести, що менша діагональ дорівнює пів-сумі довжин основ /дов. за властивістю катета, що лежить проти кута 30⁰/.

І. Вправи для повторення.

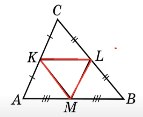1. У трикутника АВС точки K і L належать відповідно сторонам АC і ВС. Відрізок KL є середньою лінією якщо:

а) KL = АС;

б) KL АB ;   +

в) KL = АС, ∠ВLМ = ∠ВСA;

г) KL = BС, ∠AKМ = ∠АСB

 

2.  Скільки у трикутнику можна побудувати середніх ліній?

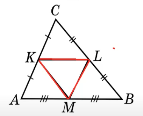                                           Учні відповідають, що «три»;

                                          одночасно виконується учнем побудова малюнка

                                                                               

                       

 

           3. Чому дорівнює периметр трткутника КМL, якщо сторони трикутника

           АВС  6см, 8см, 12с.  

          Периметр трикутника KМL дорівнює (6 + 8 + 12 ) : 2  = 13 (см)

 

ІІ. Актуалізація опорних знань

1. Пропозицція для учня (ІП):  скласти на дошці з геометричних фгур (вирізаних із цупкого кольорового картону) будинок; назвати кожну фігуру, до якого виду належать; зробити висновок, що до кількості використаних фігур кожного виду 
2. Учні класу доповрнюють відповідь назвою чотирикутника «ДЕЛЬТОЇД»
3. Вчитель замінює частину будинка (дах) на ішу геометричну фігуру – трапіцію. Запитує в учнів назву даного чотирикутника. Якщо учні не називають фігуру, називає вчитель і таким чином оголошується тема уроку.

ІІІ. Основна частина уроку

   Термін трапеція походить від давньогрецького τραπέζιον, trapézion, буквально «столик» — зменшувальна форма від τράπεζα («стіл», звідки й «трапеза»), утвореного з τετράς («чотири») + πέζα («нога, ребро»). У США і Канаді використовується термін trapezoid,   що походить від τραπεζοειδή («столоподібний»); перше задокументоване вживання цього терміна трапляється у Прокла (412—485 н. е.) у його коментарі до першої книги «Начал» Евкліда.

1. Переважною є позиція, що окрім двох паралельних сторін, трапеція повинна мати дві непаралельні сторони.
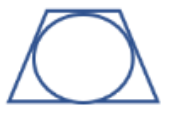2. Інша позиція, що до трапецій включають всі паралелограми (ромби, прямокутники і квадрати), оскільки вони мають дві пари паралельних сторін.

 

 

 

 

Дотичною називається трапеція, яка має 

вписане коло.

 

І варіант мал.                               ІІ варіант мал.

                                                

 

 

 

 

 

 

 

 

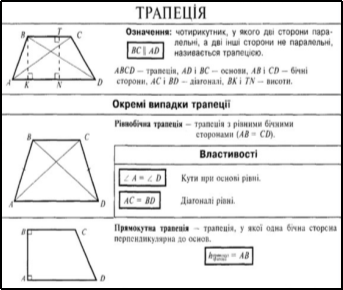
 У курсі школи розглядається, що трапеція – чотирикутник,  у якого дві сторони паралельні, а дві інші не паралельні.

Учні працюють за вчителем створюючи опорний конспект.

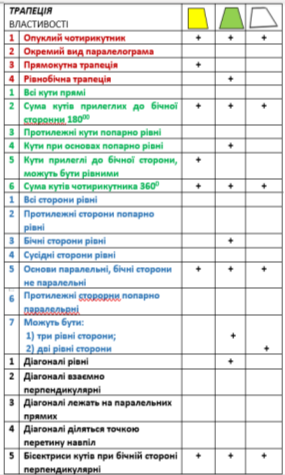
Властивості 

Для будь-якого опуклого чотирикутника такі властивості

еквівалентні, і кожна передбачає, що чотирикутник є трапецією:

•      Сума двох кутів, прилеглих до бічних ребер, дорівнює 180°.
•      Середня лінія трапеції паралельна основам і дорівнює їх півсумі.
•      Точка перетину діагоналей трапеції, точка перетину продовжень її бічних

      сторін та середини основ лежать на одній прямій.

•      Будь-яку трапецію можна побудувати за довжинами чотирьох сторін.
•      У рівнобічній трапеції:
  • бічні сторони рівні;
  • кути при основі, а також діагоналі рівні;
  • якщо діагоналі рівнобічної трапеції перпендикулярні, то висота такої; трапеції дорівнює середній лінії трапеції
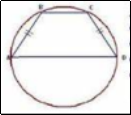•      Навколо рівнобічної трапеції можна описати коло.

 

 

 

 

 

 

 

 

 

 

 

 

  Опорний конспект який створюють учні на уроці.

Розв’язування вправ:

1. Закріплюють знання відповідаючи на запитання перфокартки
2.  Колективно доводять разом з вчителм властивість

          бісектрис кутів при бічній стороні трапеції:

1.     формулюється властивість бісектриси кута;
2.     формулюється властивість кутів прилеглих до бічної сторони трапецї (як внутрішні односторонні при паралельних прямих та січній);
3.     формулюється теорема про суму кутів трикутника, та обчислюється градусна міра кута, що утворився при перетині бісектрис кутів при бічній стороні трапеції

                                                 3. Вправа:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

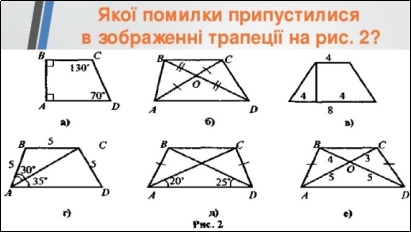
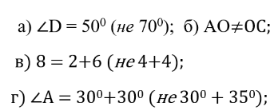
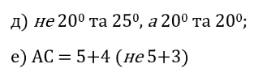
     Завдання для учня з особливими освітні

потребами

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

         

 

Деякі матеріали  до уроку були використані із ютуб ресурсів.