Урок "Теорема Піфагора"

 

 

 

 

 

 

Урок геометрії у 8 класі
"Теорема Піфагора".

 

 

 

 

 

 

 

 

 

 

 

з досвіду роботи
вчителя математики КЗ «Дергачівського ліцею № 4»
Дєєва Олександра
Миколайовича

 

 

 

 

 

 

 

 

2024 р.

 

 

 

Тема уроку: Теорема Піфагора

 Мета уроку: Познайомити учнів зі змістом і доведенням теореми Піфагора та наслідків з неї; показати застосування теореми при розв’язуванні задач. Розвивати логічне мислення школярів, формувати навики самооцінки, виховувати інтерес до історії математики.

 Обладнання уроку: комп’ютер, дошка, презентація «Теорема Піфагора»,              Тип уроку: урок формування знань та умінь.

 Очікувані результати:

 засвоєння учнями теореми Піфагора і наслідки з неї;

 вироблені уміння розв’язувати найпростіші задачі з теми;

 викликаний інтерес до біографії Піфагора як легенди і джерела дискусії;

 навчання учнів робити власні висновки.

 

План уроку

І. Організаційний момент.

Вчитель: Світ, що нас оточує, - це світ геометрії. Тому запрошую вас до його пізнання і нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір. Я надіюся на нашу співпрацю, свідоме засвоєння матеріалу уроку, зацікавленість до продовження роботи над мультимедійним проектом. Запишіть, будь-ласка, число, класна робота і тему уроку.

 У кулачному бою на  58-й Олімпіаді, яка проходила в 548 році до н.е. брав участь один із давньогрецьких математиків. Переказують, що через малий зріст судді не хотіли допустити його до змагань.

 - Можливо, - заперечив молодий вчений, - мій вигляд і не викликає у вас довір’я. Але я буду наносити удари з такою математичною точністю, що супротивникові стане жарко. Моя глибока віра в число – це моє життєве кредо.

 І він додержав свого слова – став чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах.

 То ж нехай його слова: „ Тимчасова невдача краща від тимчасової удачі” стануть девізом уроку.

 

 ІІ. Актуалізація опорних знань та умінь.

 

Вправа „Мозковий штурм”:

•          Який трикутник називається прямокутним?
•          Як називаються сторони АС і ВС прямокутного трикутника АВС?
  
  
  
  
  
  
  
   
•          Як називається сторона АВ прямокутного трикутника АВС?
•          Чи може у прямокутному трикутнику бути два прямих кути?
•          За малюнком запишіть властивості середніх пропорційних відрізків a і b.

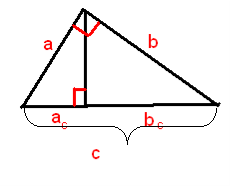
(1)
(2)

 

 

 

ІІІ. Вивчення нового матеріалу.

Додайте ліві та праві частини рівностей (1) та (2):

a² + b² = c ^. a_c + c ^. b_c; a² + b² = c(a_c + b_c). Але a_c + b_c = с. тому:
 

a² + b² = c²

 

це математичний запис теореми Піфагора:

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Перегляд презентації «Теорема Піфагора» (учень, який підготував презентацію, демонструє її на всі комп’ютери мережі та коментує слайди.

Запитання. А як за теоремою Піфагора знайти гіпотенузу трикутника, якщо відомі його катети?

.

Запитання. А як за теоремою Піфагора знайти катет трикутника, якщо відомі його гіпотенуза і катет?

 .

Наслідок: катети прямокутного трикутника менші за гіпотенузу.

Задача 1. За малюнком знайдіть гіпотенузу трикутника.

 

 

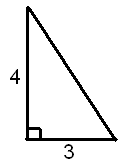
= 5

 

 

 

 

 

 

 

 

Задача 2. За малюнком знайдіть катет трикутника.

 

 

 

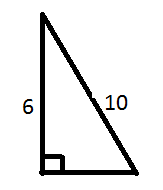
=8

 

 

 

 

 

Трикутники, у яких сторони пропорційні до чисел 3, 4, 5, називаються єгипетськими.

ІV. Первинне закріплення.

За малюнками знайдіть невідомі сторони прямокутних трикутників:

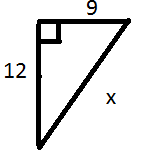
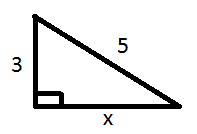
V. Розв’язування задач.

Задача 1. У рівнобедреному трикутнику АВС з основою АС = 16 см висота BH = 6 см. Знайдіть бічну сторону.

 

 

 

 

 

 

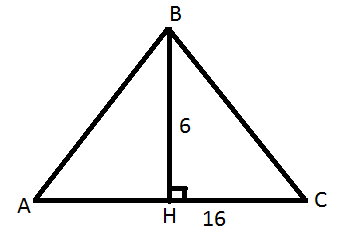
Задача 2. Сторони прямокутника 8 см і 15 см. Знайдіть його діагональ.

 

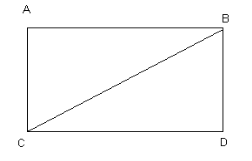
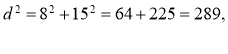
d = 17 см.

VІ. Тестування.

Комп’ютерний тест.

VІІ. Підведення підсумків уроку.

1. З чим ми познайомились на уроці?
2. Що ми навчилися робити?
3. Як звучить теорема Піфагора?

VІІІ. Домашнє завдання.

Вивчити теоретичний матеріал на с. 140-141. Розв’язати №№ 1(б), 2(а), 4 на с. 143.

 

Додаткові матеріали.

Історична довідка про Піфагора.

 Піфагор – один із найбільш знаменитих учених за всю історію людства. Він був не лише вченим і засновником першої наукової школи. Ця унікальна людина була і засновником першої наукової школи. Ця унікальна людина була і „володарем душ”, і проповідником власної „піфагорської” етики, і великим філософом. Піфагор виховав у людства віру в могутність розуму, переконаність у можливості пізнання природи, впевненість у тому, що ключем до таємниці світопобудови є математика.

 

 Історія теореми Піфагора.

Адже була відома у Вавілоні ще за 1500 років до народження Піфагора. Можливо, що тоді ще не знали її доведення, а співвідношення між гіпотенузою і катетами було встановлено дослідним шляхом на основі вимірів. Піфагор, очевидно, знайшов доведення цього співвідношення. Збереглася давня легенда, що на честь такого відкриття Піфагор приніс у жертву сто биків, хоча за іншими версіями вчений був непримиренним противником жертвування тварин, особливо великої рогатої худоби.

 В різних джерелах теорему Піфагора називають „теорема нареченої”, „ослиний міст”, „Піфагорові штани”.    

       

  Математику та літературу іноді ставлять на протилежних полюсах людського знання. Проте мости між літературою й точними науками ніколи не розводилися, адже людський інтерес не можна відділити від емоцій, а „сухі” формули не ізольовані від гарячого „випромінювання” людських почуттів.

 Сонет відомого німецького поета ХІХ століття Адельберта фон Шаміссо є прикладом гармонійного поєднання поезії з геометрією.

Як Істину відкрив – сіять їй вічно,

Вона нам – найнадійніша опора:

Так в древній теоремі Піфагора

Й донині бездоганно все й логічно.