Урок "Тригонометричні функції числового аргументу"
Тема уроку: Тригонометричні функції числового аргументу.
Мета уроку: повторити, систематизувати й узагальнити знання учнів з теми; розвивати логічне мислення, пізнавальну діяльність, вміння застосовувати властивості тригонометричних функцій до побудови графіків;
виховувати наполегливість, самостійність, увагу, охайність у виконанні малюнків.
Тип уроку: Урок узагальнення і систематизації знань.
Обладнання: комп’ютери, таблиця властивостей, картки-завдання,
ХІД УРОКУ
І.Перевірка знань учнів
- 2 учня біля дошки:рина
- Знайти період функції у = sin4x – cos4x і побудувати її графік.
Розв’язання:
Спростимо функцію у = sin4x – cos4x = (sin2x – cos2x) (sin2x + cos2x) = sin2x – cos2x = – (cos2x – sin2x) = – cos2x. Визначаємо період функції за формулою Т = 
, де k – коефіцієнт при х. Отже Т = 
. Графік функції зображено на рис.1.
-
Знайти період функції
.
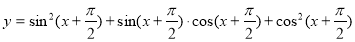Розв’язання:
Для спрощення функції будемо використовувати формули зведення.
= 
=
. Отже період функції Т =
- всі інші учні виконують тестову роботу на комп’ютері:
Варіант 1. Варіант 2.
1.Знайти область визначення функції 1.Знайти область визначення функції
у = sin3x y = cos2x
a) (-3; 3); б) (-3; +); a) (-3; 3); б) (-3; +);
в) (-; 1); г)(- ; + ). в) (-; 1); г)(- ; + ).
2.Знайти область значень функції 2.Знайти область значень функції
y = 3cosx у = 2sinx
a) (-1; 1); б) (-2; 2); a) (-1; 1); б) (-2; 2);
в) (-3; 3); г)(- ; + ). в) (-3; 3); г)(- ; + ).
3. Визначити парна чи непарна 3. Визначити парна чи непарна
функція y = 2tgx функція y = 3ctgx
a) парна; б) непарна. a) парна; б) непарна.
4. Знайти період функції 
4. Знайти період функції 
a) Т = 2; б) Т = ; a) Т = 2; б) Т = ;
в) Т = 4; г) Т = 
. в) Т = 4; г) Т = 
.
5. Чому дорівнює найбільше 5. Чому дорівнює найбільше
значення функції 
значення функції y = 4sin3x
a) y = 4; б) y = 
; a) y = 4; б) y = ;
в) y = 3; г) y = 1. в) y = 3; г) y = 1.
6. Чому дорівнює найменше 6. Чому дорівнює найменше
значення функції 
значення функції 
a) y = 
; б) y = -1; a) y = ; б) y = -1;
в) y = -2; г) y = 
. в) y = -2; г) y = 
.
Відповіді на тести.
Варіант 1 Варіант 2
|
1 |
2 |
3 |
4 |
5 |
6 |
|
г |
в |
б |
в |
б |
в |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
г |
б |
б |
г |
а |
а |
ІІ. Актуалізація опорних знань.
Презентація «Перетворення графіків функцій виду 
ІІІ. Розв’язування вправ. Робота в групах:
І група – синуси;
ІІ група – косинуси;
ІІІ група – тангенси;
ІV група – котангенси.
Завдання групам:
а) створити рекламу для графіка своєї функції
б) побудувати графік функції, вказати її властивості:
- область визначення;
- множину значень;
- період функції;
- зростання (спадання);
- набування додатних (від’ємних) значень;
- нулі функції;
- найбільше (найменше) значення функції.
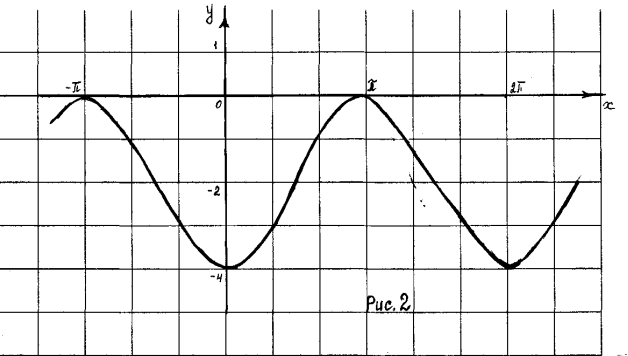
І група – 
; (рис.2)
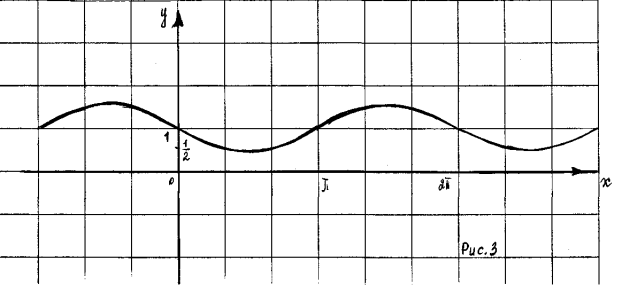
ІІ група – 
; (рис.3)
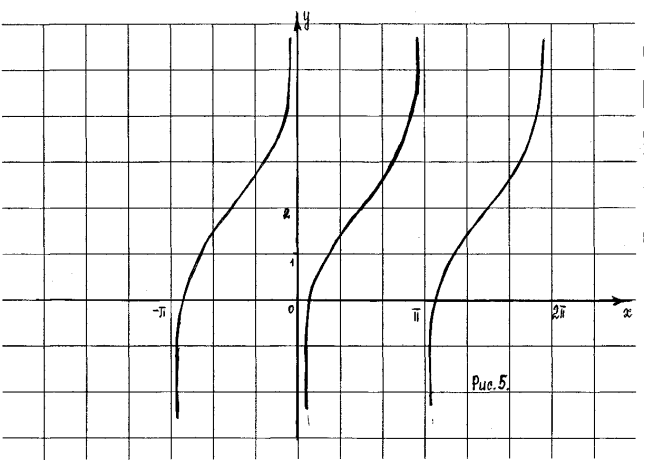
ІІІ група – 
; (рис.5)
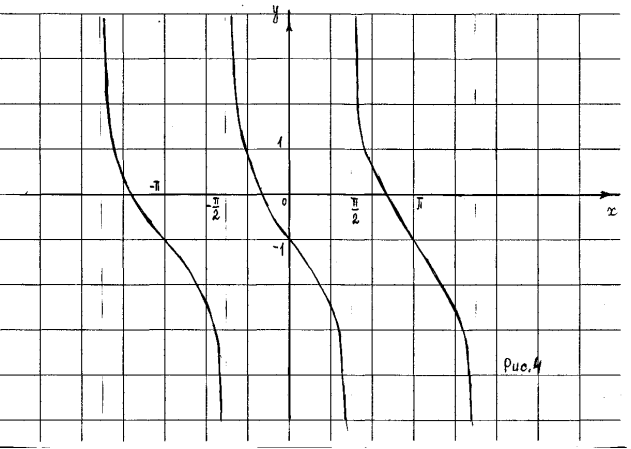
ІV група – 
(рис.4)
Розв’язання записуються в таблицю:
|
Властивість |
Функції |
|||
|
|
|
|
|
|
|
1.Область визначення |
(- ; + ) |
(- ; + ) |
х(- ; + ) x n, nZ |
х(- ; + )
x |
|
2.Множина значень |
(-4; 0) |
( |
y(- ; + ) |
y(- ; + ) |
|
3.Період функції |
Т = 2 |
Т = 2 |
Т = |
Т = |
|
4.Проміжки зростання |
х2n; + 2n nZ |
х nZ |
х(- ; + ) |
- |
|
5.Проміжки спадання |
х-+2n;2n, nZ |
х nZ |
- |
х(- ; + ) |
|
6.Набуває додатних значень |
- |
х(- ; + ) |
показують на малюнку |
показують на малюнку |
|
7.Набуває від’ємних значень |
х(- ; + ) |
- |
показують на малюнку |
показують на малюнку |
|
8.Набуває нульових значень |
х = +2n, nZ |
- |
показують на малюнку |
показують на малюнку |
|
9.Набуває найбільше значення |
у = 0 при х = +2n, nZ |
у =
х = |
- |
- |
|
10.Набуває найменше значення |
у = - 4 при х = 2n, nZ |
у =
х = |
- |
- |
+
)
при
+ 
при
+
ІV. Підсумок уроку.( метод мікрофон)
- Від якого компонента залежить період функції?
- Від якого компонента для функцій у = sinx, y = cosx залежить множина їх значень?
- Чи відносяться до неперервних функції y = tgx, y = ctgx?
- Які з тригонометричних функцій мають найбільше та найменше значення?
V.Домашнє завдання:
Повторити п.27-30 с.171-184, виконати №28 с.196
про публікацію авторської розробки
Додати розробку