Урок у 5 класі на тему: "Дії з десятковими дробами"

Дії з десятковими дробами

Працюй для того, щоб насолоджуватись.

Ж.Ж. Руссо

 

.

 

Мета:

• узагальнити знання про десятковий дріб, удосконалити вміння порівнювати, додавати і віднімати десяткові дроби, навички запису іменованих чисел за допомогою десяткових дробів;
• розвивати пізнавальну активність, культуру мови, сприяти формуванню умінь переносу знань у нову ситуацію;
• виховувати відповідальність, акуратність і самостійність, організованість;
• коригувати довгострокову пам’ять, увагу

Тип уроку: урок узагальнення та систематизації знань, умінь та навичок

Обладнання: засоби мультимедіа, слайдові презентація до уроку, наочний матеріал, картки з завданнями

 

 

Хід уроку

I. Організаційний момент

                                            Пролунав  дзвінок,

                                            Починаємо урок.

                                            Працюватимемо старанно,

                                            Щоб почути у кінці,

                                            Що у нашім п’ятім класі

                                            Діти – просто молодці.

Сіли тихесенько Подивились чи все є у вас до  уроку усміхнулись один одному. ПОЧНЕМО

 Мотивація навчальної діяльності.

Учитель. На попередніх уроках ви навчилися до­давати та віднімати десяткові дроби. Сьогодні ми по­винні пригадати й повторити, що вже вивчили. Тож об'єднаємося в ДВІ команди — «Сміливці», «Винахідники».

.

Математичний бій покаже, яка команда є згуртованішою, кмітливішою, розумнішою. У бій!

III. Актуалізація опорних знань.

1 Старт

 

Сьогодні ми подорожуємо країною »десяткові дроби» Прибувши до країни необхідно привітатися з господарем

1. На дошці написані дроби  необхідно їх прочитати з умовою : якщо дріб вірно прочитано  то плескаємо в долоні  якщо ні – тиша 36 011 8497 0005 25 17 163295  68 04  204 567
2. 2.Підкресли букви, які позначають істинні висловлення

: 43,04 > 43, 10 (А); 18,263 > 18,2631 (М); 0,5 > 0,49 (Д); 45,20 = 45,2 (Б); 4,586 < 4,57 (Р); 4,241 > 4,25 (Н); 40,05 > 41 (К); 342,05 < 342,4 (И); 34,25 < 35,25 (О); 0,21452 < 0,21352 (Т); 68,34 > 68,345 (Ш). Відповідь. Дроби.

 

2 ТЕОРЕТИЧНА

Інтерактивна вправа «Мікрофон»

Давайте згадаємо, все що знаємо про десяткові дроби:

1. Як називається дріб  записаний за допомогою коми?
2. Які звичайні дроби можна записати у вигляді десяткових дробів?
3. Як порівняти десяткові дроби з різними цілими частинами?
4. Як порівняти дроби з рівними цілими частинами?
5. Як округлити десяткові дроби?
6.  Як додати десяткові дроби?

Крок правила	Приклад
Зрівняти в доданках число цифр після коми	103+12407
Записати доданки один під одним так щоб кожний розряд доданків співпадав	10300 121407
3)Додати отримані числа як додають натуральні	+10300    121407   131707
4)Поставити в сумі кому під комами	+10300    121407   131707

3 ЗАДАЧНА

Задача. Швидкість човна проти течії дорівнює 9,5 км/год, а швидкість течії – 1,6 км/год. Обчисліть швидкість човна в стоячій воді і за течією річки

Задача  Одна сторона трикутника дорівнює 4,7 см., друга – на 5,9 см. довша від першої, а третя – на 3,7 см. довша від другої. Знайдіть периметр трикутника

Вироблення навичок розв’язувати задачі.  «Практикум».

1. Екологія За 2010 рік у Прилуцькому районі самовільно було знищено лісових насаджень на суму 288,81 тис. грн. А в 2011 році протягом січня місяця, було знищено насаджень на суму 23,2 тис. грн. Який загальний збиток від вирубки зелених насаджень?

(288,81+23,2=312,01 тис.грн.)

2. Місто Маріуполь скидає неочищених стічних вод - 253,83 млн.м³, а Дніпропетровськ - 188,2 млн. м³. На скільки млн.м³ Маріуполь викидає більше шкідливих речовин, ніж Дніпропетровськ? 

 (253,83-188,2=65,63 млн..м³).

3. Запоріжжя скидає неочищених вод - 65 млн. м³;
   Київ скидає – 29 млн. м³; Скільки шкідливих речовин викидають у воду, всі перераховані міста разом?

 (253,83+188,2+65+29=536,03 млн..м³). 

 

4ЛОГІЧНА

5ПІЗНАВАЛЬНА Задача  У процесі росту сосна ввібрала з повітря 1,84т вуглекислого газу, із землі 0,55т води, і 0,03т мінеральних речовин і виділила в повітря 1,42 т кисню. На скільки збільшилась маса сосни?

Розв’язання:

1) 1,84 + 0,55 +0,03 = 2,42 (т)

2) 2,42-1,42=1(т)

Відповідь: 1 т.

2) Вчитель: Виховний момент.

а) Бережливе ставлення до природи, зокрема дерев.

в) Перебуваючи в лісі ви повинні поводитись так, наче прийшли в гості до близького друга, поважати, берегти все, що там росте, не засмічувати лісу, не зривати оберемків квітів, не ламані гілок. Все це зводиться до запам'ятовування прості істини: природа, а отже, і ліс, не безконечні, вони вичерпні. Природа чуйна і щедра. Вона віддячить за наше добро сторицею.

Задача  Жителі каїни ДД полюбляють і знають географію Назвіть відомі вам океани

Назва океану	Площа млн. кВ км
Тихий	179   7
Атлантичний	93   4
Індійський	74    9
Північний Льодовитий	13     0
Світовий	361    0

6СПОРТИВ VII. Фізкульт - пауза

Учитель. Хто там, хто там притомився?

І на парту нахилився?

Учень (продовжує). Треба дружно нам всім встати,

Фізкульт-паузу почати.

Руки вгору підніміть

І тихенько опустіть.

Руки вгору, руки в боки

І зробіть чотири кроки.

Раз, два, три, чотири.

Раз, два-поринаємо,

Три, чотири - - виринаємо,

П'ять, шість - на воді

Кріпнуть крильця молоді.

Сім, вісім - всі сідаємо

І роботу починаємо.

VІІІ. Розв'язування вправ

   2. Гра «Вірю – не вірю» (з використанням сигнальних карток: зелена-так, червона-ні)

1. Чи вірите ви, що число 5,07 є  десятковим дробом?
2. Чи вірите ви, що число 0,9 менше за 1,01?
3. Чи вірите ви, що сума чисел 3,02 і 6,8 дорівнює десяти?
4. Чи вірите ви, що десятковий дріб не зміниться якщо справа до нього дописати нулі?
5. Чи вірите ви, що12,2000=12,2?
6. Чи вірите ви, що під час додавання не звертають увагу на кому?

 

 

7 ІСТОРИЧНА  

- Сучасні знаки «+» і «-» стали загальновживаними, починаючи із XVI ст.. Уперше ці знаки з’явилися в праці німецького математика Я.Відмана (1489 р. – I половина XVI ст.). Вважають, що спочатку знак « - » використовували для позначення недостачі, збитку в торгівлі, а знак «+» для позначення прибутку.

 У різних народів знаки додавання і віднімання спочатку мали неоднакову форму. Так, у стародавніх єгиптян знак «+» нагадував зображення двох ніг, що рухаються вперед, а знак « - » був схожий на зображення двох ніг, що рухаються назад.

 

 

- Десяткові дроби були відомі з давніх-давен. У деяких країнах Азії вони застосовувалися ще до нашої ери.

У XV ст. знання про десяткові дроби значно розвинув провідний учений найкращої на той час у світі Самаркандської астрономічної обсерваторії аль Каші. У творі «Ключ до арифметики» (1427 р.) він дав правила дій над десят­ковими дробами. Десяткові дроби аль Каші зображав різними способами: ці­лу частину відокремлював вертикальною рискою або писав її іншим кольо­ром, або надписував над цифрами назви розрядів.

Згодом десяткові дроби з'являються і в Європі. У 1585 році вийшла праця про десяткові дроби нідерландського інженера Симона Стевіна.

 

Кому, як знак дробовості, запропонував англійський математик Непер у 1617 році. Але ще раніше її застосовували німецький учений Кеплер та італійський астроном Маджіні.

 

 

Ще у III ст. до н.е. в Китаї використовували десяткові дроби. А в XV ст. повну теорію десяткових дробів розробив самаркандський астроном Джемшід ал-Каші в трактаті «Ключ до арифметики». Можливо, що ал-Каші не знав, що десяткові дроби здавна застосовувалися в Китаї. Сам він вважав їх своїм винаходом.

Важливий крок вперед зробив французький вчений Франсуа Вієт, що відображено в його праці «Математичний канон», опублікованій у 1579 р. в Парижі. Записуючи десяткові дроби, інколи він відділяв цілу частину від дробової вертикальною рискою, інколи цифри цілої частини зображав жирним шрифтом, або цифри дробової частини писав меншими цифрами.

З інших позицій підійшов до десяткових дробів С.Стевін. У праці «Десята» (1585 р.) Стевін ввів десяткові дроби, розробив для них правила арифметичних операцій, одночасно запропонував десяткову систему грошових одиниць, мір і ваги.

 

8ПРАКТИЧНА

Відніми дроби, розташовані на пелюстках квітки

Визначте назву самої великої у світі черепахи, виконавши завдання за схемою.

Схема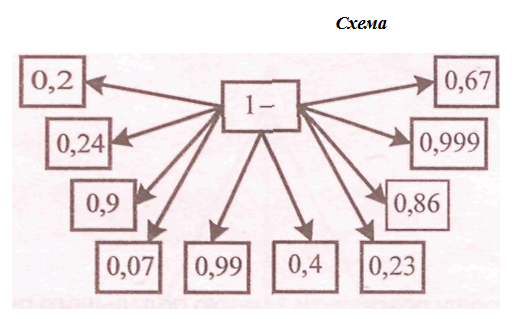

Ключ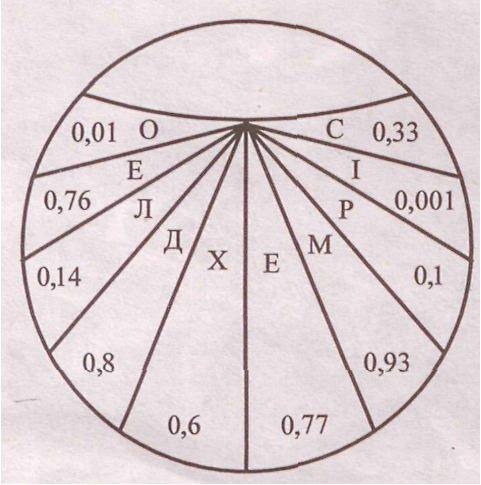

Відповідь. ДЕРМОХЕЛІС.

2. Дітям віком 13-15 років вагою 43-50 кг кожного дня необхідно вживати: білків - 95.94 г, жирів - 84,87 г , вуглеводів - 383,76 г. Скільки повинен вживати кожен з вас білків, жирів , вуглеводів разом.

                                                                    ( В . 564,57)

 

 

Підсумок уроку

Подайте дроби в порядку спадання

2,5	2,15	2,7	2,05	2,001	2,54	2,62
О	Д	М	Ц	І	Л	О

МОЛОДЦІ

Інтерактивний прийом «Мікрофон»

Наша подорож завершена. Чи сподобалась вам ця своєрідна мандрівка у     місто десяткових дробів? Яка зупинка вам найбільше запам’яталась? Що вам вдавалось важко? Чи досягли ви очікуваних результатів?

Вчитель робить підсумок досягнення мети.

 

 

Учні висловлюють свої думки щодо очікуваних результатів уроку, чи отримали вони знання та вміння, які запланували. Вчитель спонукає учнів до самооцінки:

1) Мені все було зрозуміло, я впорався зі всіма самостійними завданнями.

2)  Мені було зрозуміло майже все, але під час виконання самостійних завдань я припустився кількох помилок.

3) Мені було важко виконувати запропоновані вправи, але я розумію, що причина-недостатність знань; цей недолік я буду намагатись виправити.

VII. Домашнє завдання.

п. 27, №№ 772 (1-8); 774 (1-3); 776 (1-6); 778. Скласти 4 – 5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додатково

 

З історії виникнення десяткових дробів

Десяткові дроби були відомі з давніх-давен. У деяких країнах Азії вони застосовувалися ще до нашої ери.

У XV ст. знання про десяткові дроби значно розвинув провідний учений найкращої на той час у світі Самаркандської астрономічної обсерваторії аль Каші. У творі «Ключ до арифметики» (1427 р.) він дав правила дій над десят­ковими дробами. Десяткові дроби аль Каші зображав різними способами: ці­лу частину відокремлював вертикальною рискою або писав її іншим кольо­ром, або надписував над цифрами назви розрядів.

Згодом десяткові дроби з'являються і в Європі. У 1585 році вийшла праця про десяткові дроби нідерландського інженера Симона Стевіна.

 

Кому, як знак дробовості, запропонував англійський математик Непер у 1617 році. Але ще раніше її застосовували німецький учений Кеплер та італійський астроном Маджіні.

2

                  V.     Історична довідка.

 Сучасні знаки «+» і «-» стали загальновживаними, починаючи із XVI ст.. Уперше ці знаки з’явилися в праці німецького математика Я.Відмана (1489 р. – I половина XVI ст.). Вважають, що спочатку знак « - » використовували для позначення недостачі, збитку в торгівлі, а знак «+» для позначення прибутку.

 У різних народів знаки додавання і віднімання спочатку мали неоднакову форму. Так, у стародавніх єгиптян знак «+» нагадував зображення двох ніг, що рухаються вперед, а знак « - » був схожий на зображення двох ніг, що рухаються назад.