Урок узагальнення знань з теми "Призма". Геометрія 11 клас. Метод проектів.
Завдяки участі в проекті учні отримують вміння працювати з різноманітними джерелами інформації, здобувають знання та досвід, необхідний для подальшого життя. Вчаться на практиці використовувати набуті знання. Переконуються в тому, що математика потрібна в повсякденному житті.
- Åਧ¼á.docx docx
- ä«ñáΓ«¬ 1.pptx pptx
- ä«ñáΓ«¬ 3.1.pptx pptx
- ä«ñáΓ«¬ 3.2.pptx pptx
- Показати всі файли
Проект «Призма. Пряма і правильна призма. Площа бічної та повної поверхонь призми. Об’єм призми. »
Шкварок Л. М., вчитель математики, Іванківська ЗОШ І-ІІІ ст., Борщівський р- н, Тернопільська обл.
Учасники проекту: учні 11 класу.
Тип проекту: навчальний, інформаційно-дослідницький та практично- орієнтований.
Термін виконання: 3 тижні
І. Актуальність проекту як навчальної технології.
Проектне навчання сприяє розвитку учня як творчої і активної особистості, створює ефективні умови для розвитку компетенцій. Учні набувають досвіду розв’язування реальних проблем життя у навчально- виховній діяльності. Робота над проектом розвиває творчі здібності, уяву. Створює умови для розвитку індивідуальних і творчих сил та здібностей школярів за інтересами та їх реалізації, забезпечує можливість постійного самовдосконалення
ІІ. Мета і завдання.
- Узагальнити і систематизувати теоретичні знання учнів з теми.
- Показати практичне застосування теми на прикладних задачах із життя.
- Активізувати пізнавальну діяльність учнів сприяти розвитку інтелектуальних і творчих їх здібностей
- Розвивати навички мислення, формувати вміння генерувати ідеї, розвивати пам’ять та обчислювальні навички
- Створити і оформити тематичну презентацію та публікацію .
- Формувати математичну мову
- Надати можливість продемонструвати власні здібності і вміння переконувати.
- Навчити учнів працювати з додатковою літературою.
ІІІ. Етапи реалізації :
- Поділ класу на групи .
- Отримання завдання.
- Визначення джерел інформації.
- Вибір засобів презентації.
- Підбір матеріалу, його аналіз і складання плану роботи, розподіл обов’язків.
- Створення презентації на ПК.
- Оформлення презентації і публікації.
- Попередній перегляд презентації і публікації вчителем.
- Корекція і остаточний варіант.
- Презентація проекту перед учнями класу.
Очікувані результати
- Повторення теоретичних знань з теми.
- Розвиток життєвих, соціальних компетентностей.
- Розвиток комунікативних навичок.
- Виховання почуття відповідальності за спільну роботу.
Даний проект складається з трьох міні - проектів.
Захист проектів
Призма. Пряма і правильна призма. Площа бічної та повної поверхонь призми.
Мета: домогтися засвоєння учнями означення призми, прямої і правильної призми, формул для обчислення площі бічної і повної поверхонь призми та її об´єму.
Виховувати здатність логічно й аналітично мислити, уважність і акуратність під час виконання графічних робіт.
Розвивати просторову уяву та математичну мову.
Тип уроку: засвоєння нових знань.
Обладнання: таблиця, ноутбук.
Девіз уроку:” Разом учитися не тільки легше й цікавіше, але й значно ефективніше”.
Полат Е. С.
Хід уроку
І. Організаційний етап.
ІІ. Перевірка домашнього завдання.
За ключовими моментами домашніх вправ учитель ставить запитання учням.
ІІІ. Мотивація навчальної діяльності.
Учитель. Щоб успішно навчатися математики, оволодівати міцними математичними знаннями, необхідно бачити об´єкти в різноманітності їх властивостей і відношень, уміти діяти подумки, тобто мати добре розвинену уяву. А також мати достатню волю, розвинену увагу, добру пам´ять і кмітливість. Але ці вміння і якості формуються і міцніють у процесі наполегливого вивчення математики.
IV. Вивчення нового матеріалу (Додаток 1).
Щоб дізнатися, про що піде мова на сьогоднішньому уроці, розгадаємо кросворд( слайд№1,№2)
Отже,тема сьогоднішнього уроку…(Слайд №3,№4, №5)
Вчитель.Як відомо,в стереометрії не звертають уваги на те,з чого виготовлені предмети. Нас цікавить форма тіл та їх розміри. А якої форми тіла найбільш поширені в навколишньому середовищі?
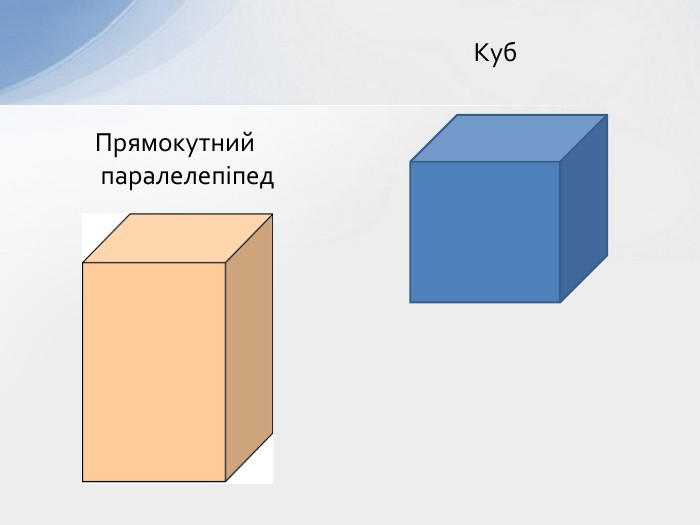
Учні. Прямокутного паралелепіпеда, куба.(Слайд №6)
Вчитель. Наведіть приклади
Учні. Сірникова коробка,кришка стола,балки,форма будинків та кімнат,цеглина…(Слайд №7, №8)
Вчитель. У названих вами предметів схожа форма: всі вони мають паралельні та рівні основи, а бічні грані-прямокутники або квадрати.
Як же можна утворити таку форму? Паралельно переміщувати прямокутник або квадрат уздовж певної лінії.(Слайди № 9-11)
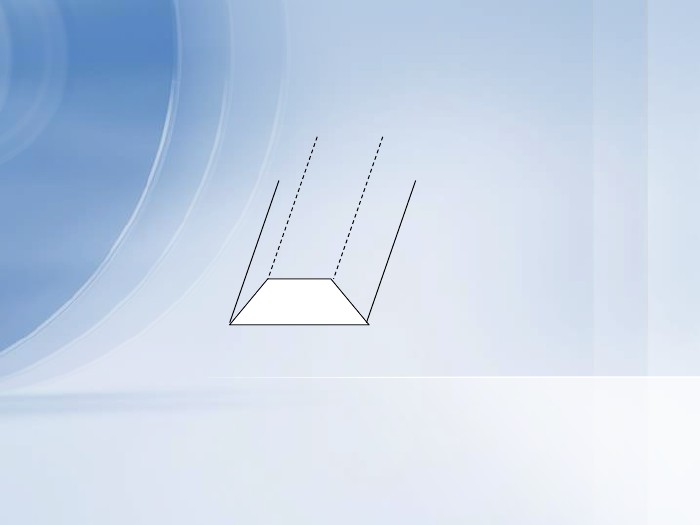
Вчитель. А якщо рухати не прямокутник, а,наприклад, трапецію, паралелограм або трикутник? Яка буде форма утвореного тіла? Назвіть предмети довкілля такої форми
Учні. Олівець, залізничний насип, трикутні кутові шафи … (Слайд №12)
Вчитель. Щоразу обговорюємо з учнями яка саме фігура рухалася. Що спільного у цих тіл?
Учні. Поверхня всіх цих тіл складається зі скінченної кількості многокутників: дві грані – рівні n-кутники, а решта n граней – паралелограми.
Вчитель. Такі тіла називають призмами. У дослівному перекладі з грецької слово призма означає обпиляне тіло.
Міні - проект №1
Демонструє група математиків (Додаток 2)
Тема. Призма . Формули для обчислення бічної, повної поверхні та об’єму призми.
План
-
Теоретичний матеріал
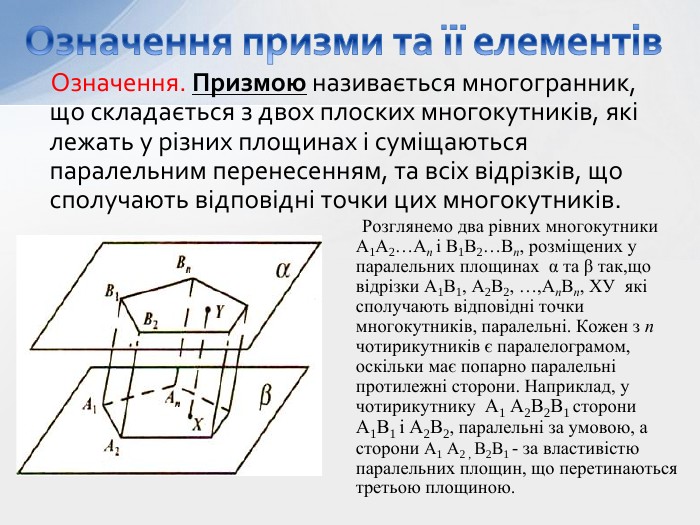
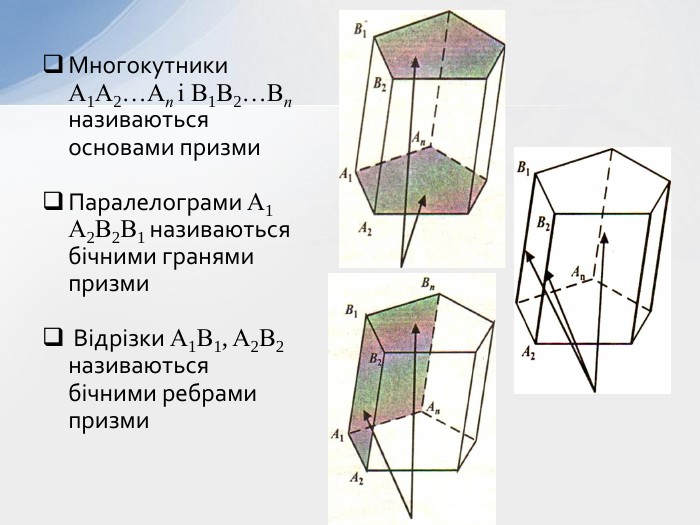
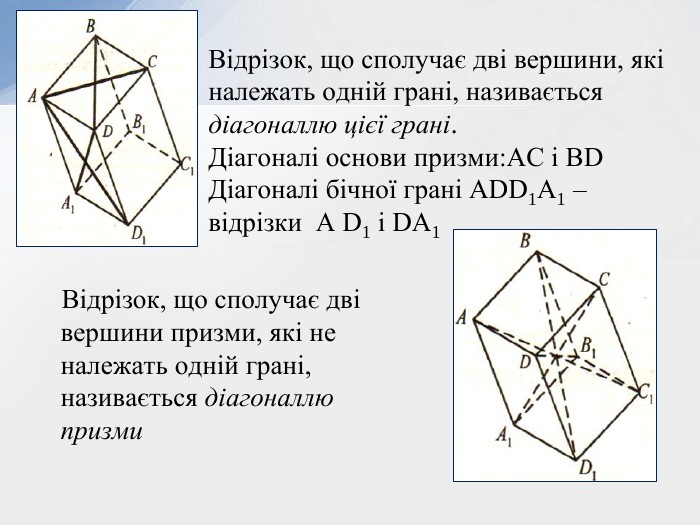
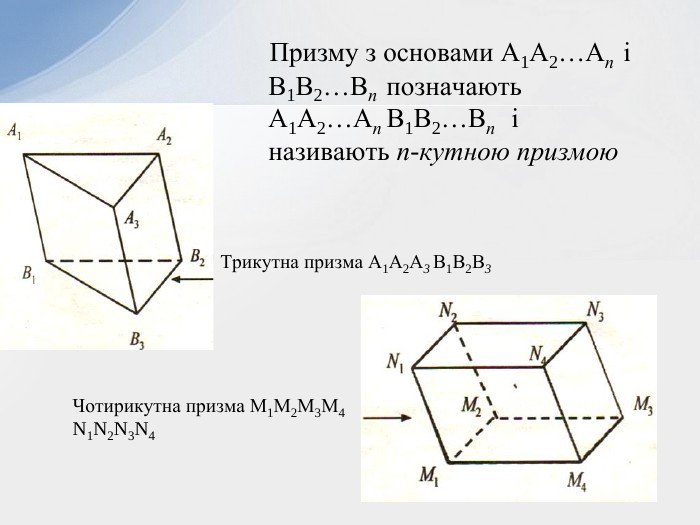
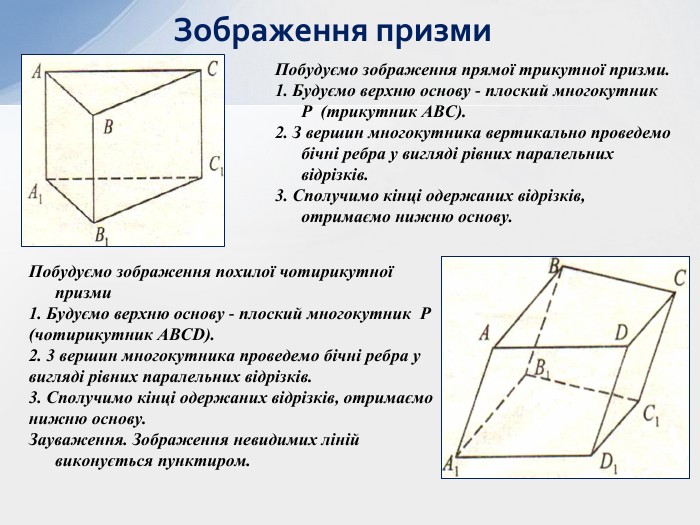
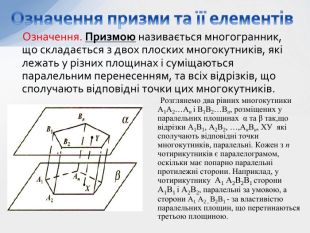
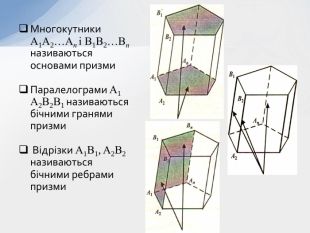
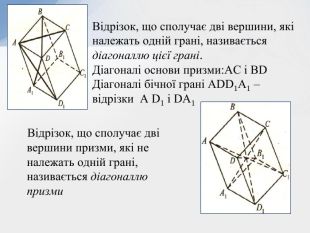
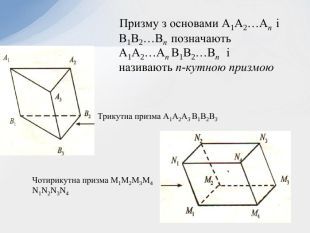
- Означення призми та її елементів
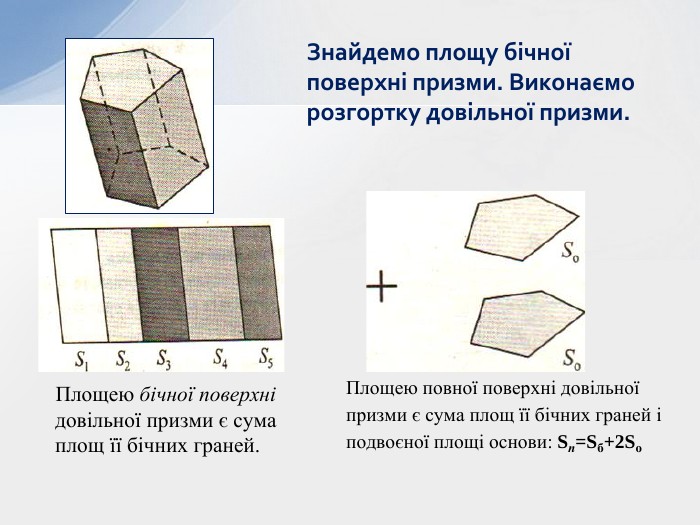
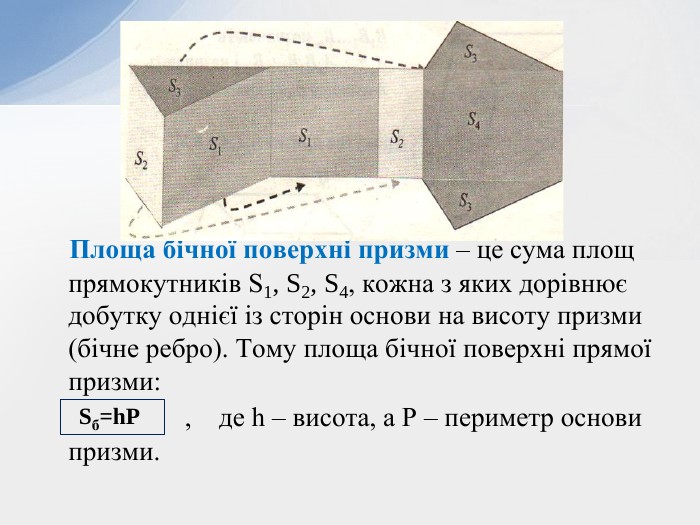
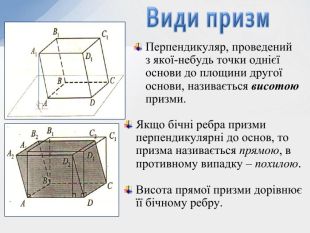
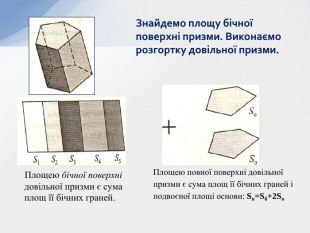
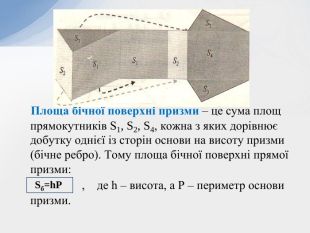
- Теорема про площу бічної поверхні призми.
- Теорема про площу бічної поверхні похилої призми
- Формули для обчислення площі поверхні та об’єму довільної призми.
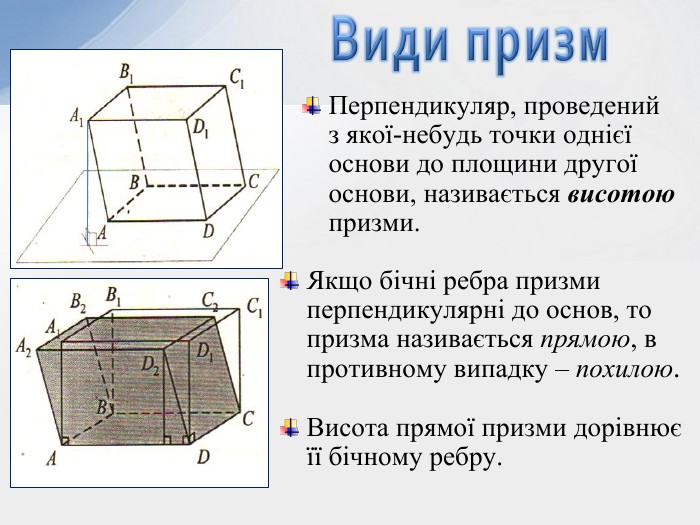
- Паралелепіпед як окремий вид призми.
- Задачі з математики , в яких використовується поняття призми.
Міні - проект №2
Демонструють групи істориків , будівельників, спортсменів. (Додаток 3)
Тема. Застосування формул на обчислення повної, бічної поверхні призми до розв’язування задач прикладного змісту.
План
- Дослідити чим зумовлена прямокутна система побудови архітектурних форм.
- Представити зображення історичних споруд,що мають форму призми.
- Вияснити, які інструменти та деталі мають призматичну форму.
- Дослідити, які спортивні знаряддя мають призматичну форму.
- Підібрати задачі ,які виникають у повсякденному житті, і для роз’язування потребують математичних знань.
Міні-проект №3
Демонструють групи біологів,хіміків,пасічників. (Додаток 4)
Тема. Розв’язування задач.
План
1. Дослідити чи зустрічаються в живій природі призматичні форми.
2. Представити зображення кристалів деяких хімічних елементів.
3. Хто з великих вчених минулого займався вивченням бджолиних стільників.
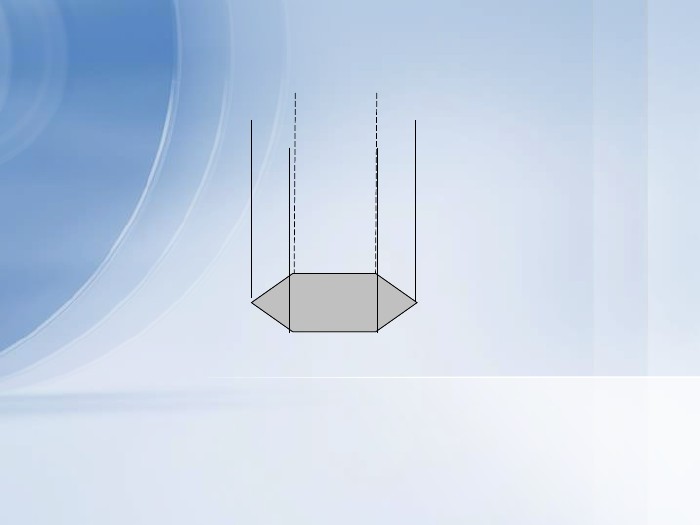
4. Дослідити чому чарунка стільника має форму шестигранної призми
Оцінювання звітів груп
1. Уміння та правильність розв’язування задач.
2. Завершеність,повнота,зрозумілість викладеного матеріалу,оригінальність та різноманітність оформлення,грамотність,новизна.
3. Злагодженість роботи групи,максимальна участь усіх членів у звіті.
Задачі до уроку-проекту
1. У правильній чотирикутній призмі площа основи дорівнює 144 см2,а висота—10см. Знайдіть площу діагонального перерізу.
2. Основою прямої призми є трапеція АВСД,у якої АД=21см,ВС=11см,АВ=СД=13см. Знайдіть площу повної поверхні призми та площу перерізу, який проходить через ребра АД і В1С1,якщо периметр діагонального перерізу дорівнює 58см.
3. Виміри прямокутного паралелепіпеда 3,4,5. Під яким кутом нахилена діагональ паралелепіпеда до площини найменшої його грані?
4.Знайдіть діагоналі прямого паралелепіпеда,якщо вони утворюють з площиною основи кути 30° і 45°, а сторони основи дорівнюють 7см і 17см.
5. Основою призми є правильний трикутник зі стороною a. Одна з бічних граней перпендикулярна до площини основи і є ромбом з гострим кутом α. Знайдіть об’єм призми. Обчисліть, якщо a=17см, α=65°.
6. Прямокутна кімната довжиною 5,6м ,шириною 3м і висотою 2,5м обклеєна шпалерами. В кімнаті є вікно шириною 2,3м і висотою 1,3м та 2 дверей шириною по 1,1 м і 2,1 м. Скільки потрібно мати рулонів шпалер,якщо довжина кожного рулону 10м і ширина 53см?
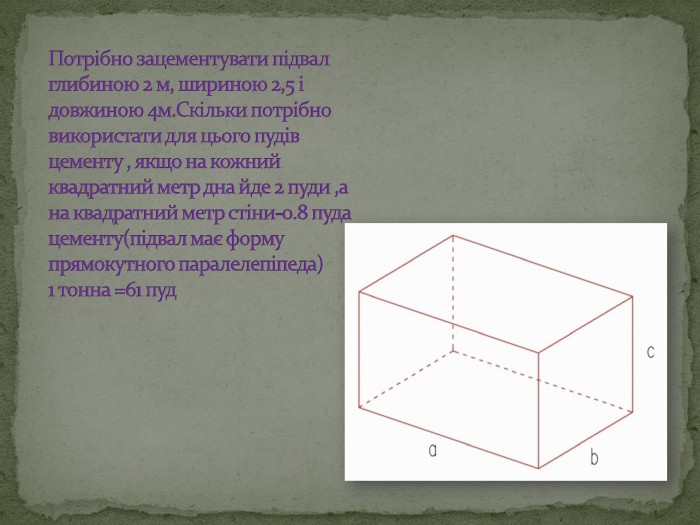
7. Потрібно зацементувати підвал глибиною 2м,шириною 2,5м і довжиною 4м.Скільки потрібно використати для цього пудів цементу,якщо на кожний квадратний метр дна йде 2 пуди,а на квадратний метр стіни-0,8пуда цементу?
8. Двосхилий дах має форму 3-гранної призми;дах простягається уздовж будинку на 21м,ушир- 8,5м,а висота даху – 3,2м.Скільки м займає поверхня даху?
9. Господарська будівля довжиною 17м,шириною 11м, висотою від землі до даху – 496см, зроблена із цегли. У ній знаходяться: 2 дверей висотою по 284см, шириною 195см, 6 вікон шириною по 709см, висотою по 355см.Скільки пішло цегли на стіни стайні, якщо на 1кв.м стіни потрібно 198 штук цеглин?
10. Скільки цеглин потрібно для кладки 18 стовпів висотою 4м з перерізом у вигляді квадрата зі стороною 7дм?Розмір цеглини 1дм х 1,5дм х 3дм.Додати 5% на злам.
11. Для здоров´я учнів необхідно ,щоб у класі на кожного учня припадало не менш ніж 6 м кубічних повітря. Клас довжиною 10м, шириною 6м,висотою 3,5м.Скільки учнів може перебувати в ньому без шкоди для здоров´я?
12. Підлога в прямокутному залі викладена мармуровими плитами. Кожна плита має форму правильної 8-кутної призми зі стороною основи 6,4см і товщиною 2,5 см. Яку площу займає підлога, якщо маса всіх плит 89 690кг?
13. Визначити місткість трикутної шафки у ванній кімнаті, основою шафки є рівнобедрений прямокутний трикутник, рівні сторони якого мають по 50см, а більша (передня) грань займає на 1656,8кв.см більше,ніж кожна бічна грань.
14. Під час сильної зливи за 1год. Випадає шар води висотою 37мм.Визначити масу води, яка випала за такої зливи на прямокутному полі довжиною 100м та шириною 80м, якщо злива тривала 1¼ год. 1 куб.м води має масу 1т.
15. Один із найбільших метеоритів має приблизну форму прямокутного паралелепіпеда 4м завдовжки,2,5м завширшки і 2м у висоту. Його було знайдено в 1894 році поблизу мису Йорк.1 куб.см речовини метеорита має масу 4г.Яку масу має такий метеорит?
16. У мікроскоп розгледіли крупинку кухонної солі кубічної форми з ребром довжиною 0,01мм.1 куб.см кухонної солі має масу 2г.Скільки таких мікроскопічних крупинок повинно піти на 410г?
17. На позолоту 1 кв.м купола витрачається 1г золота. Яка товщина шару позолоти?1 куб. см має масу 20г.
18. Сніжинка у формі правильної 6-гранної призми має діаметр основи 0,14мм, а висоту- 0,34мм (у середньому). Яку масу має мільйон таких сніжинок?1куб.см льоду має масу 0,9г.
18. Чи вистачить у вас сили підняти куб литого золота з ребром 18,8 см?Густина золота 19,3г/см.
19. Переріз залізничного насипу має форму рівнобічної трапеції,висота якої дорівнює 3м, а сторони основ 4м та 8м.Скільки необхідно землі на 1 км насипу?
20. Переріз каналу має вид трапеції. Ширина каналу на рівні води 12,5м, ширина дна 8,5 м, глибина каналу 3м, швидкість течії води 1,6 км/год. Яка кількість води протікає через переріз каналу за 1с?
21.За кожним ударом серце людини виштовхує 175 куб, см крові. Серце робить 75 ударів за хвилину. Яких розмірів кубічну посудину потрібно було б мати, щоб вмістити кількість крові,яку перекачує серце за добу?
Список літератури
- Г.М.Возняк, М.П.Маланюк «Взаємозв´язок теорії з практикою в процесі вивчення математики» Київ «Радянська школа» 1989р.
- Н.А.Терешин «Прикладная направленность школьного курса математики» Москва «Просвещение» 1990 г.
- «Розв´язування прикладних задач геометричного змісту». Автор: А. Овдієнко, газета «Математика»№22 червень 2008 ст. 19, видавництво «Шкільний світ».
- «Математичне моделювання під час розв´язування задач». Автори:Я.Бродський, С.Великодний,О.Глюза, О.Павлов, газета «Математика» №40 жовтень 2005р. ст.6, видавництво « Шкільний світ».
- «Про прикладну спрямованість матеріалу, пов´язаного із вивченням призми». Автор:А.В.Прус, газета «Математика в школах України»№13 2005р.
- «Метод проектів на уроках математики». Упоряд. Л.К. Гладій. Видавництво «Ранок», 2012.
- Газета «Математика в школах України» №27, вересень, 2009р.
- Газета «Математика в школах України» №5, травень, 2013р.
- Газета «Математика в школах України» №15, травень, 2014р.
- Газета «Математика» №3, січень, 2008р.
- «Геометрія 11 клас». Г.П.Бевз, В.Г.Бевз, Н.Г.Владімірова, В.М.Владіміров.


про публікацію авторської розробки
Додати розробку