Урок. «Відношення і пропорції. Відсоткові розрахунки»

Урок з підприємницьким тлом                                                                 «Відношення і пропорції. Відсоткові розрахунки»

    Сокол Лариса Анатоліївна – учитель математики                    кз «Олешківська гімназія» м.Олешки Херсонської обл.

Цільова група:

• учні 6 класу

Тривалість:

• 45 хв.

Мета:

• закріпити в учнів знання з теми «Відношення  і пропорції. Відсоткові розрахунки» ;
• вдосконалити навички обчислення відношень чисел та величин,  інших математичних розрахунків;
• створити умови для усвідомлення цінності практичного використання формули основної властивості пропорції у підприємницькій діяльності;
• розвивати ініціативність, лідерські якості, комунікативні вміння;
• виховувати наполегливість, працьовитість, інтерес до математики, відповідальність.

Операційні цілі (завдання):

Після закінчення уроку учень знає що таке:

• відношення;
• пропорція;
• пряма пропорційна залежність;
•  відсоток;
• відсоткове відношення;

     формулює:

•  означення відношення;
• означення пропорції;
• означення відсоткового відношення;
• основну властивість пропорції;
• означення відсотка;

     розуміє

•  значення математики для ведення успішної підприємницької діяльності;

вміє

•  знаходити відсоток від числа та число за його відсотком;
• розв’язувати задачі економічного змісту;

може

•  аналізувати проблемну ситуацію;
• шукати оптимальні шляхи вирішення проблеми;
• здійснювати градацію цінностей;
• виявляти ініціативу;
• робити висновки;
• співпрацювати в команді.

Методи і техніки:

• «Мікрофон»;
• «Мозковий штурм»;
•  «Незакінчене речення».

Обладнання:

• проектор;
• картки із завданнями самостійної роботи;
• картки для самооцінки роботи в групі.

 

Допоміжні матеріали:

Додаток 1. Домашнє завдання

Додаток 2. Задача для самостійної роботи.

Додаток 3. Інтерактивна вправа “Мікрофон”.

Додаток 4. Усна математична розминка.

Додаток 5. Аркуші з завданнями.

 Додаток 6. Інтерактивна вправа “Мозковий штурм”.

Додаток 7. Математичні розрахунки.

Додаток 8. Завданнями самостійної роботи.

Додаток 9. Зразок розв’язування завдань самостійної роботи.

 

Хід уроку

1. Вступна частина

1.1 Вмотивуйте навчальну діяльність учнів на уроці. Повідомте, що вміння розв’язувати текстові задачі – це показник рівня математичного мислення. Таке вміння необхідне будь якій людині, яка прагне досягти серйозних успіхів в оволодінні сучасних професій.

• 1.2. Повідомте учням тему і мету уроку - зрозуміти причини та сутність проблем з якими їм доведеться зустрітися в недалекому майбутньому і навчитися знаходити різні математичні моделі для вирішення економічних проблем.

1.3. Перевірте виконання домашнього завдання (Додаток 1).

1.4. Запропонуйте учням самостійно розв'язати аналогічну задачу і звірити одержані результати зі зразком (Додаток 2).

1.5. При виявленні помилкових результатів запропонуйте учням пригадати формули знаходження невідомого члена пропорції і здійснити швидку корекцію обчислень.

1.6. Для  актуалізації опорних знань учнів проведіть інтерактивну вправу “Мікрофон” (Додаток 3).

1.7.Для перевірки навиків обчислення запропонуйте усну математичну розминку (Додаток 4).  

2. Основна частина

2.1. Повідомте учнів, що далі вони будуть розв’язувати задачі використовуючи інтерактивну вправу “Мозковий штурм” .

Це ефективний метод колективного обговорення, пошук рішень, що спонукає учасників проявляти свою уяву і творчість в ухваленні рішень, освоєнні теоретичних положень й оволодінні практичними обчислювальними навичками.

2.2. Об’єднайте учнів у 4 групи за допомогою карток чотирьох кольорів і запропонуйте кожній групі зайняти місце за окремим столом. Роздайте аркуші з завданнями (Додаток 5 ).

2.3. Коротко поясніть учням правила цього методу (Додаток 6).                                              2.4. Виділіть на обговорення задач  приблизно 5 хв., а на проведення обчислень 15 хв.

2.5. Після закінчення роботи попросіть представників кожної групи презентувати результати роботи. Важливо, щоб учні розповіли, чи відбувалася зміна рішень під час роботи. Запропонуйте учасникам інших груп проаналізувати представлені способи розв’язувнь та правильність математичних розрахунків (Додаток 7).

2.6. Для контролю знань та умінь виконайте самостійну роботу (Додаток 8).

2.7. Запропонуйте учням здійснити взаємоперевірку (Додаток 9).

3. Підсумкова частина

3.1. Підведіть підсумок уроку через інтерактивну вправу «Незакінчене речення». (Додаток 10).

3.2. Запропонуйте учням провести самооцінювання роботи в групі. Кожне запитання – 0-2 бала за зразком. (Додаток 11).

3.3. На домашнє завдання запропонуйте скласти та розв’язати 3 задачі економічного    змісту та  задачу на використання властивостей обернено пропорційних величин.

 

Додаток 1

Домашнє завдання

• Відношенням називається…(частка від ділення або дріб)
• Відсотковим відношенням називається…( відношення двох чисел виражене у відсотках)
• Пропорцією називається…(рівність двох відношень)
• Основна властивість пропорції…(добуток крайніх членів дорівнює добутку середніх членів)
•  Щоб знайти невідомий середній член пропорції…(досить добуток крайніх членів пропорції поділити на відомий середній член пропорції)
• Щоб знайти невідомий крайній член пропорції…(досить добуток середніх членів пропорції поділити на відомий крайній член пропорції)
• Один відсоток – це…(сота частина числа)
• Як знайти 1% від числа …(поділити його на 100)
• Як знайти число за відомим його 1% …(помножити його на 100)
• Як перетворити відсотки у десятковий дріб …(поділити його на 100)
• Як перетворити десятковий дріб у відсотки …(помножити його на 100)
• Як знайти відсоток від числа …(число помножити на відсоток)
• Як знайти число за його відсотком …(число поділити на відсоток)
• Як знайти відсоткове відношення … (знайти відношення чисел і помножити на 100)

 

Додаток 2.

 Задача для самостійної роботи.

Один гектар лісу поглинає за рік 9,35 т вуглекислого газу і виділяє 8,2 т кисню, який забезпечує дихання 200 людей. Скільки кілограм кисню потрібно на рік для дихання учням 6 класу, в якому навчається 30 учнів? 

Розв’язок:

200 людей – 8,2 т

30 учнів     –  ?

 

Х = = 1230 (кг)

 

Відповідь: 1230 кг.

 

Додаток 3.

 Інтерактивна вправа “Мікрофон”.

Інтерактивна вправа «Мікрофон» дає змогу кожному учневі у визначеному порядку висловити свою думку.

Правила проведення:

1.   Запропонуйте учням проблему.

2.   Дайте уявний «мікрофон» (будь-який предмет).

3.   Кожен учень, узявши його, має висловити власну думку й передати «мікрофон» іншому.

4.   Коли хтось висловлюється, інші не мають права щось говорити.

5.   Відповіді не коментуються й не оцінюються.

 

Додаток 4.

 Усна математична розминка.

• Встановіть відповідність між відсотковим значенням та кількістю учнів школи

                100%       чверть учнів школи

                10%         всі учні школи

                50%         десята частина учнів школи

                25%         половина всіх учнів школи

• Який із дробів дорівнює даному відсотку

 80%        3/4         45%         9/20         15%       1/4          55%      7/10 

                2/3                          3/5                          3/20                     3/5

                4/5                          3/10         1/10           11/20

                7/10                        5/10         7/10                     1/2

• Знайдіть 10% від числа: 140 ; 300 ; 428 ; 6 .    
• Знайдіть число, 50% якого дорівнюють: 7; 20; 65.
• Виразіть у відсотках відношення : 4:10; 5:20; 13:50  

     

Додаток 5.

 Аркуші з завданнями.

Вибір житла

Влітку батьки Петрика вирішили, що восени вони будуть купувати будинок, який коштував 90000 грн, але восени він подорожчав на 15%. Та їм стало відомо, що взимку вартість будинку знизиться на 20%. Батьки звернулись до Петрика за допомогою: - Чи варто їм купувати будинок восени?

Кредит на житло

Батьки почали сперечатися в якому банку взяти кредит. Мама пропонує в банку  «Вибір» під 12% річних на 5 років. А батько стоїть на своєму, що треба брати кредит у банку «Допомога» на 3 роки, під 15% річних. Якому банку вони переплатять менше грошей і на скільки?

Витрати на ремонт

На зекономлені гроші від кредиту батьки вирішили відремонтувати будинок. На фарбу витратити  15% всіє  вартості ремонту, на шпалери – 10%, на меблі – 40%, а решту на побутову техніку. Допоможіть батькам Петрика підрахувати скільки потрібно грошей на фарбу, шпалери, меблі та побутову техніку окремо.

Закупка товару

Торгівельна мережа «Господар» встановила знижки на певні товари. Але в магазині № 4 на : побутову техніку – 5%, меблі – 10%, фарбу – 5%, шпалери – 10%, а в магазині № 9 на : побутову техніку – 8%, меблі – 6%, фарбу – 8%, шпалери – 6%. Батьки Петрика знову звернулись до нього за допомогою: – Де краще їм купувати товари?

 

 Додаток 6.

 Інтерактивна вправа “Мозковий штурм”.

Мозковий штурм — це ефективний метод колективного обговорення, пошук рішень, що спонукає учасників проявляти свою уяву і творчість. Результат досягається шляхом вільного вираження думок усіх учнів і допомагає знаходити кілька рішень з конкретної теми.

Під час «мозкового штурму» учасники дотримуються таких правил:

— намагаються зібрати якомога більше ідей щодо вирішення проблеми, розв’язання завдання;

— не відкидають будь-яку ідею, навіть якщо вона здається фантастичною, нездійсненною або суперечить загальноприйнятій думці;

— подають необмежену кількість ідей або розвивають ідеї інших учасників;

— не обговорюють, не критикують висловлювання, твердження інших, не намагаються давати оцінку запропонованим ідеям на етапі їх висування.

 

Додаток 7.

Математичні розрахунки.

Вибір житла

Влітку батьки Петрика вирішили, що восени вони будуть купувати будинок, який коштував 90000 грн, але восени він подорожчав на 15%. Та їм стало відомо, що взимку вартість будинку знизиться на 20%. Батьки звернулись до Петрика за допомогою: – Чи варто їм купувати будинок восени?

Розв’язок:

І спосіб:

1. 90000 + 0,15 · 90000 = 90000+13500=103500 (грн.) – вартість будинку восени.
2. 103500 – 0,2 · 103500 = 103500 – 20700 = 82800 (грн.) – вартість будинку взимку.

Відповідь: 82800 грн.

 ІІ спосіб:

1. 90000 грн. – 100%

Х        грн. – 15%

Х = сума, на яку подорожчав будинок.

2. 90000 + 13500 = 103500 (грн.) – вартість будинку восени.
3. 103500 грн. – 100%

Х          грн. – 20%

Х = – сума, на яку подешевшав  будинок.

4. 103500 – 20700 = 82800 (грн.) – вартість будинку взимку.

Відповідь: 82800 грн.

 

Кредит на житло

Батьки почали сперечатися в якому банку взяти кредит. Мама пропонує в банку  «Вибір» під 12% річних на 5 років. А батько стоїть на своєму, що треба брати кредит у банку «Довіра» на 3 роки, під 15% річних. Якому банку вони переплатять менше грошей і на скільки?

Розв’язок:

1. 0,12 · 82800 грн. · 5 років = 9936 · 5 = 49680 грн. за 5 років заплатять банку «Вибір»;
2. 0,15 · 82800 грн. · 3 роки = 12420 · 3 = 37260 грн. за 3 роки заплатять банку «Довіра»;
3. 49680 грн. – 37260 = 12420 грн.

Відповідь: Банку «Довіра» вони переплатять менше на 12420 грн.

 

Витрати на ремонт

На зекономлені гроші від кредиту батьки вирішили відремонтувати будинок. На фарбу витратити  15% всіє  вартості ремонту, на шпалери – 10%, на меблі – 40%, а решту на побутову техніку. Допоможіть батькам Петрика підрахувати скільки потрібно грошей на фарбу, шпалери, меблі та побутову техніку окремо.

Розв’язок:

1. 12420 грн. · 0,15 = 1863 грн. – на фарбу;
2. 12420 грн. · 0,1 = 1242 грн. – на шпалери;
3. 12420 грн. · 0,4 = 4968 грн. – на меблі;
4. 100% -  (15% + 10% + 40%) = 35% - на побутову техніку.
5. 12420 грн.·  0,35 = 4347 грн. – на побутову техніку.

Відповідь: на фарбу  – 1863 грн., на шпалери – 1242 грн., на меблі – 4968 грн., на побутову техніку – 4347 грн.

 

Закупка товару

Торгівельна мережа «Господар» встановила знижки на певні товари. Але в магазині № 4 на : побутову техніку – 5%, меблі – 10%, фарбу – 5%, шпалери – 10%, а в магазині № 9 на : побутову техніку – 8%, меблі – 6%, фарбу – 8%, шпалери – 6%. Батьки Петрика знову звернулись до нього за допомогою: – Де краще їм купувати товари?

          Розв’язок:

І спосіб:

4347*0,05 + 4968*0,1 + 1863*0,05 + 1242*0,1 = 217,35 + 496,8 + 93,15 + 124,2 = 931,5(грн.) – знижки в магазині №4.

4347*0,08 + 4968*0,06 + 1863*0,08 + 1242*0,06 = 347,76 + 298,08 + 149,04 + 74,52 = 869,4(грн.) – знижки в магазин №9.

931,5 > 869,4

Відповідь: краще їм купувати товари в магазині №4.

ІІ спосіб:

0,35*0,05 + 0,4*0,1 + 0,15*0,05 + 0,1*0,1 = 0,0175 + 0,04 + 0,0075 + 0,01 = 0,075 – відсоткова знижка в магазині №4.

0,35*0,08 + 0,4*0,06 + 0,15*0,08 + 0,1*0,06 = 0,028 + 0,024 + 0,012+ 0,006 = 0,07 – відсоткова знижка в магазині №9.

 > 1.

Відповідь: краще їм купувати товари в магазині №4.

 

 

Додаток 8.

Завдання самостійної роботи.

І. 1. Площа поля 32 га. Засіяли 80% поля. Скільки гектарів засіяли? 

    2. Площа поля 32 га. Засіяли 25,6 га поля. Скільки відсотків поля ще треба засіяти? 

    3. Число зменшили на 20%. На скільки відсотків необхідно збільшити одержане число, щоб знову дістати задане?

ІІ.1. Маса вершків становить 21% маси молока. Скільки потрібно взяти молока, щоб дістати 84 кг вершків?

    2. Маса вершків становить 21% маси молока. Яку масу знежиреного молока отримаємо з 400 кг цільного?

    3 Число збільшили на 25%. Наскільки відсотків необхідно зменшити одержане число, щоб знову дістати задане?

ІІІ.1.  У 200 г розчину міститься 18 г цукру. Скільки відсотків цукру міститься в розчині?

      2. У 200 г розчину міститься 18 г цукру. Скільки відсотків води міститься в розчині?

      3. Число зменшили на 20%. На скільки відсотків необхідно збільшити одержане число, щоб знову дістати задане?

 ІV.1. У 200 г розчину міститься 18 г цукру. Скільки відсотків цукру міститься в розчині?

       2. У 200 г розчину міститься 18 г цукру. Скільки відсотків води міститься в розчині?

       3. Число збільшили на 25%. Наскільки відсотків необхідно зменшити одержане число, щоб знову дістати задане?

 

Додаток 9.

 Зразок розв’язання завдань самостійної роботи.

1. Завдання середнього рівня:      

*Площа поля 32 га. Засіяли 80% поля. Скільки гектарів засіяли? 

 І спосіб:

1. 80% - 0,8; 
2. 32 · 0,8 = 25,6 га

 ІІ спосіб:

1. 32 га. – 100%

Х га.  – 80%                                                                                                                                                    

Відповідь: 25,6 га.

*Маса вершків становить 21% маси молока. Скільки потрібно взяти молока, щоб дістати 84 кг вершків?

 І спосіб:

1. 21% - 0,21
2. 84 : 0,21 = 400 кг.

  ІІ спосіб:

1. 84 кг – 21%

Х кг  – 100%

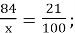2.   х =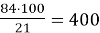

Відповідь: 400 кг.

*У 200 г розчину міститься 18 г цукру. Скільки відсотків цукру міститься в розчині?

 І спосіб:

1. 18:200·100% = 9%.

   ІІ спосіб:

1. 200 г – 100%

  18 г – х%

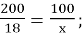2.   х=

Відповідь: 9%

2. Завдання достатнього рівня:

*Площа поля 32 га. Засіяли 25,6 га поля. Скільки відсотків поля ще треба засіяти? 

1.  32 – 25,6 = 6,4 га – потрібно засіяти
2. 6,4:32·100% = 0,2 ·100% = 20%.

Відповідь: 20%

*Маса вершків становить 21% маси молока. Яку масу знежиреного молока отримаємо з 400 кг цільного?

1. 100%  - 21% = 79% - відсоток знежиреного молока
2. 400 · 0,79 = 316 кг.

Відповідь: 316 кг.

*У 200 г розчину міститься 18 г цукру. Скільки відсотків води міститься в розчині?

1. 200 г – 18 г = 182 г – води в розчині.
2. 182 :200 · 100% = 0,91 · 100% 91%

Відповідь: 91%.

3. Завдання високого рівня:

*Число зменшили на 20%. На скільки відсотків необхідно збільшити одержане число, щоб знову дістати задане?

1. Нехай задане число – х
2. х – 0,2х = 0,8х – число зменшене на 20%
3. 0,2х:0,8х = 0,25 – 25%

Відповідь: на 25%

*Число збільшили на 25%. Наскільки відсотків необхідно зменшити одержане число, щоб знову дістати задане?

1. Нехай задане число – х
2. х + 0,25х = 1,25х – число збільшене на 25%
3. 0,2х :1,25х = 0,2 – 20%

Відповідь: на 20%

 

Це спосіб підведення підсумку виконаної роботи. Він дає змогу ґрунтовніше працювати над формою висловлення власних ідей, порівнювати їх з іншими Робота за такою методикою дає присутнім можливість долати стереотипи, вільніше висловлюватися стосовно запропонованих тем, відпрацьовувати вміння говорити стисло, але по суті й переконливо.                                                                                                                       Потрібно визначити тему, з якою учні будуть висловлюватися в колі ідей, сформулювати незакінчене речення і запропонувати учням закінчити його, наприклад:«На сьогоднішньому уроці для мене найважливішим відкриттям було...»; «Ця інформація дає нам підстави для висновку, що...»; «Це рішення було прийнято, бо...» тощо. Кожен наступний учасник обговорення має починати свій виступ із запропонованої формули.

Додаток 11.

Самооцінка роботи в групі

Прізвище, ім’я учня ____________________________________

1. Активна участь у роботі групи ___________________________________________

2. Ваші пропозиції, які врахувала група ___________________________________

3. Підтримка іншим членам групи, заохочення їх до роботи _______________

4. Участь у проведенні обчислень______________________________

5. Узагальнення думки інших і просування роботи групи вперед _______________

6.  Участь у представленні результатів _________________________________________

Всього балів ______________