Урок ”Відношення та пропорції” (6 клас за програмою Росток)

Урок ”Відношення та пропорції” (6 клас за програмою Росток)

Тема: Відношення та пропорції

Мета: Систематизувати та узагальнити знання учнів по даній темі, вміння та навички розв’язання рівнянь з використанням основної властивості пропорції, розрізняти прямо пропорційні та обернено пропорційні величини та з їх допомогою розв’язувати задачі, вміння розв’язувати задачі на пропорційний поділ.

Розвивати логічне мислення, культуру мовлення, швидкість реакції, вміння застосовувати набуті навички до розв’язання життєвих задач.

Хід уроку

І. Організаційний момент.

Вітаюсь, перевіряю готовність учнів до уроку.

На сьогоднішньому уроці ми з вами повинні систематизувати та узагальнити матеріал даної теми на прикладах різних задач практичного змісту, оскільки пропорції мають широке застосування в хімії, фізиці, в кулінарії та повсякденному житті. В побуті більшість життєвих задач ваші бабусі і дідусі розв’язують з допомогою пропорцій.

ІІ. Перевірка домашнього завдання.

№293

5.4 кг – 2.5 хв

Х кг – 60 хв

(кг)

Відповідь: 129.6 кг картоплі

№294 (2)

а₁:а₂:а₃=0.2:0.4:0.6=2:4:6=1:2:3

1х+2х+3х=9.6

6х=9.6

Х=1.6

а₁=1.6

а₂=1.6·2=3.2

а₃=3·1.6=4.8

Відповідь: 9.6=1.6+3.2+4.8

№296

Р_Δ=68 см; a:b:c=4:5:8

Нехай х см – 1 частина, тоді a=4х; b=5х; c=8х.

4х+5х+8х=68

17х=68

Х=68:17

Х=4

1) a=4·4=16 (см);

2) b=5·4=20 (см);

3) c=4·8=32 (см);

с-а=32-16=16 (см).

Відповідь: різниця найбільшої та найменшої сторони 16 см.

ІІІ. Актуалізація опорних знань.

Усні вправи:

1) Що називається пропорцією?

2) Основна властивість пропорції?

3) Навести приклад пропорції?

4) Які величини називають прямо пропорційними?

5) Які величини називають обернено пропорційними?

6) Якими будуть величини:

А) час виконання даного об’єму роботи і продуктивність праці;

Б) відстань по залізниці і вартість квитка.

7) Назвати формулу оберненої пропорційності та прямої пропорційності.

8) Як називається число k?

9) Чому дорівнює k для прямо пропорційних величин і для обернено пропорційних величин.

10) Серед формул назвати пряму пропорційність та обернену пропорційність:

а) S=7a

б)

в) k=8:x

г) a·b=10

д) a=b+3

е)

є) A=0.5t

ж) d=3m²

11) Спростити відношення:

А) 0.3:0.4:0.5;

Б) 27:18:24;

В)

12) Задача:

Для приготування вишневого варення беруть 2 частини цукру та 3 частини ягід. Скільки кілограм цукру і скільки кілограм ягід треба взяти, щоб отримати 10 кг варення, якщо відомо, що під час приготування його маса зменшується в 1.5 разів.

1) 10·1.5=15 (кг)

2) 2х+3х=15

5х=15

Х=3

Відповідь: 6 кг цукру і 9 кг ягід.

IV. Формування вмінь та навичок.

Розв’язування завдань з коментарями біля дошки.

Сильні учні, що працюють самостійно та дають задачу на перевірку вчителю, одержують оцінки.

№280

1) 5600·0.1=560 (монет) на благодійність;

2) 5600·0.35=196 (монет) склали податки;

3) 5600-(560+1960)=3080 (монет).

а₁:а₂=2:5;

а₁:а₂=12:30;

а₂:а₃=6:7;

а₂:а₃=30:35, отже

а₁:а₂:а₃=12:30:35

нехай х монет складає 1 частину, тоді 12х+30х+35х=3080

77х=3080

Х=40

1) 12·40=480 (монет) одержить І шукач;

2) 30·40=1200 (монет) одержить ІІ шукач;

3) 40·35=1400 (монет) одержить ІІІ шукач.

Відповідь: 480 монет, 1200 монет, 1400 монет.

Задача 1:

В оцтовій есенції міститься  80% оцтової кислоти, концентрація столового оцту – 9% оцтової кислоти. В господині є рецепт на приготування консервованих огірків в якому використовується  столовий оцет. Скільки води їй потрібно додати до 180 г есенції, щоб отримати столовий оцет.

Учень біля дошки виконує задачу за допомогою пропорцій, учні за партами стараються виконати задачу двома способами – способом пропорцій та по дія, знаходячи дріб від числа та число за даним значенням дробу.

Один з учнів коментує виконання задачі другим способом, вчитель швидко записує її на дошці, діти перевіряють правильність розв’язку та отримують однакові відповіді, розв’язуючи задачу різними способами.

І спосіб:

1) 180 г есенції – 100%

 Х г есенції – 80%

(г) оцтової кислоти в есенції

2) х г розчину – 100%

144 г кислоти – 9%

(г) розчину оцту

3) 1600-180=1420 (г) води

Відповідь: потрібно додати 1420 г води.

ІІ спосіб:

1) 180·0.8=144 (г) оцтової кислоти в есенції

2) 144:0.09=1600 (г) розчину оцту

3) 1600-180=1420 (г) води

Самостійна робота.

На 2 варіанти у вигляді гри – “Хто  швидше?”

2 учні виконують завдання за дошкою, інші – працюють самостійно в зошитах. (7-10) учнів, які першими впорались з завданнями отримують оцінки.

І-варіант

№270 (4)

Розв’яжемо рівняння методом терезів, віднімаючи від обох частин рівняння 4х, одержимо:

Х=2·7

Х=14

Відповідь: х=14

ІІ-варіант

№273 (3)

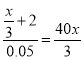
Х+6=2х

Розв’яжемо рівняння методом терезів, віднімаючи від обох частин рівняння х, одержимо:

Х=6

Відповідь: х=6.

Задача №291 (для обох варіантів)

1) 100 г жиру – 10 штук

Х г жиру – 28 штук

(г) жиру

2) 400 г кабачків – 10 штук

Х г кабачків – 28 штук

(г) кабачків

Відповідь: 280 г жиру, 1120 г кабачків.

Для тих хто справився швидше можна запропонувати: І варіант - №281 (2), ІІ варіант – 271 (1).

V. Підсумок уроку.

Діти перевіряють правильність розв’язку, звіряючись із завданнями, що виконали учні за дошкою. Діти підводять підсумок уроку: вказуючи на те, що даний матеріал має широке застосування в побуті, зокрема в кулінарії.

Вчитель виставляє оцінки.

VI. Домашнє завдання.

№295, № 293 (2, 3), (№258 (4) за бажанням дітей).