Урок "Відстані у просторі"

Про матеріал

Конспект уроку з геометрії на тему "Відстані у просторі" (нестандартний урок)

Перегляд файлу

Нестандартний урок

Геометрія. 10 клас

Підготувала:

вчитель математики

Осичнюк І.В.

Тема. Відстані у просторі

Мета: сформувати в учнів поняття відстані у просторі; навчити знаходити відстані у просторі на просторових моделях; «читати» геометричні рисунки; повторити матеріал про відстані на площині; розвивати в учнів логічне мислення; формувати вміння аналізувати, обґрунтовувати відповідь, правильно і лаконічно висловлювати міркування, вміння працювати в групах; виховувати толерантність, ціннісне ставлення до праці.

Обладнання: каркасні моделі просторових фігур, моделі прямих, картки «Відстані у просторі», прості олівці, креслярські інструменти, рисунки до задач, картки з варіантами відповідей до технології «Мозкова атака».

Тип уроку: засвоєння нових знань, умінь та навичок.

Девіз уроку: Серед рівних розумом, за однакових інших умов, переважає той, хто знає геометрію.

Блез Паскаль

ХІД УРОКУ

І. Ознайомлення з темою, метою уроку і девізом

Які завдання ставить перед вами девіз уроку?

II. Вивчення нового матеріалу

1. Прийом «Мозкова атака»

1.1. Запитання до класу:

— Що ви знаєте про відстані на площині?

— Які асоціації у вас викликає тема «Відстані у просторі»?

(Учні відповідають. На дошці вивішуються заготовлені можливі відповіді учнів, а також коротко записується те, що не передбачено вчителем. Приймаються всі відповіді.)

1.2. Пропозиції учнів щодо визначення теми уроку. Що, на їх думку, стосується до теми «Відстані на площині», а що теми «Відстані у просторі».

Читання з помітками
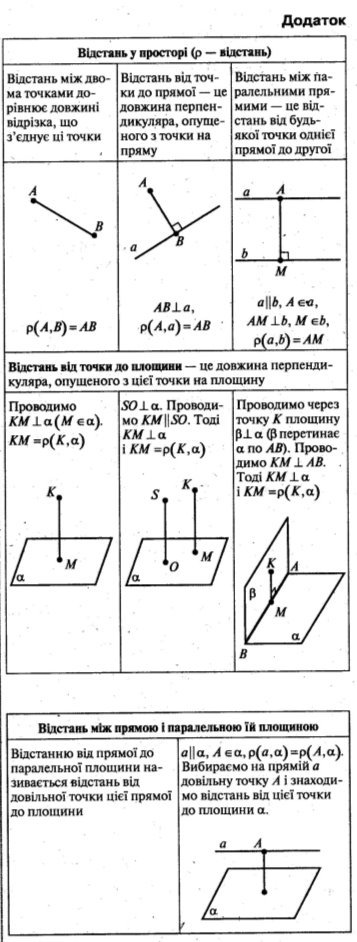
1. А тепер дізнаємось, що насправді стосується теми «Відстані у просторі». Кожен з вас повинен опрацювати текст «Відстані у просторі». На полях олівцем поставте позначку (+), якщо це ви добре знаєте; позначку (—), якщо знали, але забули, позначкою (?) позначаєте новий для себе матеріал. Час обмежений (5 хв). (Додаток)
2. Запитання до класу по закінченні роботи:

Що з матеріалу, з яким ознайомились, вам було відомо?
Що було відомо, але забулось?
Що дізналися нового?
Чи все зрозуміло з прочитаного?
Які висновки зробили для себе?
1. Робота в групах

Клас довільно об'єднуємо в групи. Кожна група отримує каркасну модель призми та моделі прямих. Завдання: на цій моделі знайти всі відстані, які щойно вивчили, користуючись карткою «Відстані у просторі». Учні відповідають чітко, допомагають один одному. Вчитель підходить до кожної групи і ставить завдання знайти ту чи іншу відстань.

Прийом «Закінчити речення» (усно)

Відстань між двома точками — це...
Відстань між точки до прямої — це...
Відстань між паралельними прямими – це...
Відстань між прямою і паралельною їй площиною — це...
Відстань між паралельними площинами — це...
Відстань між мимобіжними прямими — це...
Скільки існує способів знаходження відстані між мимобіжними прямими? (3)

III. Формування вмінь та навичок

5. Розв'язування задач за готовими рисунками (усно)

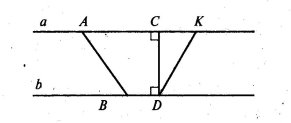$C:\Documents and Settings\Admin\Рабочий стол\Изображение 2 200.jpg$ 5.1. Який з відрізків АВ, СD чи КD є відстанню між паралельними прямими а і b? Чому?

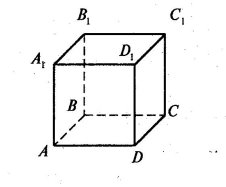$C:\Documents and Settings\Admin\Рабочий стол\Изображение 2 201.jpg$ 5.2. Ребро куба АВСDА₁В₁С₁D₁ дорівнює a. Знайдіть відстань між прямими:

а) АВ і СС₁; б) СС₁ і B₁D₁; в) АС і В₁D₁.

Розв'язання. (На дошці заздалегідь виконано три рисунки куба. Під час усного розв'язування задачі учні кольоровою крейдою наводять відрізок, що дорівнює шуканій відстані.)

а) Спільний перпендикуляр —ребро DС. ВС = а.

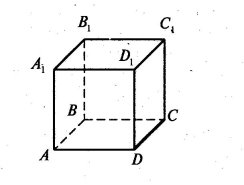
$C:\Documents and Settings\Admin\Рабочий стол\Изображение 2 202.jpg$

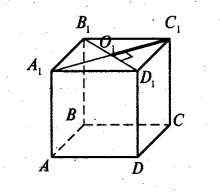$C:\Documents and Settings\Admin\Рабочий стол\Изображение 2 203.jpg$ б) Проведемо діагональ С₁А₁. Спільний перпендикуляр — це відрізок С₁ О.

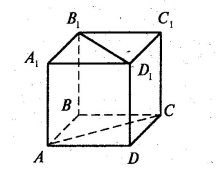$C:\Documents and Settings\Admin\Рабочий стол\Изображение 2 204.jpg$ в) Розглянемо паралельні площини (АВСD) і (А₁В₁С₁D₁), де лежать дані прямі. Їх спільний перпендикуляр, наприклад, ребро АА₁. АА_І = а

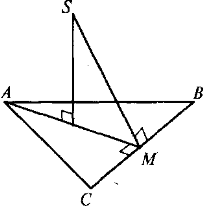
5.3. Який з відрізків є відстанню:

а) від точки S до площини трикутника АВС;

б) від точки S до сторони трикутника?

6. Розв'язування задач (письмово)

Із точки А до площини α проведено дві похилі. Знайдіть відстань від точки А до площини α, якщо похилі мають рівні довжини, що дорівнюють 3 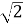см, кут між ними дорівнює 60°, а кут між їхніми проекціями — прямий.

Дано: площина α, т. А α. АО ┴ α, А

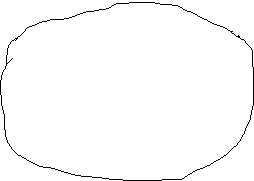АС = АВ = 3√2 см, < САВ = 60⁰,

< АОВ = 90⁰.

Знайти: ρ (А, α) = АО. α

Розв’язання.

Розглянемо АВС: АС = АВ = 3√2 см, В О С

< САВ = 60⁰. Звідси, АВС – рівнобедрений і рівносторонній (<А = <В = <С = 60⁰, АВ = АС = ВС = 3√2 см). АО – є медіаною, бісектрисою і висотою.

Так як проекції рівних похилих рівні, то ВО = СО = = см.

Розглянемо АОС (за умовою <О = 90⁰): АС = 3√2 см, СО = см,

< С = 60⁰. За теоремою Піфагора знайдемо АО:

АО = = = = = 3 см.

Відповідь: АО = 3 см.

Відрізок КА — перпендикуляр до площини правильного трикутника АВС. Знайдіть відстань між прямими ВС і КА, якщо периметр трикутника дорівнює 24 см. К

А В

Дано: КА ┴ (АВС), АВС – правильний (АВ = АС = ВС, = 60⁰ ). Р АВС = 24 см.

Знайти: ρ (ВС, КА).

Розв’язання. Розглянемо АВС: АВ = АС = ВС = = = 8 см.

Проведемо з вершини А на сторону ВС висоту АS, яка є медіаною і бісектрисою. ВS = СS =

За теоремою про три перпендикуляри: АS ┴ ВС, КS ┴ ВС.

Знайдемо відстань між прямими ВС і КА: ρ (ВС, КА) = АS, бо КА ┴ АS і ВС ┴ AS (відстанню між мимобіжними прямими є довжина їх спільного перепендикуляра).

З АСS(< S = 90⁰): tg 60⁰ = , AS = BS · tg 60⁰.

AS = 4 см.

Відповідь: ρ (ВС, КА) = АS = 4 см.

Точка, що віддалена від площини квадрата на 8 см, рівновіддалена від його сторін. Площа квадрата дорівнює 144 см². Знайдіть відстань від точки до сторін квадрата. S