Урок "Використання програмного забезпечення LABWE на уроках алгебри"

ВИКОРИСТАННЯ ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ

LABWE INTERACTIVE WHITEBOARD НА УРОКАХ АЛГЕБРИ

  В статті наводяться приклади використання програмного забезпечення Labwe Interactive Whiteboard на уроках алгебри при вивченні тем функції в різних класах в рамках STEM-освіти та переваги таких занять від традиційних уроків.

   В STEM-освіті часто використовується прийом -  спочатку  дослідження, а вже потім – опанування теорії і нових знань. Це вимагає від учнів  здібностей критично мислити, вміння працювати як в команді так і самостійно, сприяє осмисленню й пошуку причинно-наслідкових зв’язків, розвитку логічного мислення, комунікативних здібностей.

    Використання ІКТ на уроках математики є основою сучасних нестандартних уроків. Не кожен урок математики можна провести як нестандартний, а от використовувати окремі методи сучасних інноваційних технологій вчителі математики  можуть на кожному уроці, що в сучасних умовах - можливо. Це сприяє  продуктивності навчального процесу, створенню необхідних умов для успішного та якісного навчання учнів математики.

   Розглянемо кілька прикладів використання програмного забезпечення Labwe Interactive Whiteboard на уроках алгебри при вивченні  функції. В основному цей прийом використовується як самостійне підведення учнів до засвоєння нових понять і властивостей на початку вивчення теми уроку чи кількох уроків або як можливість узагальнити вивчене. В цьому прийде на допомогу даний програмний засіб. Це зекономить час і дасть можливість цілісно побачити і усвідомити результат теми. Учителю лише потрібно правильно поставити запитання, щоб учні змогли самостійно робили  висновки.

   Алгебра 7 клас

 «Лінійна функція та її графік»

  На етапі вивчення окремих випадків лінійних функцій та їх графіків використовуємо Labwe Interactive Whiteboard. На екрані з’являються графіки лінійних функцій групами, в яких функції об’єднані спільною властивістю. Учням потрібноспівставити та зробити висновки про залежність між формулою функції, її коефіцієнтами та положенням графіка на координатній площині.

І група формул

y = x    y = 2x     y = 0,3x     y = -x    y = -4x     y = -0,25x

(Учні звертають увагу на знак і значення (в порівнянні з 1) коефіцієнта k  та положенням графіка в залежності від цього коефіцієнта)

II група формул

y = x     y = x+3    y = x – 5    y = -x    y = -x + 6     y = -x – 2

(Учні звертають увагу на знак і значення коефіцієнта b  та положенням графіка в залежності від цього коефіцієнта)

III група формул

y = 2x     y = 2x+3    y = 2x – 5    y = -0,3x    y = -0,3x + 6     y = -0,3x – 2

(Учні звертають увагу на знак і значення (в порівнянні з 1) коефіцієнта k  та коефіцієнта b  із положенням графіка в залежності від обох коефіцієнтів)

 Учням пропонується зробити порівняння:

• Що спільного і що відмінного у положенні графіків функцій кожної групи окремо. Який зв'язок між положенням графіка і коефіцієнтами у формулі.

   Після цього варто на закріплення провести графічний диктант, де учні будують ескізи графіків лінійних функцій, а потім перевіряють правильність своїх припущень побудовою за координатами точок.

    Такий підхід до вивчення теми дає можливість показати учням в цілому поняття графіка функції та навчитись встановлювати зв'язок між формулою (коефіцієнтами) та положенням графіка в системі координат. А це в свою чергу дає можливість проконтролювати учневі себе у вірності виконання завдань в темах, пов’язаних з графіками (розв’язування рівнянь графічним способом; знаходження площ фігур за допомогою інтеграла, розв’язування систем рівнянь графічним способом …).

   Алгебра 7 клас

 «Графічний спосіб розв’язування систем лінійних рівнянь»

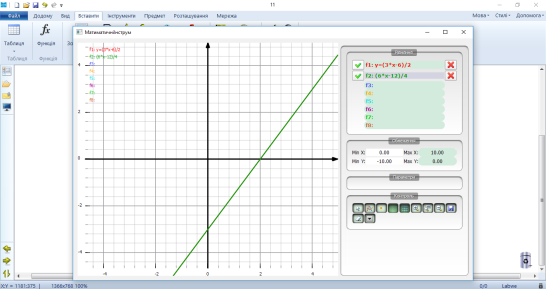
Після того, як учні познайомились із графічним способом розв’язування систем рівнянь для того, щоб вони побачили зв’язок між коефіцієнтами і кількістю розв’язків системи рівнянь.  можна використати також Labwe Interactive Whiteboard. На екрані появляються графічні зображення систем, а учні  спостерігають і роблять висновки про зв’язок відношення коефіцієнтів в системах і кількістю розв’язків.

  2)     

2.    3)  

Учні роблять висновки про зв’язок між коефіцієнтами в системі та кількістю розв’язків системи:

• Якщо всі відповідні коефіцієнти не пропорційні, то система має один розв’язок.
• Якщо всі відповідні коефіцієнти пропорційні, то система має безліч розв’язків.
• Якщо пропорційні лише відповідні коефіцієнти біля змінних, то система не має розв’язків.

  Після цього варто дати самостійну роботу, яка складатиметься з двох етапів: 1) передбачення кількості розв’язків системи;

2) перевірка вірності передбачення  розв’язанням  даних систем графічно.

10 клас Математика (Рівень стандарту)

Степенева функція і її властивості

Формувати поняття степеневої функції, її властивостей, та загального вигляду степеневої функції.  На початку уроку учні пригадують основні степеневі функції вивчені в попередніх класах із степенями 2; 3; -1; 1\2 та їх графіки. Пригадують основні властивості функцій, та як їх можна охарактеризувати за графіком.

Після чого учням пропонується заповнити таблицю властивостей та графіків степеневих функцій за готовими графіками виконаними в програмі Labwe Interactive Whiteboard.

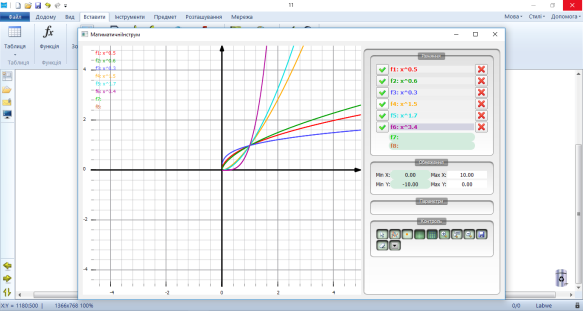
Заповнити таблицю

   10 клас Математика (Рівень стандарту)

Перетворення графіків тригонометричних функцій

на прикладах функцій

Після вивчення теми графіків тригонометричних функцій учням пропонується пригадати перетворення графіків вивчених раніше функцій та спів ставити чи виконуються ці правила для тригонометричних функцій. За готовими графіками учні характеризують властивості тригонометричних функцій  та співставляють зміну властивостей від змін у формулі.

1. y = sinx  y = 2sinx   y = 0.5sinx    y = sin2x   y = sin 0.5x   y = 5sin0.5x

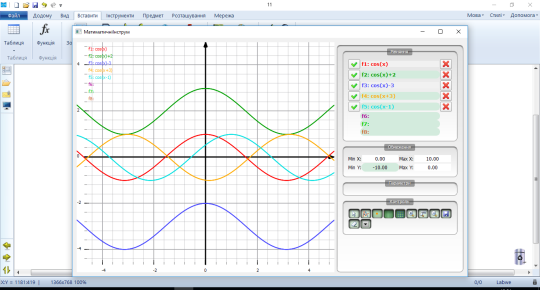2. y = cosx   y = cosx +2   y = cosx - 3   y = cos(x+3)  y = cos(x-1)