Тренажер "ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ"
Вправи-тренажери для відпрацювання навичок диференціювання різних функцій. Матеріал містить групи однотипних завдань на застосування певної формули, правила чи властивості. Призначений для використання як на уроках, так і для самостійної роботи учнів. Завдання можна використовувати для складання багатоваріантних самостійних чи контрольних робіт.
ПРАВИЛА ДИФЕРЕНЦІЮВАННЯ
Вправи-тренажери
Знайдіть похідні функцій:
3.1. y = x9; y = x21; y = x; y = x‒7; y = x‒10; y = x‒1,6; y = x0,8; y = x‒0,3
3.2.
; y 
; y 
;
y 
; y 
3.3.
3.4.
; y 
; y 
; y 
3.5.
2.1. y = 2x 3 + 3x4 + 7; y = 7x2 ‒ 5x8 + 4; y 
+ 5;
y 
2.2.
; y 
; y 
; y 
2.3.
; y 
; y 
2.4.
; y 
3.1. y = (4𝑥 + 1)3; y = (9𝑥 − 3)4; y = (3 + 7𝑥)2; y = (6 + 𝑥)4; y = (4 − 2𝑥)5; y = (7 + 𝑥)5; y = (4 − 𝑥)2; y = (4𝑥 + 3)5; y = (2𝑥 + 1)7; y = (5 + 2𝑥)3; y = (6 − 3𝑥)4; y = (6 − 𝑥)5
3.2. y = (0,5𝑥 + 6)4; y 
; y 
; y 
;
y 
; y 
; y 
; y 
3.3.
; y 
; y 
; y 
4.1. y = (𝑥 − 2)9(x + 2)2; y = (x + 2)6(9 ‒ 3x)4; y = (2x ‒ 3)3; y = (4x ‒ 6)0,5(3 ‒ 2x)0,4; y = (6 ‒ 10x)0,2(5x + 1)5
4.2.
; y 
4.3.
; y 
5.1.
; y 
; y 
; y 
; y 
5.2.
; y 
; y 
; y 
5.3.
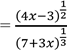; y 
; y 
6.1. y = sin(10𝑥 + 3); y = sin(4𝑥 − 8); y = sin(5 + 4𝑥); y = sin(6 − 2𝑥); y = 5sin(4 + 2𝑥); y = ‒sin(3 + 7𝑥); y = ‒3sin(10 − 𝑥)
6.2. y = cos(5𝑥 + 2); y = cos(7𝑥 − 4); y = cos(9 + 4𝑥); y = cos(3 − 𝑥); y = 4cos(3 + 𝑥); y = ‒cos(−7𝑥 + 3); y = ‒2cos(−9𝑥 + 5)
про публікацію авторської розробки
Додати розробку