Урок: Висота, бісектриса та медіана трикутника

Тема уроку:

Висота, бісектриса та медіана трикутника

Урок геометрії у 7 класі з використанням інтерактивних технологій

Учителя математики

НВК №2 м. Немирова

Капітули Оксани Григорівни

Тема: Висота, бісектриса та медіана трикутника

Мета: сформувати  поняття бісектриси, медіани, висоти трикутника; формувати вміння будувати їх за допомогою лінійки, транспортира і кутника та розпізнавати за готовими малюнками;  розвивати вміння виділяти головне в досліджуваному матеріалі; сприяти розвитку логічного мислення, уваги учнів; виховувати зацікавленість у пізнанні нового, спостережливість, старанність; розуміння та вміння слухати товаришів.

Обладнання: лінійка, транспортир, кутник, роздатковий матеріал, різнокольорові картки.

                                                 ХІД УРОКУ

І. Актуалізація опорних знань.

1. Усне опитування.

1) Який трикутник називають рівнобедреним? Які його сторони називають бічними, а яку – основою?

2) Якими є кути при основі рівнобедреного трикутника?

3) Який трикутник називають рівностороннім?

4) Якими є кути рівностороннього трикутника?

5) Яким є трикутник, у якого два кути рівні?

6) Яким є трикутник, у якого три кути рівні?

2. Усне розв’язування задач за готовими малюнками.

Довести, що на кожному з малюнків трикутник АВС – рівнобедрений.

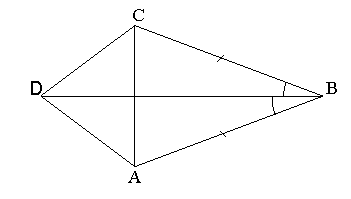
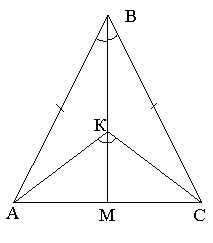
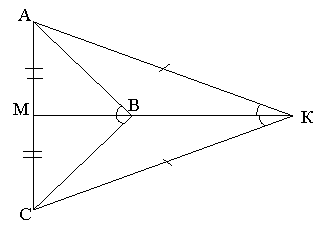
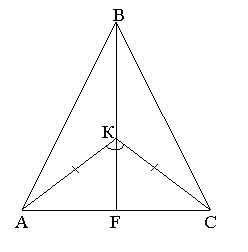
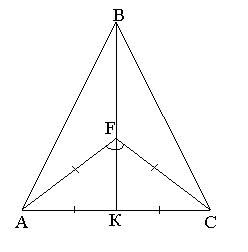
ІІ. Оголошення теми і мети уроку.

ІІІ. Вивчення нового матеріалу.

Технологія «Ажурна пилка».

На попередньому уроці я кожному учневі роздала одну з карток трьох кольорів із записаними номерами на них (від 1 до 3) та сформувала 3 групи, що отримали такі завдання:

1.                      «червоні» - сформулювати означення медіани трикутника, її властивість та побудувати всі медіани трикутника;
2.                      «сині» - сформулювати означення бісектриси трикутника, її властивість та побудувати всі бісектриси трикутника;
3.                      «зелені» - сформулювати означення висоти трикутника, її властивість та побудувати всі висоти трикутника.

Перший етап

Учням пропонується об’єднатися в групи за кольором карток, які вони отримали на попередньому уроці («домашні» групи). Працюючи в таких групах, учні обмінюються інформацією, проводять взаємоопитування, коментують розв’язування домашніх завдань.

Другий етап

Я  пропоную учням об’єднатися в групи відповідно до номерів, записаних на картках («експертні» групи). У кожній «експертній»  групі є представники від кожної «домашньої» групи. Члени груп формулюють означення, властивості тощо, з якими вони ознайомилися вдома та обговорювали в «домашніх» групах. У зошитах роблять відповідні записи.

Інформація від «червоних»

Відрізок, який сполучає вершину трикутника із серединою протилежної сторони, називають медіаною. ВМ – медіана трикутника АВС, бо АМ=МС.

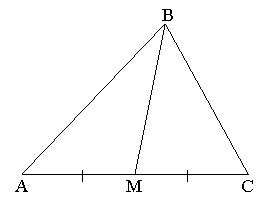
У трикутнику можна побудувати три медіани, які перетинаються в одній точці.

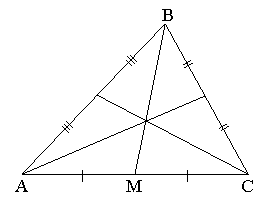
Інформація від «синіх»

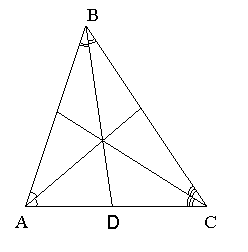
Бісектрисою трикутника називають відрізок бісектриси кута трикутника, який сполучає вершину трикутника з точкою перетину її з протилежною стороною. BD – бісектриса трикутника АВС.

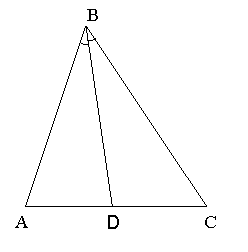
У трикутнику можна побудувати три бісектриси, які перетинаються в одній точці.

Інформація від «зелених»

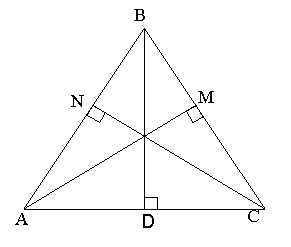
Висотою трикутника, опущеною з даної вершини, називають перпендикуляр, проведений з цієї вершини до прямої, що містить протилежну сторону трикутника. BD, B₁D₁  - висоти трикутників АВС та А₁В₁С₁.

У трикутнику можна побудувати три висоти. Висоти або їх продовження перетинаються в одній точці.

                                             Третій етап

Клас об’єднується в загальне коло для підбиття підсумків. Учні по черзі дають відповіді на запитання вчителя:

1.         Що нового дізналися на уроці?
2.         Що називають медіаною трикутника?
3.         Сформулюйте властивість медіани.
4.         Що називають бісектрисою трикутника?
5.         Сформулюйте властивість бісектриси.
6.         Що називають висотою трикутника?
7.         Сформулюйте властивість висоти.
8.         Скільки медіан, висот і бісектрис можна побудувати в трикутнику?

IV. Застосування набутих знань, умінь і навичок.

Задача 1. Побудуйте в довільному трикутнику АВС медіани та бісектриси. Зробіть висновок про розміщення медіан і бісектрис трикутника.

Задача 2. Побудуйте в трикутнику АВС висоти. Розгляньте два випадки:

 трикутник АВС – гострокутний;

 трикутник АВС – тупокутний.

Зробіть висновок про розміщення висот трикутника.

Задача 3. Побудуйте різносторонній трикутник АВС так, щоб кут В був тупий. За допомогою лінійки, транспортира і кутника побудуйте медіану ВМ, бісектрису BL,  висоту ВН. Порівняйте довжини відрізків ВМ, BL і ВН.

Задача 4. Дано трикутник MNP, PF – його медіана, NF = 10см. Знайдіть MN.

Задача 5. Дано трикутник АВС, СD – його бісектриса, <ACD=54⁰  Знайдіть кут АСВ.

V. Підбиття підсумків, оцінювання учнів.

VІ. Домашнє завдання