Урок з алгебри "Арифметична прогресія та її застосування. Розв'язування прикладних задач"

Урок з алгебри в 9 класi

Тема уроку: АРИФМЕТИЧНА ПРОГРЕСІЯ ТА її ЗАСТОСУВАННЯ. РОЗВ'ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ.

Навчальна мета уроку: узагальнити, систематизувати і розширити знання,
уміння і навички учнів при розв'язуваннi задач по темі: "Арифметична прогресія". Побачити тісний зв'язок між математикою та навколишнім світом.

 

Розвиваюча мета: розвивати прийоми розумової дiяльностi (узагальнення, аналіз,синтез, порівняння); вміння аналізувати та зрозуміло висловлювати власну думку; вміння самостійно здобувати знання, використовуючи різні джерела, логічне мислення, кругозір, увагу, пам'ять, творчі здібності учнів, інтерес до вивчення математики, літератури, біології, фізики.
 

Виховна мета: вміння працювати у групах, взаємовiдповiдальнiсть, прагнення долати труднощі, старанність, математичну культуру мовлення і письма.

Тип уроку: урок закрiплення матеріалу.

Обладнання на уроці: комп'ютер, мультимедійна дошка, таблиця для рефлексії.

Епіграф уроку: «Немає жодної галузі математики, якою б абстрактною вона не була, котра коли-небудь не виявиться застосовною до явищ дiйсного світу»

М.І.Лобачевський

Структура уроку:

I. Підготовчий етап (виявлення цілей уроку й орієнтація учнів у навчальній

діяльності на уроці).(2 хв.)

II.   Актуалізація знань учнів.(до 10 хв)

III.  Вiдпрацьовування умінь і навичок по темі «Арифметична прогресія».

Тестова робота. (10 хв)

VI.  Розв'язок задач практичного напрямку.( до 20 хв)

V.   Підведення підсумків уроку й домашнє завдання.(3 хв)
 

 

 

 

 

 

ХІД УРОКУ

І.Організаційний. момент.
 

Усне вiтання. Перевірити готовність учнів до уроку.
 

Тема сьогоднішнього уроку: «Арифметична прогресія і її застосування». Придивіться уважно: у слові "прогресія" я підкреслила слово, прогрес", що в перекладі з латинської означає "крок вперед". Отже, сама тема нас спонукає зробити крок уперед, досягти прогресу. Для досягнення успіху, нам потрібно сформулювати мету. Я сформулюю її з точки зору нашої спільної навчальної діяльності:

Навчатися застосовувати формули арифметичної прогресії для розв’зування прикладних задач. Ми з’ясували, чого хочемо досягти, але не менш важливим є питання: навіщо це нам потрібно, навіщо вивчається ця тема? Прогресії є відображення світу, що нас оточує. Застосовується прогресія в таких науках, як:

• фізика: під час вивчення тіл, що вільно падають чи рухаються рівноприскорено, під час вивчення процесу радіактивного розпаду;
• економіка та банківська справа: під час виплати відсотків та надання кредитів;
• техніка: під час виготовлення обладнання.

Отже, ми розуміємо актуальність того, над чим працюємо: для виконання завдань ДПА, домашніх завдань, тематичного оцінювання, тощо. Сьогодні на уроці ми закріпимо ваші знання з вивченої теми. Результати вашої роботи перш за все будуть залежати від настрою на цей урок. Нехай він пройде під девізом:

Переконай себе в тому, що арифметична прогресія засвоєна!

 

Оскільки ця тема вивчається не перший урок, звернемось до нашого досвіду, відтворимо знання про арифметичну прогресію та її основні формули, щоб скористатися ними в подальшій роботі.

 

II. Актуалізація знань учнів.

 

Математичний диктант

1. запишіть визначення арифметичної прогресії за допомогою формули;
2. запишіть формулу різниці арифметичної прогресії;
3. запишіть формулу n-го члена арифметичної прогресії;
4. запишіть характеристичну властивість арифметичної прогресії;
5. запишіть формулу суми n перших членів арифметичної прогресії;
6. з даних послідовностей оберіть ті, які є арифметичною прогресією:

а) -1; 3; 7; 11… б) -2; 2; -2; 2… в) -1; 3; -7; 11… д) 3;0; -3; -6…

А тепер перевіримо! Учні виконують взаємоперевірку в парах.

 

 

	Арифметична прогресія
Визначення
Різниця арифметичної прогресії
Формула n-го члена
Характеристична властивість
Формула суми n членів
Арифметичні прогресії	а, в, д

 

III. Тестова робота. Наступним етапом закріплення арифметичної прогресії будуть тести, завдання отримує кожна група, у кожної групи своє завдання.

 

Група 1

 

1. (a_n) – арифметична прогресія 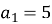 , , 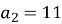d = ?

1. -6   b) 16   c) 6   d) 55

2. Дано арифметичну прогресію 0; -4; …;

Знайти

1. -8  b) 8   c) 4   d) -4

3. Дано арифметичну прогресію, , .

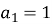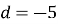Знайти

1. -4   b) -44  c) 44  d) -6

Група 2

1. Дано арифметичну прогресію  , ,

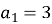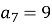Знайти

а) 27   b) 12  c) -42  d) 42

2. Дано арифметичну прогресію ,

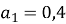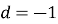
Знайти

1. -8  b) -7   c) 8   d) 7

4. (a_n) – арифметична прогресія

, , d = ?

1. 4   b) -4   c) 8  d) 12

Група 3

1. Дано арифметичну прогресію 32; 16; …

Знайти

1. -16  b) 16   c) 48   d) 0

2. Дано арифметичну прогресію 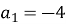 , , 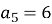Знайти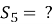

а) 2  b) -10  c) 5    d) -5

3. Дано арифметичну прогресію ,

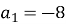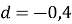
Знайти

a)-9,2  b) -33,4  c) 44  d) -6,8

 

За результатами відповідей складемо слово. Таблиця відповідей.

 

Г	Е	С	І	Р	О	П	Я	Н
42	-4	0	5	-8	-44	6	-9,2	4

 

Сторінкиісторії. (повідомленняучня)

 

      Історія  арифметичної прогресії

Термін «прогресія» був уведений римським автором Боецієм ще в IVст. н.е. Від латинського слова progressio – «рух вперед».

Перші спогади про арифметичн упрогресіюбули ще у прадавніх народів. У клинописних вавилонських табличках і єгипетських папірусах зустрічаються задачі на прогресії та вказівки як їхрозв’язувати. Вважалось, що в давньоєгипетському папірусі Ахмеса перебувала найдавніша задача на прогресії про винагороду винахідника шахів, що нараховує за собою двохтисячорічну давнину. Але є набагато більш стара задача про ділення хліба, яка записана в знаменитому єгипетському папірусі Райдана. Папірус цей, розшуканий Райданом піввіку назад, складений близько 2000 років до нашої ери і є списком з іншого, ще більш, прадавнього математичного твору, що відноситься, можливо, до третього тисячоліття до нашої ери.

 

«Прогрес» - рух вперед.

Саме рух вперед змушував математиків різних часів здійснювати різні відкриття.

Сьогодні ми з вами будемо рухатися вперед і переконаємося, що розділ математики  «Прогресії» є невід’ємною частиною загальнолюдської  культури і оточуючого нас світу.

Спробуємо відповісти на питання, навіщо нам потрібні отримані знання, і де в повсякденному житті ми можемо зустріти арифметичну прогресію?

 

IV. Застосування знань про арифметичні прогресії в інших областях.

Діти, до сьогоднішнього уроку кожній групі було задано домашнє завдання: знайти матеріал про застосування арифметичної прогресії в житті. Першими послухаємо групу, яка шукала зв’язок між арифметичною прогресією і літературою.

 

Математика і поезія. Хіба може їх щось пов’язувати? Вони такі різні

Вчений стародавнього сходу Омар Хайям писав складні праці з математики, а на полях писав вірші.

Писала вірші й жінка-математик С.В. Ковалевська, а про математику вона говорила так: «Не можна бути математиком, не будучи в той же час поетом у душі». Згадаймо рядки з твору «Євгеній Онєгін»: Не міг він ямба від хорея, як ми не бились відрізнити… Ямб – це віршований розмір з наголосом на парних складах 2; 4; 6; 8… Номери наголошених складів утворюють арифметичну прогресію з першим членом 2 і різницею прогресії 2. Наприклад, ямб: «Мій дядя самих чесних правил»; «Садок вишневий коло хати».

Хорей – це віршований розмір з наголосом на непарних складах вірша. Номери наголошених складів утворюють арифметичну прогресію 1; 3; 5; 7… з першим членом 1 і різницею прогресії 2. Наприклад, хорей: «Думи мої, думи мої, лихо мені з вами».

Висновок: Математика та література не так далекі один від одного, як багато хто думає.

Слово надається учням 2групи, які встановлювали зв’язок арифметичної прогресії з біологією.

Задача 1:Висота саджанця 60 см, перші півроку вона збільшується щомісяця в середньому на 4 см. Яким буде висота саджанця через 6 місяців?

Дано: ( – прогресія, . Знайти - ?

Розв’язання:

Відповідь: 80 см

Висновок: Рослини – біологія, а розв’язали ми завдання, застосовуючи знання про арифметичну прогресію.

 

Слово надається учням 3 групи, які встановлювали зв’язок між арифметичною прогресією і фізикою.

Задача 2:Гальмуючи, автомобіль за першу секунду проїхав 15 м, а за кожну наступну – на 3 м менше, ніж за попередню. Знайдіть гальмівний шлях автомобіля.

Дано:

Знайти: -?

Розв’язання:

Відповідь: 45 м

Індивідуальне завдання:Автомобіль, рухаючись зі швидкістю 1 м/с за кожну наступну секунду змінював свою швидкість на 0,6 м/с. Яку швидкість він матиме через 10 секунд?

Дано:

Знайти: -?

Розв’язання:

Відповідь: 6,4 м/с

 

Індивідуальне завдання:При вільному падінні тіло проходить в першу секунду 5м, а в кожну наступну на 10м більше. Знайдіть глибину шахти, якщо вільно падаюче тіло досягло її дна через 5с після початку падіння.

 

Дано: ( – прогресія, . Знайти - ?

 

Розв’язання:

Відповідь: 125м

 

Наступна група 4 познайомить нас зі своїм дослідженням. Спробує зв’язати арифметичну прогресію з медициною.

 

Задача 3. Кількість еритроцитів (з розрахунку на 1) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м піднімання вгору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест висота якої 4800м.

 

Дано:

Знайти: -?

Розв’язання:

Відповідь:

 

Завдання: Відпочивальник, слідуючи пораді лікаря, у перший день засмагав

5 хвилин. На який час перебування на сонці дорівнюватиме 40 хвилин?

Відповідь:на 8 день.

 

Я теж підготувала вам життєве завдання:

 

Завдання: Юнак подарував дівчині в перший день 3 квітки, а в кожний наступний день дарував на 2 квітки більше, ніж у попередній день. Скільки подарував квітів юнак за два тижні?

 

Дано: ( – прогресія, .

Знайти - ?

Розв’язання:

                        Знайдемо кількість квіток, куплених за два тижні.

Відповідь: 224 квітки.

 

Сьогодні на уроці ми навчилися застосовувати знання про арифметичну прогресію для вирішення життєвих завдань.

 

V. Підсумки уроку.

 

На цьому етапі визначити, чи досягнуті мета, очікувані результати уроку, провести рефлексію. Учням пропонується дати відповіді на запитання таблиці та заповнити листи самооцінювання і здати вчителеві, який підбиває підсумок уроку, оголошує оцінки.

 

 

 

 

 

 

 

Таблиця для рефлексії

 

	так	не зовсім	ні
Я розумію і знаю:
Що таке арифметична прогресія
Різниця арифметичної прогресії
Зростаюча та спадна АП
Я вмію: Знаходити різницю d арифметичної прогресії
Знаходити суму АП
n-ий член АП
Я вчився сам: Пояснювати, щоб всі зрозуміли Розуміти пояснення іншого Працювати в групі Не відволікатись Не заважати іншим Я досяг успіху!!!

 

 

Домашнє завдання:

1)Повторити означення арифметичної прогресії, її властивості, формули, вивчені у темі «Арифметична прогресія».

    2) Скласти та розв’язати дві прикладні задачі, в яких можна застосовувати арифметичну прогресію.

 

Урок сьогодні завершено, але кожен повинен знати:

Пізнання, завзятість, праця – до прогресу в житті приведуть.