Урок з алгебри по темі "Раціональні вирази". 8 клас

Тема. Раціональні вирази. Алгебра. 8 клас

Мета: систематизувати та узагальнити знання учнів з теми «Раціональні вирази. Раціональні дроби. Основна властивість дробу. Додавання і віднімання раціональних дробів»; формувати навички розв’язування вправ по темі;

 сприяти активізації пізнавальної діяльності учнів; зацікавити учнів проектом, вчити самостійно працювати над творчими завданнями;

 виховувати почуття доброти, співчуття, бажання прийти на допомогу, вміння працювати групами, цікавість до предмета.

Тип уроку: узагальнення та систематизація знань і вмінь

Наочність та обладнання: опорні схеми, роздавальний матеріал для «Математичного лото», комплект тестових завдань, роздавальний матеріал для груп, проектор, таблиця-ключ

 

«Не успіх, а зусилля заслуговують нагороди» Джон Рескін

 

Хід уроку

І. Організаційний етап

Учні розмістилися за партами для роботи в групах

ІІ. Перевірка домашнього завдання

Відповісти на запитання, які виникли в учнів при виконанні вправ домашнього завдання. Наприкінці уроку зібрати зошити

 

ІІІ. Мотивація навчальної діяльності

Шановні учні! Ми з вами закінчили вивчати теоретичний матеріал з теми «Раціональні вирази. Раціональні дроби. Основна властивість дробу. Додавання і віднімання раціональних дробів». Сьогодні наша мета узагальнити і систематизувати набуті знання з теми, повторити правила, означення, закріпити набуті вміння та навички.

Досягнути нашої мети нам допоможуть «Юні математики», «Трикутнички», «Дружба знаків», «Усмішка» (групи піднімаються по черзі з місць). Кількість груп дорівнює кількості тем, які нам треба повторити. Кожна група підготувала свій проект і сьогодні ми проводимо їх захист.

Але спочатку прослухаємо історичну довідку.

Сучасне позначення дробів бере свій початок у Стародавній Індії. Його стали використовувати й араби, а від них у ХІІ-ХІV ст. було запозичено європейцями. Спочатку в запису не використовувалась дробова риска. Риску дробу стали постійно застосовувати лише близько 300 років тому.

Першим європейським вченим, який став використовувати і розповсюджувати у 1200 році сучасний запис дробів, був італійський купець і мандрівник Леонардо Пізанський. Він увів слово «дріб». Назву чисельник і знаменник увів у ХІІІ столітті Максим Пеаунд – грецький монах, учений-математик

 

IV. Узагальнення і систематизація знань і вмінь

Першими презентують свій проект «Юні математики»

Презентація проекту «Дробові вирази. Раціональні вирази»

«Теоретики»

Раціональним виразом називається вираз, який складається з чисел і букв, що з’єднуються знаками дій додавання, віднімання, множення, ділення та дужками

Значення змінних, при яких дріб має зміст, називають допустимими значеннями змінних.

 

«Дослідники»

Цілий вираз має зміст при будь-якому значенні змінних, що входять до нього.

Дріб дорівнює нулю, якщо чисельник дорівнює нулю, а знаменник не дорівнює нулю.

Щоб знайти значення змінної, при якому раціональний дріб дорівнює нулю, треба:

1. знайти ОДЗ дробу;
2. прирівняти чисельник дробу до нуля і знайти відповідні значення змінних;
3. із знайдених значень змінних вилучити ті, які не входять в ОДЗ.

 

«Практики»

При якому значенні змінної дріб дорівнює нулю?

Розв’язання:

1. ОДЗ: ;
2. ;
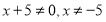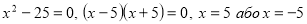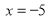3. не входить в ОДЗ, тому при 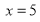даний дріб дорівнює нулю.

 

А тепер група «Юні математики» пропонує іншим групам завдання, розв’язавши які вони назвуть подію минулого тисячоліття.

Завдання

1. Знайти значення змінної, при якому дріб 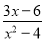не має змісту.
2. Знайти значення змінної, при якому дріб 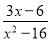дорівнює нулю.
3. Знайти значення дробу .

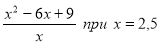Таблиця-ключ

2	-2	-2; 2	10	0,1	1
1	7	8	6	4	5

 

Відповідь: 1814 р. народився Т.Г. Шевченко.

 

Група 2 «Трикутнички»

Презентація проекту «Основна властивість дробу»

«Теоретики»

Якщо чисельник і знаменник дробу помножити або поділити на один і той самий вираз, відмінний від нуля, то одержимо дріб тотожно рівний даному.

 

Ділення чисельника і знаменника дробу на їх спільний множник називається скороченням дробу.

 

«Дослідники»

Щоб скоротити дріб треба:

1. розкласти чисельник і знаменник дробу на множники;
2. визначити спільний множник для чисельника і знаменника;
3. поділити чисельник і знаменник дробу на їх спільний множник;
4. записати тотожну рівність з урахуванням ОДЗ початкового дробу.

 

«Практики»

Скоротити дріб .

Розв’язання:

.

Ми, «Трикутнички», пропонуємо вам гру «Математичне лото». Склавши його, ви одержите малюнок.

Скоротити дроби

 

 

 

 

 

Група 3 «Дружба знаків»

Презентація проекту «Додавання і віднімання раціональних дробів з однаковими знаменниками»

«Теоретики»

Щоб додати раціональні дроби з однаковими знаменниками, потрібно додати їх чисельники, а знаменник залишити без змін.

 

Щоб відняти раціональні дроби з однаковими знаменниками, потрібно від чисельника зменшуваного відняти чисельник від’ємника, а знаменник залишити без змін.

 

«Дослідники»

Дроби із протилежними знаменниками додають (віднімають) за правилом, що виражається формулою:

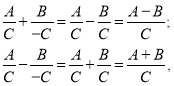
де А, В, С – многочлени,

 

«Практики»

Спростити вираз:

Розв’язання:

.

 

Виконавши наші завдання, ви дізнаєтесь, хто прийшов до того ж відкриття, що й Рене Декарт (створив систему координат), яка все ж таки носить ім’я Декарта, та указав на зв’язок алгебри з геометрією.

 

 

Спростити вирази:

	А	Б	В	Г
1)
2)
3)
4)
5)

 

Таблиця-ключ

	А	Б	В	Г
1	О	Н	П	Ф
2	У	А	Е	М
3	Р	К	И	Д
4	І	М	Ф	К
5	А	Б	Ж	Й

 

Відповідь: Ферма

 

Група 4 «Усмішка»

Презентація проекту «Додавання і віднімання дробів з різними знаменниками»

«Теоретики»

Дроби із різними знаменниками додають (віднімають) за правилом, що виражається формулою: , де А,B,C,D – многочлени,

 

«Дослідники»

Щоб додати (відняти) дроби з різними знаменниками, треба:

1. знайти спільний знаменник дробів (бажано найменший);
2. звести дроби до спільного знаменника;
3. додати або відняти одержані дроби;
4. спростити дріб, якщо це можливо.

 

«Практики»

Спростити вираз .

Розв’язання:

Група «Усмішка» доводить до вашого відома, що з давніх-давен числа наділяли різноманітними властивостями. Число 7 вважалося щасливим. У багатьох народів число 7 увійшло до легенд, прислів’їв та приказок як синонім чогось великого та непорушного. Що сказав про числа давньогрецький філософ Платон? Дати відповідь на це запитання вам допоможуть правильні відповіді до наших завдань.

Спрости вирази:

Таблиця-ключ

ЛА	МО	БО	НИЗ	ЧИС	ПРО	ПА	ЦЕ	РИ	ГИ
						4

 

Відповідь: «Числа – це боги»

 

Група, яка дає завдання іншим групам, слідкує за правильністю їх виконання.

 

V. Підсумок уроку

Використовується метод ділової гри «Мікрофон». Учні дають відповіді на запитання вчителя:

• Що ми робили на уроці?
• Для чого ми це робили?
• Чи досягли своєї мети?
• Чи сподобався вам спосіб проведення уроку?
• Що не сподобалося?

 

VІ. Домашнє завдання

Повторити §§ 1-4, розв’язати індивідуальні завдання на картках