Урок алгебри та початків аналізу 11 клас

Тема уроку. Розв'язування логарифмічних рівнянь та нерівностей.

Мета уроку: 

Навчальна : відпрацювати навички розв'язування логарифмічних рівнянь та нерівностей; 

Розвивальна: сформувати вміння вибору методів розв'язування логарифмічних рівнянь та нерівностей; розвивати навички самоконтролю; пам'ять, увагу, культуру математичного запису,

Виховна: виховувати інтерес до математики, наполегливість, акуратність.

Очікувані результати: учні повинні вміти розв'язувати логарифмічні рівняння та нерівності різними методами.

Обладнання:  підручник, роздатковий матеріал, презентація, листи самоконтролю

Тип уроку: застосування знань і вмінь.

Хід уроку

І. Організаційний етап.  Перевірка готовності учнів до уроку

ІІ. Перевірка домашнього завдання

На екран проектуються завдання,  які учні виконували вдома. Учитель фронтально опитує учнів.

loq₂x2 loqx_2

loq₄ x² 2 loq3(6−x)−2 loq3(2x+1)loq3(x−4)

Оцінювання учнів

ІІІ.  Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності.

Нам  потрібно відпрацювати навички розв'язування логарифмічних рівнянь та нерівностей; сформувати вміння вибору методів розв'язування логарифмічних рівнянь та нерівностей ;розвивати навички самоконтролю; культуру математичного запису.

ІV Актуалізація опорних знань Математичний штурм

1)    Що називається логарифмічним рівнянням?

2)    Що називається логарифмічною нерівністю?

3)    Властивості та формули логарифмування

4)    Методи розв'язування логарифмічних рівнянь та нерівностей.

5)    Властивості логарифмічних функцій при розв'язуванні логарифмічних нерівностей

Парна робота з перевіркою  «Вірно-невірно» по рядам                                           

Оцінювання учнів.

V   Удосконалення  вмінь та навичок

     Для розв’язування більш складних рівнянь потрібно знати основні методи розв'язування логарифмічних рівнянь.

Колективна усна робота

Установіть відповідність між методами розв'язування та логарифмічними  рівняннями, не рівностями (ЗНО)

Відповіді: 1в; 2г; 3а;4е;5б;6д.

Оцінювання учнів.

VІ. Застосування вмінь та навичок 

1)  Попарно  розв’язати логарифмічні рівняння.

Оцінювання учнів.

2)  Колективне розв’язання усної вправи «Знайди помилку» 

Знайди помилку:

1) log (x +3)+log₂(x + 2)= log6                    2)           lg(4x − 3) = 2 lg x

4x − 3 = 2

             (x +3)(x + 2)= 6

4x = 5

 x² +5x +6 = 6           ₅ x² = 0,x = −5          ^{x =} ₄

Оцінювання учнів.

3)  Колективне розв’язання логарифмічних нерівностей. 

Опрацювання завдань ЗНО

4)  Укажіть кількість цілих розв’язків нерівностей 

log₅ ( х − 6 ) + log₅( х − 5 ) ≤ 1 + log₅ 4

Оцінювання учнів

VІІ.. Домашнє  завдання. Розв’язати рівняння

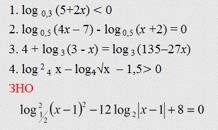
VІІІ Підсумок уроку

 Позаду наш урок: логарифми, рівняння. А попереду – все життя. 

Нехай ваша наполегливість, ваші уміння і бажання добитися поставленої мети допоможуть вам стати справжніми майстрами своєї справи. 

І пам’ятайте вислів Оноре де Бальзака « Щоб дійти до мети,  треба перш за все іти.»  

Додатки 

Листок самоконтролю   Прізвище,імя ____________________________________________________