Урок з геометрії для учнів 9 класу на тему: "Метод площ"

Міністерство освіти та науки України

Відкритий урок

за темою:

Метод площ

проведений у 9 класі

вчителем математики

Задорожною Світланою Миколаївною

КЗО «Гімназія № 3» ДМР

2020 рік

Тема уроку:       Метод площ

Мета уроку: Ознайомити учнів з основними прийомами розв’язування задач методом площ. 

                       Навчити встановлювати зв'язок між відношенням в якому ділиться відрізок

                       трикутника з відношенням площ деяких трикутників. Сформувати уміння

                       отримувати відношення між різними геометричними величинами, виражаючи їх

                       через площі. Вміти застосовувати набуті знання при розв’язанні задач різного

                       рівня складності. Розвивати уміння аналізувати, робити висновки, будувати

                       аналогії, узагальнювати набуті знання. Виховувати культуру математичної мови,

                       формувати наполегливість у досягненні мети, гуманні відносини між учнями на

                       уроці.

Тип уроку:    Урок засвоєння нових знань.

Хід уроку.

Епіграфом до нашого уроку будуть слова видатного Галілео Галілея:

                                                 „Природа говорить мовою геометрії:

                                                   букви цієї мови – кола, трикутники

                                                   та інші геометричні фігури”

                                                                              / Галілео Галілей /

I. Мотивація учбової діяльності учнів на уроці.

        Сьогодні на уроці ми розширимо коло вивчаємих планіметричних понять, таких як  трикутник, медіана, висота, площа отримуючи відношення  між різними геометричними величинами та виражаючи їх через площу. Тобто тема сьогоднішнього уроку: „Метод площ”.

Виходячи з теми уроку, я хотіла б почути ваші очікування від уроку ? Чим буде корисним для нас цей урок?

1 учень: На уроці ми будемо застосовувати раніше отримані знання при розв’язанні різних задач.

2 учень: На уроці ми будемо вдосконалювати повторені поняття..

3 учень: Ми на уроці отримаємо тільки гарні оцінки.

II. Засвоєння нових знань.

Спочатку ми встановимо зв'язок між відношенням в якому ділиться сторона трикутника з відношенням площ деяких трикутників.

Завдання класу: Нехай відрізок, що з’єднує вершину С трикутника АВС з точкою Р на протилежній стороні, ділить цю сторону у відношенні АР : РВ. В якому відношенні ділить цей відрізок площу трикутника АВС?

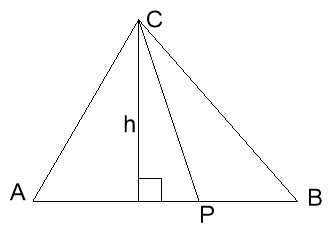
Розв’яжіть задачу, заповнивши пропуски:

________, а _________. Розділимо першу рівність на другу: .

Отже, ми довели твердження:

„Відрізок, що з’єднує вершину С трикутника АВС з точкою Р на протилежній стороні, ділить його площу в тому ж відношенні, в якому цією точкою Р ділиться протилежна сторона АВ:

.”

Доведення: , а . Розділивши першу рівність на другу, отримаємо , що .

Ці ж міркування справедливі і для точки, що лежить на продовженні протилежної сторони.

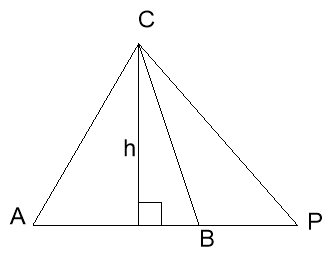
Завдання класу: Нехай медіани трикутника АВС перетинаються в точці М. Доведіть властивість медіан трикутника за допомогою площ.

Теорема: „Медіани трикутника, точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини”.

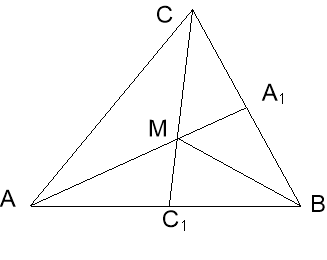
Доведіть теорему, заповнивши пропуски:

 Треба довести, що СМ : МС₁ = _:_ . За доведеним вище маємо, що . Аналогічно, , звідси . Аналогічно, трикутники МАС і _____ рівновеликі, тому,

.

Застосовуючи наше твердження, маємо:

.

Доведення теореми: Треба довести, що СМ : МС₁ = 2 : 1. За доведеним вище маємо, що . Аналогічно, , звідси . Аналогічно, трикутники МАС і МАВ рівновеликі, тому,

. Застосовуючи наше твердження, маємо: .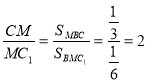

  Твердження про відношення площ трикутників можна узагальнити. Отримаємо першу лему про площі або лему про площі трикутників зі спільною основою:

„ Якщо пряма, що з’єднує вершини С і С₁ трикутників АВС і АВС₁ зі спільною стороною АВ перетинає пряму АВ в точці Р, то відношення площ трикутників дорівнює відношенню, в якому точка Р ділить відрізок СС₁, що з’єднує їх вершини: .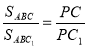

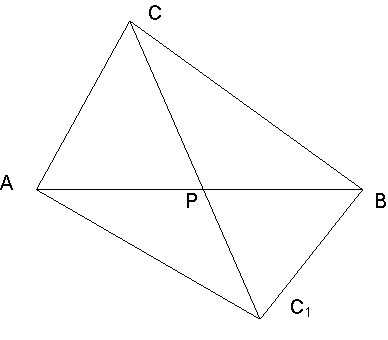
Доведення: Відношення площ даних трикутників АВС і АВС₁ дорівнює відношенню їх висот СН і СН₁, що проведені до спільної сторони АВ:

.

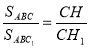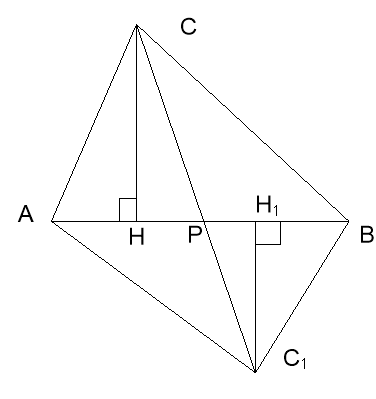
Прямокутні трикутники СНР і С₁Н₁Р подібні, так як їх кути при вершині Р рівні. Висоти є відповідними катетами цих трикутників. Тому їх відношення дорівнює відношенню гіпотенуз СР і СР₁. Що і треба було довести.

Завдання класу (робота в парах): Виберіть з відношень відрізків АК : КС, АМ : МВ, LР : РА,

 СМ : РМ ті, які дорівнюють відношенню площ вказаних трикутників:

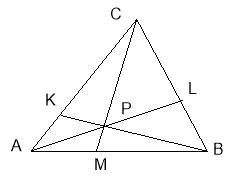
Розв’яжи задачу, заповнивши пропуски:

1) ____:____, (АК : КС)

2) ____:____,  (АК : КС)

3) ____:____,  (СМ : РМ)

4) ____:____,  (АМ : МВ)

5) ____:____.  (PL : РА)

Застосуємо першу лему площ для доведення теореми Чеви.

Теорема: „Нехай в трикутнику АВС сторони АВ, ВС і АС діляться точками К, L і М відповідно в певному відношенні, тоді ”.

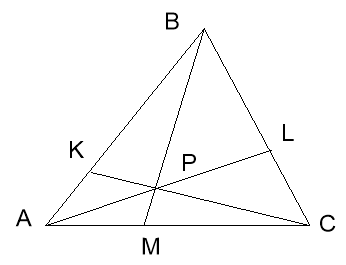
Задум доведення полягає в тому, щоб виразити відношення між прямими АР, ВР і СР через відношення площ трикутників РВС, РСА і РВА.

.

Доведення теореми проведіть заповнивши пропуски:

Виразимо відношення, в яких діляться сторони трикутника через відношення площ k,l і m трикутників РАВ, РВС і РСА

, .

Доведення теореми Чеви методом площ.

Виразимо відношення, в яких діляться сторони трикутника через відношення площ k,l і m трикутників РАВ, РВС і РСА

, .

Доведем цим же способом теорему Мєнєлая.

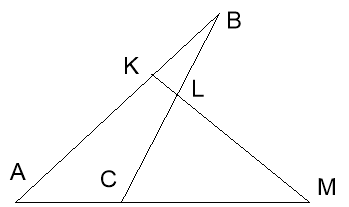
Теорема: „Нехай пряма перетинає сторони трикутника АВС або їх продовження у точках К,L,М. Треба довести, що добуток тих же відношень, що і у теоремі Чеви, дорівнює одиниці:

”.

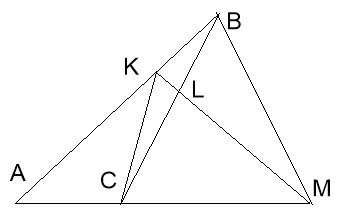
Проведемо допоміжні лінії ВМ і СК. Тоді ці відношення можна представити, як відношення площ деяких трьох трикутників. Ці трикутники знайдіть самостійно.

Підказка: Знайдіть на рисунку такі три трикутника, з площами S₁, S₂, S₃,щоб виконувалось співвідношення:

Доведення теореми проведіть заповнивши пропуски:

Такими трикутниками з площами S₁, S₂, S₃ будуть трикутники ___, ___  та ___ відповідно.

Отже, .

Доведення:

Такими трикутниками з площами S₁, S₂, S₃ будуть трикутники АКМ, ВКМ та СКМ відповідно.

Отже, .

Метод, яким ми довели теореми Чеви  та Мєнєлая називається методом площ. Задум цього метода полягає в тому, щоб отримувати відношення між різними геометричними величинами, виражаючи їх через площі.

Задача класу: Відрізки АК, BL і СМ, що з’єднують вершини трикутника АВС з точками на протилежних сторонах, перетинаються в точці Р в середині трикутника. Відомо, що ВР=2РL, СР=РМ. Знайти відношення КР : РА?

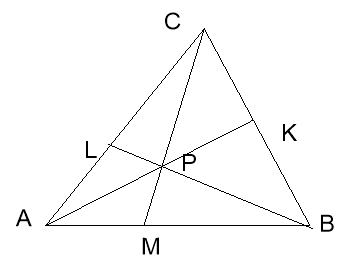
Розв’яжіть задачу, заповнивши пропуски:

Позначимо через S₁, S₂, S₃ площі трикутників ВСР, САР, АВР. Їх сума дорівнює площі S всього трикутника АВС, тобто ___________ = S.  Розділимо обидві частини рівності на S. 

Маємо: --- + --- + --- = 1. Якщо замінити відношення площ на відношення відповідних відрізків з леми про площі, то отримаємо рівність: --- + --- + --- = 1.

Розв’язання: Позначимо через S₁, S₂, S₃ площі трикутників ВСР, САР, АВР. Їх сума дорівнює площі S всього трикутника АВС: S₁+ S₂+ S₃= S. Тому,

. Якщо замінити відношення площ на відношення відповідних відрізків з леми про площі, то отримаємо рівність:

.

 Отримане відношення називається теоремою Жаргонна.

Доданки в його лівій частині виражаються через відношення, про які говориться в нашій задачі. Наприклад,

BL = BP+PL = 2PL + PL = 3PL.

,

.

Поряд з лемою про площу трикутника зі спільною основою, часто використовують другу лему про площі або лему про площі трикутників зі спільним кутом: „Відношення площ трикутників, що мають спільний кут, дорівнює відношенню добутку сторін, що утворюють цей кут”.

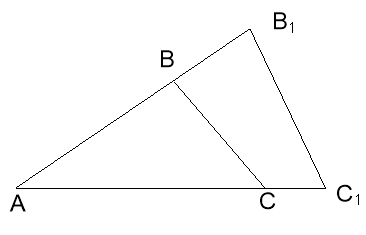
Доведення проведіть заповнивши пропуски:

Нехай у трикутниках АВС і АВ₁С₁ кут А спільний. Так як ,   а   , тоді матимемо:

, що і треба було довести.

Доведення: Нехай у трикутниках АВС і АВ₁С₁ кут А спільний. Так як ,   а   , тоді матимемо:

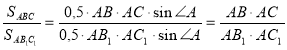, що і треба було довести.

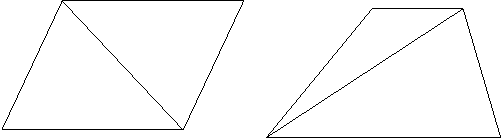
Обидві леми про площі працюють і в задачах про паралелограми та трапеції. Потрібно перейти від чотирикутників до трикутників, на які вони розбиваються однією з діагоналей.

III. Фізкультхвилинка

Зараз ми з вами трохи порухаємося. Піднімемося, покладемо руки на плечі сусіда. Уявимо собі, що ми знаходимося у країні Геометрії, яка розташована в теплій Греції.

„Сьогодні в країні Геометрії гарна погода:

світить сонечко ( погладити плечі  ),

подув легенький вітерець ( рухи руками вліво, вправо ),

пішов дрібненький дощик ( постукати пальцями по спині легко ),

пішов град ( постукати пальцями по спині сильніше ),

посипалося каміння ( постукати кулаками по спині ),

пішов град ( постукати пальцями по спині сильніше ),

пішов дрібненький дощик ( постукати пальцями по спині легко ),

подув легенький вітерець ( рухи руками вліво, вправо ),

світить сонечко ( погладити плечі  ),

на всій території Геометрії гарна погода.”

IV. Формування вмінь та навичок.

Розв’язування задач по групам.

Клас розбивається на групи і кожна група отримує однакове завдання по три задачі.  Перша задача на 4 -6 балів, друга задача на 7 – 9 балів, і третя задача  – на 10 -11балів.

Задача № 1 (4 -6 б): У трикутнику АВС проведені відрізки AL і ВК від вершин А і В до протилежних сторін, що перетинаються в точці Р. Відомо, що АК: КС = 1:2, ВL : LС = 1:3. Знайти відношення площ трикутників АВР і АВС?

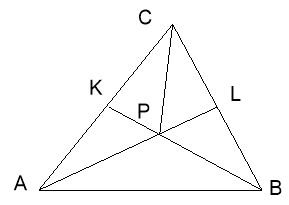
Заповніть пропуски в розв’язанні задачі: Нехай площа трикутника АВР дорівнює S. Тоді

, тобто . Далі , тобто . Отже, і тому .

Розв’язання:

Нехай площа трикутника АВР дорівнює S. Тоді , тобто . Далі , тобто . Отже, і тому .

Відповідь: .

Задача № 2 ( 7 – 9 б): На сторонах трикутника АВС, площею 1 обрано точки А₁, В₁, С₁, так, що ВА₁:А₁С = 2:1,  АС₁:С₁В = СВ₁:В₁А= 1:5. Чому дорівнює площа трикутника А₁В₁С₁, якщо площа трикутника АВС дорівнює 1?

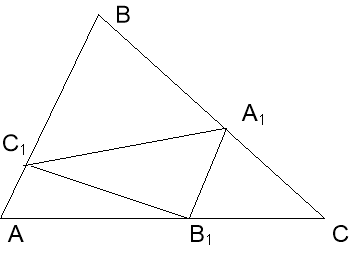
Заповніть пропуски в розв’язанні задачі: Так як СВ₁:В₁А= 1:5, то АВ₁: АС = ___, аналогічно АС₁: АВ = ____. Тому = _____ . Таким же чином, знайдемо, що  площа трикутника ВА₁С₁ = ____, а площа трикутника СВ₁А₁= ____ .

Отже, отримаємо відповідь _______.

Розв’язання:

За другою лемою про площі, маємо:

,

,

. Звідси, .

Відповідь: .

Задача № 3 ( 10 – 11 б): У трикутнику АВС проведені відрізки AL і ВК від вершин А і В до протилежних сторін, що перетинаються в точці Р. Відомо, що АК: КС = 3:2, ВР : РК = 5:3. Знайдіть площу чотирикутника СLРК, якщо площа трикутника АВС дорівнює 40?

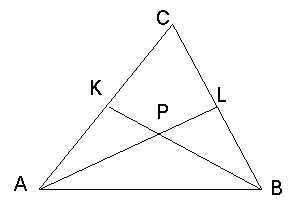
Розв’язання: Нехай х – площа трикутника АРК, тоді площа трикутника АРВ дорівнює , а площа трикутника СКР дорівнює . Очевидно, що трикутник АРС рівновеликий з трикутником АВР. За першою лемою про площі випливає, що BL = LC. За другою лемою відношення площ трикутників BLP і ВСК дорівнює відношенню добутків їх сторін зі спільною вершиною В, тобто . Отже, площа чотирикутника CLPK становить площі трикутника ВСК, яка в свою чергу дорівнює площі трикутника АВС.

.

Відповідь: 11.

Після закінчення розв’язування задач результати групової роботи обговорюються біля дошки. Кожен учень з групи отримує оцінку.

Робота біля дошки:

Перший учень отримує завдання на 4 – 6 балів.

 Задача: Доведіть, що в будь-якому чотирикутнику ABCD добуток площ S₁ і S₂ трикутників АОВ і СОD, де О – точка перетину діагоналей чотирикутника, дорівнює добутку площ S₃ і  S₄ трикутників ВОС і DОА.

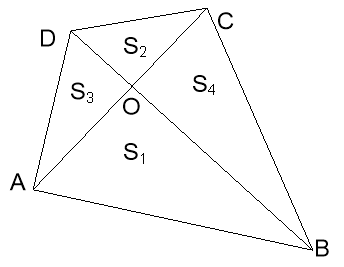
Користуючись першою лемою про площі маємо:

.

Другий учень отримує завдання на 7 – 9 балів.

Задача: Нехай точка L  ділить сторону АВ паралелограма АВСD, площею 1 у відношенні 2:1, а точка К ділить сторону DC у відношенні 1:4. Знайдіть площу трикутника ALK?

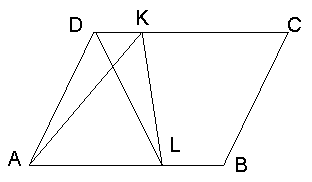
Розв’язання: Так як трикутник ALK має спільну сторону з трикутником ALD, а пряма  KD паралельна цій стороні, то площі цих трикутників рівні. Далі,

, бо . Трикутник АВD становить половину паралелограма, тому шукана площа трикутника АLK дорівнює площі паралелограма. Зверніть увагу на те, що відповідь не залежить від розташування точки К на стороні ВС. Іноді в задачах бувають зайві данні.

Третій учень отримує завдання на 10 -11 балів.

Задача: Знайти площу трапеції, якщо площі трикутників обмежених її діагоналями і основами, рівні 16 та 9.

Розв’язання:

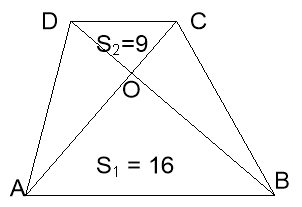
Відомо, що відношення площ подібних фігур дорівнює квадрату коефіцієнта подібності. Так як трикутники АОВ і СОD подібні, то

k = . Тоді користуючись першою лемою про площі, маємо:

, .

.

Відповідь: 49.

V. Підсумки уроку.

Питання класу : Що нового ви узнали сьогодні на уроці?

1 учень:  Ми ознайомилися з методом площ.

2 учень: Ми навчилися застосовувати метод площ при розвязуванні задач.

3 учень: Найкращих результатів можна досягти працюючи в групах.

4 учень: Треба поважати особисту думку один одного.

VI.  Домашнє завдання

Диференційоване домашнє завдання.

I) на  4-6 балів.

1) У трикутнику АВС на сторонах АС і СВ взято точки К і L відповідно. Відрізки АL і КВ перетинаються в точці Р і діляться цією точкою у такому відношенні АР : РL = 3 : 4, ВР : РК = 6. Знайдіть відношення площ трикутників ВРL та АВС.

Відповідь: 8 : 21.

2) Знайдіть число таких точок М у площині трикутника АВС, для яких трикутники АМВ, ВМС і СМА – рівновеликі.

Відповідь: 4.

II) на 8 балів.

3) В площині паралелограма АВСD, площею 8 дана точка Р. Прямі АР і DР перетинають сторони ВС і АВ відповідно у точках F і Е, так, що АЕ = 3ЕВ, BF = 2 FC. Знайдіть площу чотирикутника BFPE.

Відповідь: .

III) на 10 балів.

4) З точки D на стороні АВ трикутника АВС проведені прямі паралельні двом іншим сторонам. Площі трикутників, що відтинаються цими прямими, дорівнюють 3 і 12. Знайдіть площу трикутника АВС.

Відповідь: 27.

IV) на 12 балів.

5) Площа трапеції дорівнює 30. Точка Р – середина бічної сторони АВ. Точка R належить стороні СD так, що 2С D = 3 RD. Прямі AR і PD перетинаються в точці Q. Знайдіть площу трикутника APQ, якщо AD = 2BC.