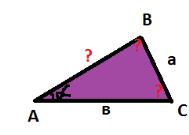
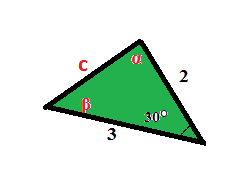
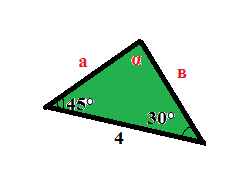
Урок "Розв'язування трикутників"
Загальноосвітня школа І-ІІІ ступенів с.Велика Яблунька
Розв’язування трикутників
Урок геометрії в 9 класі
Вчитель Радчук Т.С.
2020
Тема. Розв’язування трикутників
Мета: узагальнити матеріал про теореми косинусів і синусів; розглянути основні види задач, у яких вимагається розв’язати трикутник;
розвивати навички розв’язування трикутників,
розвивати вміння виділяти головне, розвивати логічне мислення;
виховувати акуратність при виконанні побудов і записах у робочому зошиті, дисциплінованість
Очікувані результати: учні повинні чітко визначати, яку теорему використати, вміти застосовувати формули теорем косинусів і синусів до розв’язування задач.
Компетентності, що формуються: математична – уміння оперувати геометричними об’єктами, використовувати формули теорем синусів і косинусів; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; уміння вчитися впродовж життя.
Обладнання: комп’ютер, інтерактивна панель
Тип уроку: урок-змагання (конфлікт теорем)
Хід уроку
І. Організаційний етап.
ІІ. Перевірка домашнього завдання.
На інтерактивній панелі висвітлюється розв’язання домашніх задач. Учні звіряють із своїми записами і відповідями.
ІІІ. Актуалізація опорних знань.
Мозковий штурм
- Яка теорема записується формулою с²=а²+в²-2 а·в·cosC ? (Теорема косинусів)
-
 =
=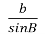 =
=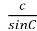 ? (Правильно)
? (Правильно)
-
Як знайти катет а прямокутного трикутника АВС, якщо відомі гіпотенуза с і катет в? (а=
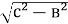 )
)
- Визначити вид кута А, якщо а²<с²+в² (Кут А – гострий).
-
Чому дорівнює
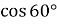 ? (
? (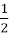 )
)
ІV. Повідомлення теми і мети уроку
Сьогодні на уроці ми будемо вивчати тему «Розв’язування трикутників». У 8 класі ви вивчали теорему Піфагора, яку використовували для розв’язування задач на обчислення елементів прямокутного трикутника. Ці задачі є окремими випадками задач, які прийнято називати задачами на розв’язування трикутників.
V. Сприймання та усвідомлення нового матеріалу
Існують такі види задач, у яких вимагається розв’язати трикутник: 1) за двома сторонами і кутом між ними; 2) за стороною і прилеглими до неї кутами; 3) за трьома сторонами; 4) за двома сторонами й кутом, прилеглим до однієї з них.
Вдома ви опрацьовували параграф 13. Для кращого засвоєння теми, проведемо урок-змагання ( конфлікт теорем) між командами :
І команда - «Косинуси» і ІІ команда - «Синуси».
Інформацію ваших команд подамо у вигляді таблиці.
|
Вчитель |
І команда «Косинуси» |
ІІ команда «Синуси» |
|
Сформулюйте свої теореми |
Квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін без подвоєного добутку цих сторін на косинус кута між ними |
Сторони трикутника пропорційні до синусів протилежних кутів |
|
Запишіть формули |
с²=а²+в²-2 авcosC |
|
|
Де вперше появилась згадка про дані теореми (історична довідка) |
Теорема косинусів була відома ще стародавнім грекам: її доведення міститься у II книзі найстарішого грецького математичного трактату «Начала» грецького математика Евкліда. |
Вперше теорему синусів довели у X-XI століттях математики Близького і Середнього Сходу.
|
|
Переваги формул |
Ліва і права частина – цілі вирази |
Можемо з однієї рівності утворити три
|
|
|
За таблицею синусів і косинусів досить знайти лише одне значення cosC |
Хоча нам знайти два значення
їх по таблиці легше визначати |
|
|
Ми можемо за сторонами трикутника визначити його вид: кут А – гострий, якщо а²<в²+с², кут А – прямий, якщо а²=в²+с², кут А – тупий, якщо а²˃в²+с², |
Ми маємо два наслідки:
1.У будь-якому трикутнику відношення сторони до синуса протилежного кута дорівнює діаметру кола, описаного навколо цього трикутника:
2. У трикутнику проти більшої сторони лежить більший кут, проти більшого кута лежить більша сторона. |
|
Годі сперечатися, розкажіть краще, що можна знайти за теоремами |
1)Сторону трикутника за двома його сторонами та кутом між ними; 2)Кути трикутника за трьома його сторонами |
1)Сторону трикутника за однією стороною і прилеглими до неї кутами; 2)Кут трикутника за двома сторонами й кутом, протилежним до однієї з них |
|
Розв’язати трикутник означає – знайти невідомі сторони та кути трикутника за відомими його сторонами і кутами. Наведіть алгоритми розв’язування основних видів задач за теоремами косинусів і синусів |
1. Умова задачі Знайти: АВ, <А,<В
Алгоритм розв’язування
1)
3)<В=180°-<А-ɣ
2. Умова задачі
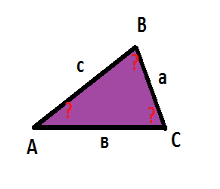
Дано: АС=в, ВС=а, АВ=с Знайти: <А,<В,<С
Алгоритм розв’язування
1)
2) 3)<С=180°- <А - <В.
|
1. Умова задачі Знайти: АС, АВ, <А.
Алгоритм розв’язування
2. Умова задачі
Дано:ВС=а, АС=в, <А=α. Знайти: АВ, <В, <С
Алгоритм розв’язування
1)
2)<С=180° - α- <В;
3)АВ =
|
|
Добре, що обидві командиα оперуєте фактами і можете да вати відсіч одна одній. Наведіть приклади розв’язування задач
VІ. Самостійна робота |
1.Вправа 593 (мал.164)(підручник 9 кл. Бурда М.І., Тарасенкова Н.А.)
2.Вправа 598 (1) 3. Додаткова задача |
1.Вправа 593 (мал.165)
2.Вправа 596 (2) 3. Додаткова задача |
|
VІІ. Підсумок уроку |
Обидві команди показали хорошу гру і знання теорем синусів і косинусів, їх застосування до розв’язування задач. Ви переконались, що конфлікт теорем – надуманий. Кожна із них займає почесне місце в геометрії, зокрема, при розв’язуванні трикутників. На слідуючому уроці ми покажемо застосування даних теорем при розв’язуванні прикладних задач. Надіюсь, що оцінки за самостійну роботу будуть високі. |
|
|
VІІІ. Домашнє завдання |
§ 13. Вправи 595 (1), 597 (2) |
|


про публікацію авторської розробки
Додати розробку

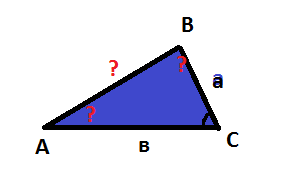 Дано:АС=в, ВС=а,<С=ɣ.
Дано:АС=в, ВС=а,<С=ɣ.
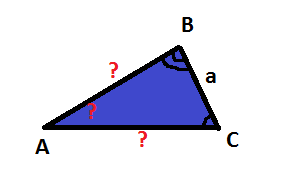 Дано:ВС=а, <В=
Дано:ВС=а, <В=