Урок з геометрії у 9 класі

Тема уроку: Подібність фігур. Площі подібних фігур

Мета уроку: формування поняття подібності фігур;

                      вивчення теореми про площі подібних фігур;

                      формування вмінь застосовувати вивчені означення

                      і властивості до розв’язування задач;

                      формування навичок групової роботи на уроках математики;

    виховання дисциплінованості, логічного мислення, просторової уяви,

    правильно і чітко формулювати означення і теореми.

Тип уроку: комбінований

Обладнання: таблиця, картки із завданнями, підручник з геометрії ав. Бевз В.Г., 

                       креслярське приладдя, мікрофон

Епіграф: «Геометрія є прообразом краси світу»

  Йоганн Кеплер, німецький астроном і математик

Хід уроку

1.Організаційний етап

Перевірити готовність учнів до уроку. Поділ класу на групи.

2.Перевірка домашнього завдання

1) № 489  (0,25)

Експерти в кожній групі перевіряють правильність виконання домашнього завдання

3. Актуалізація опорних знань та вмінь учнів

Інтерактивна вправа «Мікрофон»

• Що таке перетворення подібності?
• Що таке гомотетія? Центр гомотетії ?Коефіцієнт гомотетії?
• Сформулюйте відомі вам властивості перетворення подібності.

4. Мотивація навчальної діяльності учнів

Сьогодні у нас незвичайний урок, на ньому присутні інші вчителі, тому ви повинні бути ще уважнішими і активнішими, злагоджено працюйте в групах і отримаєте гарні оцінки. Епіграфом до уроку я вибрала слова німецького астронома і математика  

Й. Кеплера «Геометрія є прообразом краси світу».

5. Повідомлення теми, мети, завдань уроку

Учні записують в зошити дату, тему уроку.

6. Сприймання і усвідомлення нового матеріалу

Поняття подібності фігур

Фігури F і F₁ називаються подібними, якщо кожній точці фігури F можна поставити у відповідність точку фігури F₁ так, що для довільних точок X і Y фігури F і відповідних точок X₁ і Y₁ фігури F₁ виконується умова, де k – те саме додатне число для всіх точок. При цьому передбачається, що кожна точка фігури F₁ має бути поставлена  у відповідність якій-небудь точці фігури F. Число k називається коефіцієнтом подібності (мал. 174).

 Іншими словами: дві фігури називаються подібними, якщо вони переводяться одна в одну перетворенням подібності. Подібність фігур, як і подібність трикутників, позначають спеціальним знаком: .запис F F₁ читається як «фігура F подібна фігурі F₁».

З означення подібності фігур випливає, що рівні фігури – подібні (k = 1).

Властивості подібних фігур

1. Кожна фігура подібна собі.
2. Якщо фігура F подібна фігурі F₁ з коефіцієнтом подібності k, то фігура F₁ подібна фігурі F з коефіцієнтом 1\k.
3. Якщо фігура F₁ подібна фігурі F₂ з коефіцієнтом подібності k₁, а фігура F₂ подібна фігурі F₃ з коефіцієнтом подібності k₂, то фігура F₁ подібна фігурі F₃ з коефіцієнтом подібності k₁·k₂.
4. Відношення площ подібних фігур дорівнює квадрату коефіцієнта подібності.

S₁\S = k²  .

5. Площі подібних многокутників відносяться як квадрати їхніх відповідних лінійних розмірів.

Розв’язування усних вправ, гра «Мікрофон»

1. Наведіть приклади подібних фігур.
2. Чи подібні будь-які рівні фігури?
3. Чи рівні будь-які подібні фігури? При якій умові подібні фігури рівні?
4. Про дві фігури відомо, що F₂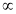F₁ і F₁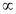F₂  з тим самим коефіцієнтом подібності k. Що можна сказати про значення коефіцієнта k і про фігури

    F₁ і F₂?

5. Згадайте означення подібних трикутників.
6. Сформулюйте ознаки подібності трикутників.

7. Закріплення й осмислення нового матеріалу

Розв’язування задач

1). Сторони двох правильних п - кутників відносяться як а : в. Як відносяться їхні            площі?  (а² : в²)

2). Площі двох квадратів відносяться як 3 : 5. Чому дорівнює сторона меншого квадрата, якщо сторона більшого квадрата дорівнює 10 см?  (см)

3). Площі двох подібних чотирикутників дорівнюють 2 см² і 18 см². Чому дорівнює коефіцієнт подібності?  (к = 3)

4). Периметри подібних многокутників відносяться як 5 : 7, а різниця площ дорівнює 864 см². Знайдіть площі многокутників.  ( 900 см² і 1764 см² )

Самостійна робота в групах

1 група - № 490 (а)  (5)

2 група - № 490 (б)  (16 см²)

Експерти з груп виконують задачу на відкидних дошках, потім учні в своїх групах звіряють правильність розв’язання за записами на відкидних дошках.

Гра «Хто швидше?»

 Задача № 494

Один  учень з кожної групи виконує  завдання біля дошки. Виграє та група представник якої правильно і швидко зробить побудову на дошці.

8. Підбиття підсумків уроку

1). Сформулюйте теорему про відношення площ подібних фігур.

2). Чим запам’ятався цей урок?

3). Оцінювання учнів.

9. Домашнє завдання: § 14, № 491, 501.