Урок з геометрії у 9 класі на тему"Розв’язування трикутників. Прикладні задачі."

Тема: Розв’язування трикутників. Прикладні задачі.

Мета: закріпити, систематизувати і перевірити знання учнів з теми: «Розв’язування трикутників»; вміння та навички знаходження невідомих елементів трикутника за трьома відомими; уміння застосовувати набуті знання до розв’язування трикутників і прикладних задач; поглибити та розширити діапазон знань учнів з теми; 

формувати навички та уміння  практичного  використання набутих теоретичних знань, навчити робити облік  рівня знань  своїх навчальних досягнень, формувати зацікавленість у результатах спільної роботи; розвивати творчі здібності і логічне мислення учнів при знаходженні ними раціональних шляхів для розв’язування практичних задач;

Тип уроку: Урок застосування знань, умінь та навичок учнів.

Форма уроку: Урок - практикум.

Обладнання: картки із завданнями, маршрутні листи, задачі – малюнки, таблиці Брадіса, калькулятори, комп’ютерна презентація, проектор.

Хід уроку

І. Організаційний етап.

Організація уваги учнів. Перевірка готовності классу до заняття.

ІІ. Перевірка домашнього завдання.

Перевіряють учні-асистенти вчителя за зразком на перерві і доповідають про стан виконання домашнього завдання учнями кожної групи.

ІІІ. Оголошення теми та мети уроку.

План уроку записаний у маршрутному листі, який є в кожного на парті. В маршрутному листі є таблиця, в яку кожен учень вписує своє прізвище та ім’я. Також у таблиці записано скількома балами оцінюється завдання кожного етапу уроку.

Учні самостійно занотовують кількість набраних балів за кожен вид роботи.

В кінці уроку учні підсумовують кількість набраних балів і оголошують свої результати.

Маршрутний лист уроку

ІV.  Мотивація навчальної діяльності.

Математика застосовується абсолютно скрізь. Зараз математика застосовується не тільки в астрономії, механіці, фізиці, хімії і техніці, де вона застосовувалася і раніше, але також – у біології, суспільних науках і навіть у мовознавстві. Математики передбачають погоду, обчислюють орбіти штучних супутників, курси кораблів, перекладають наукові тексти з однієї мови на іншу.

Знання стають міцнішими, якщо вони застосовуються у практичній діяльності.

Тому проведемо урок практичного застосування знань, що ви отримали під час вивчення теми «Розв’язування трикутників» і ви дізнаєтеся як можна застосувати знання даної теми в житті.(слайд1)

В давнину за допомогою тригонометрії люди навчилися вимірювати уявні трикутники на небі, вершинами яких були зірки. Зараз тригонометрію застосовують навіть для вимірювання відстані між космічними кораблями.

ІV.  Актуалізація знань, умінь та навичок.

(слайд 2) Епіграфом до нашого уроку буде висловлювання Блеза Паскаля:

«Серед рівних розумом,

за однакових інших умов,

переважає той, хто знає геометрію».

1. Повторення теоретичного матеріалу за допомогою відео «Розв’язування трикутників».

2. Теоретичний бліц-турнір.(слайд 4)

Учитель зачитує запитання, учні відразу відповідають. Неправильні відповіді виправляють самі учні (і лише за необхідності – вчитель). За правильні відповіді учні виставляють у маршрутний лист кількість набраних балів.

Перелік запитань

1.    В чому полягає «розв’язування трикутників»?
2.    Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?
3.    Які теореми потрібно знати, щоб розв’язати трикутник?
4.    Сформулюйте теорему косинусів.
5.    Яку властивість для діагоналей паралелограма можна довести за допомогою теореми косинусів?
6.    Сформулювати теорему синусів.
7.    Сформулювати наслідок з теореми синусів про діаметр кола, описаного навколо трикутника.
8.    Яку властивість бісектриси кута трикутника можна довести за допомогою теореми синусів?
9.    Сформулюйте наслідок про медіани трикутника.
10. Сформулюйте наслідок про співвідношення між кутами трикутника і протилежними сторонами.
11. Сформулюйте теорему про суму кутів трикутника.
12. Скільки типів задач ми розглянули на «розв’язування трикутників»?

3. Математичний диктант. (слайд 5)

1. Запишіть теорему косинусів для сторони а.
2. Запишіть теорему косинусів для сторони в.
3. Запишіть теорему косинусів для сторони с.
4. Виразіть з останньої формули соsγ.
5. Запишіть теорему синусів.
6. Запишіть формулу для обчислення медіани трикутника, проведеної до сторони а.

7)  Запишіть, чому дорівнює квадрат сторони СМ трикутника СDМ.

8) Запишіть рівності, що випливають з теореми синусів для OLK:

9) Який кут трикутника найбільший, якщо його сторони а=7, в=9, с=5?

10) Відомо, що сторона а трикутника менша за кожну з двох інших сторін. Який кут трикутника найменший?

 (Учні, що сидять за однією партою, міняються зошитами та виконують взаємоперевірку.)

4. Метод «Спіймай помилку». (слайд 6)

Неправильно:

1) ;

2)

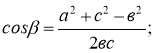
3)

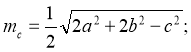
4)

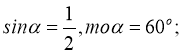
5)

6)

V. Застосування знань, закріплення вмінь і навичок при розв’язуванні задач.

1. Усні вправи. (слайд 7)

Розв’язування задач за готовими малюнками, де потрібно знайти невідомі елементи трикутників за готовими малюнками, які проектуються на екрані.

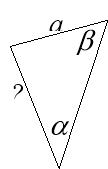
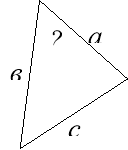
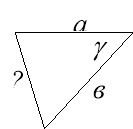
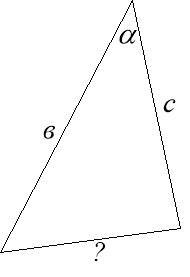
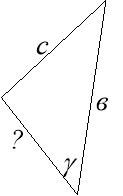
2. Історичні дослідження учнів. (слайд 8)

Теорема Піфагора – перше твердження, яке пов’язувало довжини сторін прямокутного трикутника. Згодом люди дізналися, як вимірювати довжини сторін і величини кутів гострокутного і тупокутного трикутників. Виникла наука «тригонометрія» («тригон» – по грецьки означає «трикутник»). Ця наука широко використовується в життєвих ситуаціях, а саме: для вимірювання висоти предмета, вимірювання відстані до недоступної точки.

Учні заздалегідь готують історичні повідомлення:

1. Причини зародження тригонометрії.  Перші кроки тригонометрії.
2. Вклад вчених в розвиток тригонометрії. Внесок Ейлера в  тригонометрію.

3. Практична геометрія.

Розв’язування задач фронтально, з коментуванням.

№1. (слайд 9)

Знайти відстань від точки А до дерева, яке росте на другому березі річки, якщо з точки А видно це дерево під кутом 40° до лінії берега річки, а з точки В під кутом 50° і відстань між точками А і В дорівнює 20м.

№2. (слайд 10)

 Футбольний м’яч знаходиться в точці А футбольного поля на відстані 23м і 24м від точок В та С відповідно. Футболіст направив м’яч у ворота. Знайдіть кут влучання м’яча у ворота, якщо ширина воріт 7м.

№3. (слайд 11)

Спостерігач знаходиться на відстані 50м від вежі, висоту якої хоче знайти. Основу вежі він бачить під кутом 10° до лінії горизонту, а вершину під кутом 45° до лінії горизонту. Яка висота вежі?

Задача для учнів з високим рівнем знань для самостійного розв’язування.

№4.

На горі побудована вежа, висота якої 100м. Біля підніжжя гори лежить камінь. Цей камінь видно з вершини вежі під кутом 60° до горизонту, а з входу в вежу – під кутом 30° до горизонту. Знайдіть висоту гори.

4. Розв’язування прикладних задач в групах: «Плавання по математичному морю». (слайд 12)

Учні об’єднуються в групи. Кожна група – команда корабля,  під керівництвом свого штурмана - одержує картку із задачею прикладного змісту: необхідно виконати розрахунки і зорієнтуватися, визначити положення корабля в морі. Учні за допомогою вивчених теорем з теми «Розв’язування трикутників» знаходять невідомі відстані і розв’язують дані задачі. Всі члени групи розв’язують задачу в зошиті.

До дошки виходять по одному представнику від кожної групи і пояснюють розв’язок задачі. Учні інших груп записують розв’язок в зошитах.

№1.

Знайти відстань від точки А, в якій знаходиться корабель в певний момент часу до маяка на березі, якщо з цієї точки видно  видно маяк під кутом 60° до курсу , а через деякий час корабель буде знаходитись в точці В –  на відстані 50 км від точки А, і з точки В даний маяк видно під кутом 110° до курсу корабля.

№2.

Берегові радіомаяки А і В розміщені на відстані 10 км один від одного. З  теплоходу С, за допомогою радіолокаційної станції, що знаходиться на ньому. Визначені відстані до маяків СА=11 км і СВ=9км. Знайдіть кути САВ і СВА пеленгів радіомаяків.

VІ. Закріплення знань, умінь і навичок.

Графічний диктант «Так чи ні?» (слайд 13, 14)

Учні креслять трикутник з вершиною вгору, якщо твердження вірне і вершиною вниз, якщо неправильне.

Твердження для диктанту:

1. Теорема синусів справедлива для будь-якого трикутника.
2. 
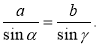
3. За теоремою косинусів можна знайти невідому сторону трикутника, якщо відомі його сторона і два кути.
4. За трьома сторонами можна розв’язати трикутник.
5. с²=а²+в²-2авcos.
6. У трикутнику проти більшого кута лежить менша сторона.
7. За трьома кутами можна розв’язати трикутник.
8. Медіани трикутника діляться точкою їх перетину у відношенні 1:2, починаючи від вершини.
9. Відношення сторони до синуса протилежного кута дорівнює діаметру кола, описаного навколо цього трикутника.
10. Якщо відомо 2 кути трикутника, то третій кут можна знайти за допомогою теореми про суму кутів трикутника.

Ключ до перевірки графічного диктанту проектується на екран.

Кросворд «Розв’язування трикутників» (слайд 15)

По горизонталі:

1.Таблиці Брадіса.

2. Теорема, яка дозволяє знайти квадрат будь-якої сторони трикутника.

3. Чим для теореми синусів є рівність

По вертикалі:

4. Трикутник, у якого один із кутів дорівнює 90^о.

5. Теорема, яка використовується при розв’язуванні трикутників,      якщо відомо один кут і дві сторони, або одна сторона і два кути.

6. Яка сторона лежить у трикутнику проти більшого кута?

7. У трикутнику проти меншого кута лежить менша…?

Відповіді:

По горизонталі:

1. Чотиризначні. 2. Косинусів. 3. Наслідком.

По вертикалі:

4. Прямокутний.5. Синусів. 6.Більша. 7. Сторона.

VІІ. Підсумок уроку.

1. Виставлення і коментування оцінок.

Учні оголошують свої результати.

2. Метод «Чотири ЩО?» (слайд16)

1. Що ви дізналися, навчилися на уроці?
2. Що сподобалося найбільше?
3. Що було найскладнішим?
4. Що треба ще вивчити?

Як ви вважаєте, чи досягли мету уроку?

VІІІ. Домашнє завдання.

Повторити §1. Геометрія 9 клас. А. Г. Мерзляк.

Скласти і розв’язати 1-2 практичні задачі на розв’язування трикутників.

ІХ. Рефлексія.

Метод  «Похвали себе».

Учні вказують на позитивні сторони своєї роботи на уроці.