ВІДКРИТЕ ЗАНЯТТЯ з навчальної дисципліни «Математика» на тему: «Інтеграл та його застосування»

Викладач Тіунова О.І.

Конспект відкритого заняття

Тема    Інтеграл та його застосування Цілі      дидактичні:

§  актуалізувати знання про інтегральне числення;

§  забезпечити узагальнення і систематизацію знань з теми;

§  формувати вміння розв’язувати задачі на обчислення площ плоских фігур, об’ємів тіл обертання, шляху, роботи змінної сили, кількості електрики та об’єму продукції. розвиваючі:

§  розвивати просторову уяву, логічне мислення;

§  розвивати    математичну   мову,       аналітичні       здібності студентів;

§  розвивати мотиваційну сферу особистості;

§  розвивати зацікавленість студентів при розв’язуванні задач прикладного характеру.

виховні:

§  сприяти вихованню наполегливості при розв’язуванні задач;

§  сприяти вихованню культури взаємовідносин при роботі в парах, групах, колективі.

Тип заняття:  узагальнення і систематизація знань

Обладнання: плакати з диференціального та інтегрального числення, таблиця   оцінювання     навчальних досягнень студентів,        емблеми   команд, мультимедійна система.

Роздатковий матеріал:  картки для конкурсу «Перевір себе», картки для конкурсу капітанів.

Очікуванні результати: студенти повинні вміти застосовувати набуті знання при розв’язуванні задач на обчислення площ плоских фігур, об’ємів тіл обертання, шляху, роботи змінної сили, кількості електрики та об’єму продукції.

Структура заняття:

1.  Організаційний момент.

2.  Актуалізація опорних знань, умінь та навичок.

3.  Осмислення знань.

4.  Використання знань при розв’язуванні типових задач.

5.  Підведення підсумків заняття.

6.  Повідомлення домашнього завдання.

«Загублений той час,який ти  не використав на навчання»

Пліній Хід заняття

1. Організаційний момент

В змаганнях приймають участь дві команди: «Диференціал» і «Інтеграл». Викладач представляє капітанів команд та їх учасників, ознайомлює з ходом змагань.

2. Актуалізація опорних знань, умінь та навичок

Оголошуєтьсяконкурс «Відгадай слово»

Командам пропонуються кросворд. Яка з команд першою відгадає зашифроване слово – отримує 2 бали і можливість першою відповідати в наступному конкурсі. 

3. Осмислення знань.

Оголошуєтьсяконкурс «Один за всіх і всі за одного».

Студенти відповідають на запитання викладача (відповіді містять пояснення та обґрунтування). Кожна правильна відповідь оцінюється 1 балом. Якщо ніхто з учасників команди не знає відповіді на запитання, то відповідає команда-суперниця.

Очки нараховуються команді, яка дала правильну відповідь. 

Запитання викладача до команд

1.          Скільки первісних може мати функція, неперервна на відрізку [𝑎𝑎; 𝑏𝑏] ?

2.          Сформулюйте означення невизначеного інтеграла. 

3.          Знайти функцію 𝑦𝑦 = 𝑓𝑓(𝑥𝑥), якщо ∫𝑓𝑓(𝑥𝑥)𝑑𝑑𝑥𝑥 = 𝑥𝑥² + 𝐶𝐶.

4.          Чи можуть графіки первісних однієї функції перетинатися?

5.          Яке рівняння називається диференціальним?

6.          Як можна знайти кількість електрики, що проходить через поперечний переріз провідника за час від 𝑡𝑡₁до 𝑡𝑡₂?

7.          Скільки розв'язків має найпростіше диференціальне рівняння з початковими умовами?

8.          Чи правильно записана формула Ньютона – Лейбніца 

𝑏𝑏

∫_𝑎𝑎 𝑓𝑓(𝑥𝑥)𝑑𝑑𝑥𝑥 = 𝐹𝐹(𝑎𝑎) −𝐹𝐹(𝑏𝑏)?

9.          Сформулюйте геометричний зміст визначеного інтегралу.

10.       Чи правильно записаний механічний зміст визначеного інтеграла 𝑆𝑆 𝑑𝑑𝑡𝑡?

𝑎𝑎

11.       Чому дорівнює визначений інтеграл ∫_𝑎𝑎 𝑓𝑓(𝑥𝑥)𝑑𝑑𝑥𝑥?

12.       Чи залежить визначений інтеграл від позначення змінної інтегрування?

13.       Якщо 𝑝𝑝 = 𝑝𝑝(𝑡𝑡) – продуктивність праці в момент часу t, то як визначити обсяг N випущеної продукції за проміжок часу

[𝑡𝑡₁; 𝑡𝑡₂]? 

14.       Чому дорівнює похідна від невизначеного інтеграла?

15.       Що є розв'язком диференціального рівняння? 

16.       Яка операція називається операцією інтегрування?

17.       Сформулюйте означення первісної функції ?

18.       Що називається інтегральною кривою ?

19.       Який вираз називається підінтегральним ?

20.       Чи вірно, що невизначений інтеграл від довільної степеневої функції знову є степенева функція?

21.       Знайти функцію 𝑦𝑦 = 𝑓𝑓(𝑥𝑥), якщо (∫𝑓𝑓(𝑥𝑥)𝑑𝑑𝑥𝑥)^| = 2^𝑥𝑥.

22.       Що називається частинним розв'язком диференціального рівняння?

23.       Чи правильно записана формула для обчислення об’єму тіла, одержаного обертанням навколо осі абсцис криволінійної трапеції, обмеженої графіком неперервної та невід’ємної

функції 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) на відрізку [𝑎𝑎; 𝑏𝑏] і прямими 𝑥𝑥 = 𝑎𝑎 та 𝑥𝑥 = 𝑏𝑏,𝑉𝑉 =

                        𝑏𝑏 ²(𝑥𝑥)𝑑𝑑𝑥𝑥?

𝜋𝜋∫_𝑎𝑎 𝑓𝑓

24.       Запишіть формулу для знаходження роботи змінної сили 𝐹𝐹(𝑥𝑥)при переміщенні тіла з точки a в точку b.

4. Використання знань при розв’язуванні типових задач.

Оголошуєтьсяконкурс «Перевір себе».

Викладач проводить тестування.

Варіант 1

1.       (1 бал)

2.       (1 бал)

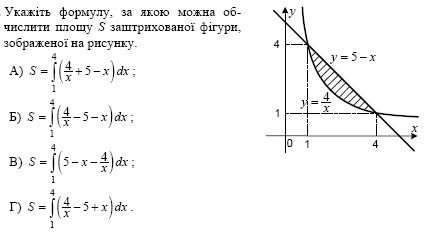
3.       (2 бали)

4.       (2 бали)

Тіло рухається прямолінійно зі швидкістю v(t) = 6−t(м/с). Знайти шлях, пройдений тілом від початку руху до його зупинки.

А)  18 м;        Б)  54 м;        В)  72 м;        Г)  20 м.

5.       (3 бали)

А)  11кв.од.;        Б)  10  кв.од.;        В)  11  кв.од.;        Г)  10  кв.од..

6.       (3 бали)

Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох площі, обмеженої лініями: y x y= ², = 0, x= 2;

А)  5,4𝜋𝜋 куб. од.;        Б)  6,2𝜋𝜋 куб. од.;        В)  6,4𝜋𝜋 куб. од.;        Г) 6,5𝜋𝜋 куб. од..

Варіант 2

1.       (1 бал)

2.       (1 бал)

3.       (2 бали)

4.       (2 бали)

Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох площі, обмеженої лініями: y² =x y, = 0,x= =1,x 2;

А)  1, 4𝜋𝜋 куб. од.;        Б)  1,2𝜋𝜋 куб. од.;        В)  2,4𝜋𝜋 куб. од.;        Г) 1,5𝜋𝜋 куб. од..

5.       (3 бали)

А)  4кв.од.;        Б)  4,5 кв.од.;        В)  4  кв.од.;        Г)  5  кв.од..

6.       (3 бали)

Два тіла почали рухатися одночасно з однієї точки в одному напрямку по прямій. Перше тіло рухається зі швидкістю v₁ = −3t²            t , а друге ^v₂ = −6t        3(м/с). На якій відстані один від одного вони будуть знаходитись через шість секунд.

А)  106 м;        Б)  100 м;        В)  118 м;        Г)  108 м.  

Оголошуєтьсяконкурс капітанів.

Капітани команд біля дошки розв’язують задачі з коментуванням.

Завдання до капітанів команд

Картка 1

1.  (1 бал) Чи є первісними функції 𝐹𝐹₁(𝑥𝑥)і 𝐹𝐹₂(𝑥𝑥)для функції 𝑦𝑦 = 𝑓𝑓(𝑥𝑥)? a)𝐹𝐹₁(𝑥𝑥) = 2^𝑥𝑥 і 𝐹𝐹₂(𝑥𝑥) = 2^𝑥𝑥+4;

b) 𝐹𝐹₁(𝑥𝑥) = 𝑒𝑒^𝑥𝑥 і 𝐹𝐹₂(𝑥𝑥) = 𝑒𝑒^𝑥𝑥 − 8.

Відповідь: а) ні; b) так.

2.  (2 бали) Знайдіть кількість електрики, яка проходить через поперечний переріз провідника за 20с, якщо сила струму змінюється за законом 𝐼𝐼(𝑡𝑡) = 2𝑡𝑡 + 1 (𝐴𝐴).

Відповідь: 420 Кл.

3.  (3 бали) Точка рухається прямолінійно з прискоренням 𝑎𝑎(𝑡𝑡) = 6𝑡𝑡 + 12.  Знайдіть шлях, який пройшла точка за 3с, якщо в момент часу 𝑡𝑡 = 2𝑐𝑐точка мала швидкість 𝑣𝑣 = 38м/ста пройшла шлях 𝑆𝑆 = 30м. Відповідь: 81м.

Картка 2

1.  (1 бал) Які з даних функцій є розв’язками рівняння 𝑥𝑥^′ = 2𝑡𝑡²: 1 ⁴;

a)   𝑥𝑥 =𝑡𝑡

2

2³;

b)   𝑥𝑥 =𝑡𝑡

3

2³ + 5?

c)   𝑥𝑥 =𝑡𝑡 3

Відповідь: а) ні; b) так; с) так.

2.  (2 бали) Визначити, яку кількість продукції виготовлено за 8 годин, якщо продуктивність праці визначається функцією

𝑝𝑝(𝑡𝑡) = −3𝑡𝑡² + 10𝑡𝑡 + 75. Відповідь: 408 од.

3.  (3 бали) Обчислити роботу, яку треба затратити для стискання пружини на 4 см, якщо для стискання її на 1 см потрібна сила 10Н. Відповідь: 0,8 Дж.

Оголошуєтьсяконкурс «Магічний квадрат».

Студенти у своїх командах знаходять числа «магічного квадрату». За кожне правильно знайдене число команда отримує 1 бал.

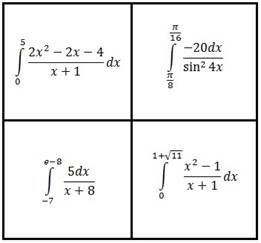 Відповідь:   

5.  Підведення підсумків заняття.

Викладач оголошує переможця змагань, оцінює роботу студентів на занятті. Оцінювання навчальних досягнень студентів проводиться за таблицею

6.  Повідомлення домашнього завдання

За підручником [1] розв’язати задачі № 6, 7, 9, 10 c. 215 – 216.

Література

1.  Нелін Є. П., Долгова О. Є. Алгебра і початки аналізу: Дворівневий підруч. для 11 кл. загальноосвіт. навч. закладів.— 2-ге вид., виправл. і доп.— Х.: Світ дитинства, 2006. – 416 с. 

2.  Роєва Т.Г., Хроленко Н.Ф. Алгебра у таблицях. 11 клас: Навч. посібник. – Х.: Видавнича група «Академія», 2001. – 130с. 

3.  Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика. 11 клас: Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. –Тернопіль: Навчальна книга – Богдан, 2011. — 480 с.

4.  Роєва Т.Г., Адруг Л.М. Алгебра і початки аналізу. Завдання для тематичного оцінювання. 10, 11 кл. – К.: Країна мрій, 2007. – 178с.

5.  Математика: Комплексна підготовка до зовнішнього незалежного оцінювання / Уклад.: А. М. Капіносов, Г. І. Білоусова, Г. В. Гап’юк, Л. І. Кондратьєва, О. М. Мартинюк, С. В. Мартишок, Л. І. Олійник, П. І. Ульшин, О. Й. Чиж. — Тернопіль : Підручники і посібники, 2013. — 528 с.

6.  Збірник завдань для державної підсумкової атестації з математики: 11-й кл.: у 2-х ч./ А.Г. Мерзляк [та ін. ]; за ред. М.І. Бурди. . – К.: Центр навч.-метод. л-ри, 2014. – 224 с.

7.  Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підруч. для 10 – 11 кл. загальноосвіт. навч. закладів.      

- 2-ге вид. – К.: Зодіак – ЕКО, 2002. – 656 с.

Додаток №1

Варіант 1

1.       (1 бал)

2.       (1 бал)

3.       (2 бали)

4.       (2 бали)

Тіло рухається прямолінійно зі швидкістю v(t) = 6−t (м/с). Знайти шлях, пройдений тілом від початку руху до його зупинки.

А)  18 м;        Б)  54 м;        В)  72 м;        Г)  20 м.

5.       (3 бали)

А)  11кв.од.;        Б)  10  кв.од.;        В)  11  кв.од.;        Г)  10  кв.од..

6.       (3 бали)

Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох площі, обмеженої лініями: y x y= ², = 0, x= 2;

А)  5,4𝜋𝜋 куб. од.;        Б)  6,2𝜋𝜋 куб. од.;        В)  6,4𝜋𝜋 куб. од.;        Г) 6,5𝜋𝜋 куб. од..

Варіант 2

1.       (1 бал)

2.       (1 бал)

3.       (2 бали)

4.       (2 бали)

Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох площі, обмеженої лініями: y² =x y, = 0,x= =1,x 2;

А)  1, 4𝜋𝜋 куб. од.;        Б)  1,2𝜋𝜋 куб. од.;        В)  2,4𝜋𝜋 куб. од.;        Г) 1,5𝜋𝜋 куб. од.

5.       (3 бали)

А)  4кв.од.;        Б)  4,5 кв.од.;        В)  4  кв.од.;        Г)  5  кв.од..

6.       (3 бали)

Два тіла почали рухатися одночасно з однієї точки в одному напрямку по прямій. Перше тіло рухається зі швидкістю v₁ = −3t²            t , а друге ^v₂ = −6t        3(м/с). На якій відстані один від одного вони будуть знаходитись через шість секунд.

А)  106 м;        Б)  100 м;        В)  118 м;        Г)  108 м.

Додаток №2

Відповіді до тестів

Переведення оцінки в балах в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів

        Сума балів, нарахованих за виконані студентом завдання, переводиться в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів за спеціальною шкалою.

        Максимально можлива сума балів за тестування становить 12 (див. табл. 1). Відповідність кількості набраних студентом балів оцінці за 12-бальною системою оцінювання навчальних досягнень студентів наведено в таблиці 2.

Таблиця 1

Таблиця 2

Додаток №3

Завдання до капітанів команд

Картка 1

1.  (1 бал) Чи є первісними функції 𝐹𝐹₁(𝑥𝑥)і 𝐹𝐹₂(𝑥𝑥)для функції 𝑦𝑦 = 𝑓𝑓(𝑥𝑥)? a)𝐹𝐹₁(𝑥𝑥) = 2^𝑥𝑥 і 𝐹𝐹₂(𝑥𝑥) = 2^𝑥𝑥+4;

b) 𝐹𝐹₁(𝑥𝑥) = 𝑒𝑒^𝑥𝑥 і 𝐹𝐹₂(𝑥𝑥) = 𝑒𝑒^𝑥𝑥 − 8. 

2.  (2 бали) Знайдіть кількість електрики, яка проходить через поперечний переріз провідника за 20с, якщо сила струму змінюється за законом 𝐼𝐼(𝑡𝑡) = 2𝑡𝑡 + 1 (𝐴𝐴).

3.  (3 бали) Точка рухається прямолінійно з прискоренням 𝑎𝑎(𝑡𝑡) = 6𝑡𝑡 + 12.  Знайдіть шлях, який пройшла точка за 3с, якщо в момент часу 𝑡𝑡 = 2𝑐𝑐точка мала швидкість 𝑣𝑣 = 38м/ста пройшла шлях 𝑆𝑆 = 30м.

Картка 2

1.  (1 бал) Які з даних функцій є розв’язками рівняння 𝑥𝑥^′ = 2𝑡𝑡²: 1 ⁴;

a)   𝑥𝑥 =𝑡𝑡 2

2³;

b)   𝑥𝑥 =𝑡𝑡

3

2³ + 5?

c)   𝑥𝑥 =𝑡𝑡 3

2.  (2 бали) Визначити, яку кількість продукції виготовлено за 8 годин, якщо продуктивність праці визначається функцією

𝑝𝑝(𝑡𝑡) = −3𝑡𝑡² + 10𝑡𝑡 + 75.

3.  (3 бали) Обчислити роботу, яку треба затратити для стискання пружини на 4 см, якщо для стискання її на 1 см потрібна сила 10Н.