Урок з математики на тему: «Об’єми тіл обертання та площі їх поверхонь»
ВІДКРИТЕ ЗАНЯТТЯ з навчальної дисципліни «Математика» на тему: «Об’єми тіл обертання та площі їх поверхонь»
Викладач Тіунова О.І.
Конспект відкритого заняття
![]()
Тема Об’єми тіл обертання та площі їх поверхонь Цілі дидактичні:
• актуалізувати знання про тіла обертання;
• забезпечити узагальнення і систематизацію знань з теми;
• формувати вміння розв’язувати задачі на знаходження об’ємів тіл обертання та площ їх поверхонь. розвиваючі:
• розвивати просторову уяву, логічне мислення;
• розвивати математичну мову, аналітичні здібності студентів;
• розвивати мотиваційну сферу особистості;
• розвивати зацікавленість студентів при розв’язуванні задач прикладного характеру.
виховні:
• сприяти вихованню наполегливості при розв’язуванні задач;
• сприяти вихованню культури взаємовідносин при роботі в парах, групах, колективі.
Тип заняття: узагальнення і систематизація знань
Обладнання: моделі і плакати стереометричних фігур, таблиця оцінювання навчальних досягнень студентів, емблеми команд, мультимедійна система.
Роздатковий матеріал: картки для конкурсу «Перевір себе», картки для конкурсу капітанів, картки для конкурсу «Один за всіх і всі за одного».
Очікуванні результати: студенти повинні вміти застосовувати набуті знання при розв’язуванні задач на знаходження об’ємів тіл обертання та площ їх поверхонь.
Структура заняття:
1. Організаційний момент.
2. Актуалізація опорних знань, умінь та навичок.
3. Осмислення знань.
4. Використання знань при розв’язуванні типових задач.
5. Підведення підсумків заняття.
6. Повідомлення домашнього завдання.
Теорія без практики мертва і безплідна, практика без теорії неможлива
Рене Декарт Хід заняття
1. Організаційний момент
Привітання команд, підготовка їх до змагань. 2. Актуалізація опорних знань, умінь та навичок
Оголошуєтьсяконкурс презентацій
В змаганнях приймають участь три команди: «Циліндр», «Конус», «Куля». Кожна команда готувала теоретичний матеріал (презентацію, питання), практичний матеріал (3 задачі) своїм опонентам відповідно до своєї назви.
Презентація команди «Циліндр» План.
1. Поняття циліндра та його властивості.
2. Перерізи циліндра площинами.
3. Вписана і описана призми, дотична площина до циліндра.
4. Об’єм та площа поверхні циліндра.
5. Циліндр в нашому житті.
6. Тренувальні вправи.
Презентація команди «Конус» План.
1. Поняття конуса та його властивості.
2. Перерізи конуса площинами.
3. Поняття зрізаного конуса та його властивості.
4. Вписана і описана піраміди, дотична площина до конуса.
5. Об’єм та площа поверхні конуса, зрізаного конуса.
6. Конус в нашому житті.
7. Тренувальні вправи.
Презентація команди «Куля» План.
1. Поняття кулі та її властивості.
2. Перерізи кулі площинами.
3. Поняття частин кулі.
4. Комбінації кулі з іншими тілами, дотична площина до кулі.
5. Об’єм та площа поверхні кулі та її частин.
6. Куля в нашому житті.
7. Тренувальні вправи.
3. Осмислення знань.
Оголошуєтьсяконкурс «Мозковий штурм».
Студенти відповідають на питання своїх опонентів та викладача (відповіді містять пояснення та обґрунтування).
Питання команди «Циліндр»
1. Чи можна торт, який має форму прямого кругового циліндра, розрізати на вісім частин трьома перерізами? (Так)
2. Чи рівні об’єми тіл, утворених при перетині прямого кругового циліндра площиною, що проходить через його вісь? (Так)
3. Чи правильно, що рівновеликі циліндри рівні між собою? (Ні)
4. Чи правильно, що площа поверхні прямого кругового циліндра не зміниться, якщо радіус основи збільшити вдвічі, а висоту зменшити вдвічі? (Ні)
Питання команди «Конус»
1. Чи мають рівновеликі конуси з рівновеликими основами рівні висоти? (Так)
2. Чи зміниться об’єм прямого кругового конуса, якщо радіус основи конуса зменшити вдвічі, а висоту збільшити вдвічі? (Так. Зменшиться вдвічі)
3. Чи правильно, що відрізок, який з’єднує вершину кругового конуса з центром його основи, є висотою конуса? (Ні)
4. Чи може висота конуса мати з ним лише одну спільну точку?
(Так)
Питання команди «Куля»
1. Чи можуть кулі з рівними площами поверхонь мати різні об’єми? (Ні)
2. Чи рівні між собою дві рівновеликі кулі? (Так)
3. Чи може перерізом сфери радіуса R бути коло радіуса 1,1 R? (Ні) 4. Чи може фігура обертання мати тільки одну площину симетрії?
(Ні)
Питання викладача до команд
1. Два перерізи сфери мають однакову довжину. Чи правильно, що січні площини рівновіддалені від центра сфери? Відповідь: так.
2. Як виражається об’єм прямого кругового циліндра через площу бічної поверхні і радіус основи?
1
Відповідь:V=2![]() 𝑆𝑆б𝑅𝑅
𝑆𝑆б𝑅𝑅
3. Нехай рівновеликі прямі кругові конуси мають рівні площі основ. Чи рівновеликі їхні осьові перерізи?
Відповідь:так.
4. Використання знань при розв’язуванні типових задач.
Оголошуєтьсяконкурс «Перевір себе».
Викладач проводить тестування.
Варіант 1
1. (0,5∙4 = 2 бали)

2. (2 бали)

3. (2 бали)

4. (2 бали)

5. (4 бали)

Варіант 2
1. (0,5∙4 = 2 бали)

2. (2 бали)

3. (2 бали)

4. (2 бали)

5. (4 бали)
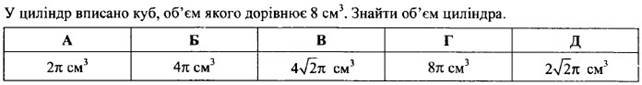
Оголошуєтьсяконкурс капітанів.
Капітани команд біля дошки розв’язують задачі з коментуванням.
Завдання до капітанів команд
1. Площа бічної поверхні циліндра дорівнює половині площі його повної поверхні. Діагональ осьового перерізу дорівнює 5 см. Знайти повну поверхню циліндра.
Відповідь: 20𝜋𝜋 см2.
2. Знайдіть площу бічної поверхні, повної поверхні та об’єм прямого кругового зрізаного конуса за його осьовим перерізом, зображеним на рис.1.
4

14
Рис.1
Відповідь: 117πкв. од.; 170π кв. од.; 268 πкуб. од.
3. Радіуси основ кульового пояса дорівнюють 10 см і 12 см, а його висота – 11 см. Знайдіть бічну поверхню кульового пояса, якщо паралельні площини, які перетинають кулю, розміщені з різних боків від центра кулі. Відповідь: 275𝜋𝜋 см2
Оголошуєтьсяконкурс «Один за всіх і всі за одного».
Студенти у своїх командах розв’язують задачі, підготовлені опонентами. Кожна команда розв’язує 3 задачі і записує розв’язання на дошці з коментуванням.
Задачі команди «Циліндр»
1. Стіжок сіна має форму циліндра. Радіус його основи 3м, висота – 4м. Густина сіна 0,03 г/см3. Визначити масу стіжка сіна. Відповідь: ≈ 3,4 т
2. Паралельно осі циліндра проведено переріз, який є квадратом зі стороною 6см і відтинає від кола основи дугу, градусна міра якої дорівнює 900. Знайдіть площу бічної поверхні циліндра. Відповідь: ![]() 𝜋𝜋 см2
𝜋𝜋 см2
3. У нижній основі циліндра проведено хорду, яку видно з центра цієї основи під кутом β. Відрізок, що сполучає центр верхньої основи із серединою цієї хорди, дорівнює l і утворює з площиною основи кут α. Знайдіть об’єм циліндра.
𝜋𝜋𝑙𝑙3sin𝛼𝛼cos2𝛼𝛼
Відповідь: 2𝛽𝛽 куб.од.
cos ![]()
2
Задачі команди «Конус»
1. Площа бічної поверхні конуса дорівнює 240π см2. Знайдіть об’єм цього конуса, якщо радіус його основи дорівнює 12 см.
Відповідь: 960𝜋𝜋 см3
2. Скільки жерсті витрачено на виготовлення 10 відер, висота кожного з яких дорівнює 42 см, а діаметри основ – 28 см і 34 см? (На шви і відходи йде 12% матеріалу).
Відповідь: ≈ 528 дм2
3. Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, який утворює з площиною основи конуса кут β. Знайдіть площу бічної поверхні конуса, якщо його висота дорівнює Н.
𝜋𝜋𝐻𝐻21−𝑠𝑠𝑠𝑠𝑠𝑠2𝛽𝛽𝑐𝑐𝑐𝑐𝑠𝑠2𝛼𝛼
2
![]() Відповідь: 𝑠𝑠𝑠𝑠𝑠𝑠2𝛽𝛽𝑐𝑐𝑐𝑐𝑠𝑠2𝛼𝛼 кв.од.
Відповідь: 𝑠𝑠𝑠𝑠𝑠𝑠2𝛽𝛽𝑐𝑐𝑐𝑐𝑠𝑠2𝛼𝛼 кв.од.
2
Задачі команди «Куля»
1. У кулі на відстані 12 см від її центра проведено переріз, площа якого дорівнює 81π см2. Знайдіть об’єм кулі.
Відповідь: 4500𝜋𝜋 см3
2. Довжина лінії перетину сфери і площини дорівнює 10π см, а радіус сфери, проведений в одну з точок лінії перетину, утворює з площиною перетину кут 60°. Знайдіть площу поверхні сфери.
Відповідь: 400𝜋𝜋 см2
3. Зовнішній діаметр порожнистої кулі 18 см. Товщина стінок 3 см. Знайдіть об’єм матеріалу, з якого виготовлено кулю. Відповідь: 684𝜋𝜋 см3
5. Підведення підсумків заняття.
Викладач оголошує переможця змагань, оцінює роботу студентів на занятті. Оцінювання навчальних досягнень студентів проводиться за таблицею
|
|
Учасники команд |
|
|
|
|
|
|
|
|
|
1. Деркач Г.О. |
|
|
|
|
|
|
|
|
2. Кравченко Т.В. |
|
|
|
|
|
|
|
|
|
3. Вітусевич Є.С. |
|
|
|
|
|
|
|
|
|
4. Путін О.Г. |
|
|
|
|
|
|
|
|
|
5. Зайцев Ю.В. |
|
|
|
|
|
|
|
|
|
6. Єфименко В.С. |
|
|
|
|
|
|
|
|
|
7. Литвин В.М. |
|
|
|
|
|
|
|
|
|
8. Тригуб В.Ю. |
|
|
|
|
|
|
|
|
|
9. Чернов Л.О. |
|
|
|
|
|
|
|
|
|
10. Шевцов О.О. |
|
|
|
|
|
|
|
|
|
Загальний бал |
|
|
|
|
|
|
|
|
|
|
1. Тисячний В.В. |
|
|
|
|
|
|
|
|
2. Дума І.С. |
|
|
|
|
|
|
|
|
|
3. Жуков О.В. |
|
|
|
|
|
|
|
|
|
4. Сьомін Д.А. |
|
|
|
|
|
|
|
|
|
5. Зубчик А.О. |
|
|
|
|
|
|
|
|
|
6. Бойко С.М. |
|
|
|
|
|
|
|
|
|
7. Васильченко Є.А. |
|
|
|
|
|
|
|
|
|
8. Немець Є.Р. |
|
|
|
|
|
|
|
|
|
9. Кривошлик Н.М. |
|
|
|
|
|
|
|
|
|
Загальний бал |
|
|
|
|
|
|
|
|
|
|
1. Нужненко Я.О. |
|
|
|
|
|
|
|
|
2. Ландига Я.І. |
|
|
|
|
|
|
|
|
|
3. Губський М.М. |
|
|
|
|
|
|
|
|
|
4. Мурзін О.О. |
|
|
|
|
|
|
|
|
|
5. Коблай А.С. |
|
|
|
|
|
|
|
|
|
6. Бойченко Є.В. |
|
|
|
|
|
|
|
|
|
7. Кулешов В.О. |
|
|
|
|
|
|
|
|
|
8. Кокоша Р.С. |
|
|
|
|
|
|
|
|
|
9. Терніцький П.В. |
|
|
|
|
|
|
|
|
|
Загальний бал |
|
|
|
|
|
|
|
|
6. Повідомлення домашнього завдання
За підручником [3] розв’язати задачі № 338, 343, 350, c. 394 – 396.
Література
1. Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 10-11 кл. загальноосвіт. навч. закл.– К.: Школяр, 2004. – 256 с.
2. Роєва Т.Г., Хроленко Н.Ф., Геометрія у таблицях. 10 – 11 класи: Навч. посібник. – Х.: Видавнича група «Академія», 2001. – 152с.
3. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика. 11 клас: Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. –Тернопіль: Навчальна книга – Богдан, 2011. — 480 с.
4. Роєва Т.Г., Адруг Л.М. Геометрія. Завдання для тематичного оцінювання. 10, 11 кл. – К.: Країна мрій, 2007. – 178с.
5. Математика: Комплексна підготовка до зовнішнього незалежного оцінювання / Уклад.: А. М. Капіносов, Г. І. Білоусова, Г. В. Гап’юк, Л. І. Кондратьєва, О. М. Мартинюк, С. В. Мартишок,Л. І. Олійник, П. І. Ульшин, О. Й. Чиж. — Тернопіль : Підручники і посібники, 2013. — 528 с.
6. Збірник завдань для державної підсумкової атестації з математики: 11-й кл.: у 2-х ч./ А.Г. Мерзляк [та ін. ]; за ред. М.І. Бурди. . – К.: Центр навч.-метод. л-ри, 2014. – 224 с.
Додаток №1
Варіант 1
1. (0,5![]() 4 = 2 бали)
4 = 2 бали)

2.

3.

4.

5.

Варіант 2
1.

2.

3.

4.

5.
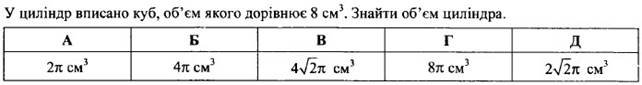
Додаток №2
Відповіді до тестів
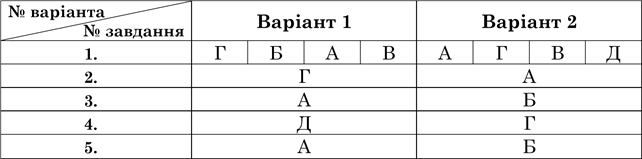
Переведення оцінки в балах в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів
Сума балів, нарахованих за виконані студентом завдання, переводиться в оцінку за 12-бальною системою оцінювання навчальних досягнень студентів за спеціальною шкалою.
Максимально можлива сума балів за тестування становить 12 (див. табл. 1). Відповідність кількості набраних студентом балів оцінці за 12-бальною системою оцінювання навчальних досягнень студентів наведено в таблиці 2.
Таблиця 1
|
Номери завдань |
Кількість балів |
Усього |
|
1 – 4 |
по 2 бали |
8 балів |
|
5 |
4 бали |
4 бали |
|
Сума балів |
12 балів |
|
Таблиця 2
|
Кількість набраних балів |
Оцінка за 12-бальною системою оцінювання навчальних досягнень студентів |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
8 |
|
9 |
9 |
|
10 |
10 |
|
11 |
11 |
|
12 |
12 |
Задачі команди «Циліндр»
1. Стіжок сіна має форму циліндра. Радіус його основи 3м, висота – 4м. Густина сіна 0,03 г/см3. Визначити масу стіжка сіна.
2. Паралельно осі циліндра проведено переріз, який є квадратом зі стороною 6см і відтинає від кола основи дугу, градусна міра якої дорівнює 900. Знайдіть площу бічної поверхні циліндра.
3. У нижній основі циліндра проведено хорду, яку видно з центра цієї основи під кутом β. Відрізок, що сполучає центр верхньої основи із серединою цієї хорди, дорівнює l і утворює з площиною основи кут α. Знайдіть об’єм циліндра.
![]()
Задачі команди «Конус»
1. Площа бічної поверхні конуса дорівнює 240π см2. Знайдіть об’єм цього конуса, якщо радіус його основи дорівнює 12 см.
2. Скільки жерсті витрачено на виготовлення 10 відер, висота кожного з яких дорівнює 42 см, а діаметри основ – 28 см і 34 см? (На шви і відходи йде 12% матеріалу).
3. Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, який утворює з площиною основи конуса кут β. Знайдіть площу бічної поверхні конуса, якщо його висота дорівнює Н.
![]()
Задачі команди «Куля»
1. У кулі на відстані 12 см від її центра проведено переріз, площа якого дорівнює 81π см2. Знайдіть об’єм кулі.
2. Довжина лінії перетину сфери і площини дорівнює 10π см, а радіус сфери, проведений в одну з точок лінії перетину, утворює з площиною перетину кут 60°. Знайдіть площу поверхні сфери.
3. Зовнішній діаметр порожнистої кулі 18 см. Товщина стінок 3 см. Знайдіть об’єм матеріалу, з якого виготовлено кулю.
Додаток №4
Завдання до капітанів команд
1. Площа бічної поверхні циліндра дорівнює половині площі його повної поверхні. Діагональ осьового перерізу дорівнює 5 см. Знайти повну поверхню циліндра.
2. Знайдіть площу бічної поверхні, повної поверхні та об’єм прямого кругового зрізаного конуса за його осьовим перерізом, зображеним на рис.1.
4

14
Рис.1
3. Радіуси основ кульового пояса дорівнюють 10 см і 12 см, а його висота – 11 см. Знайдіть бічну поверхню кульового пояса, якщо паралельні площини, які перетинають кулю, розміщені з різних боків від центра кулі.


про публікацію авторської розробки
Додати розробку