Урок з підприємницьким тлом на тему: "Застосування властивостей геометричних тіл до моделювання реальних процесів"

ВСП РОМЕНСЬКИЙ ФАХОВИЙ КОЛЕДЖ КНЕУ

НАВЧАЛЬНО-МЕТОДИЧНА КАРТКА (ПЛАН) ЗАНЯТТЯ № 25

Предмет            Математика                Група  Н-2-1           Дата  03.11.2022          

Тема заняття: Застосування властивостей геометричних тіл до моделювання реальних процесів

Вид заняття:   узагальнення та систематизація знань

Тип уроку: урок з підприємницьким тлом

Мета заняття

Навчальна: узагальнити та систематизувати  знання про розгортки, площі поверхонь циліндра, конуса, зрізаного конуса, кулі та сфери а також уміння та навички знаходити площі поверхонь тіл обертання; створити умови для усвідомлення цінності практичного використання вказаних умінь та навичок. Розвиваюча: розвивати вміння створювати математичну модель прикладної задачі, уміння студентів робити порівняльний аналіз,розвивати ініціативність, лідерські якості, комунікативні вміння, розвивати вміння концентрувати увагу, узагальнювати і систематизувати, проводити аналогію, працездатність, логічне мислення Виховна: виховувати зацікавленість дисципліною, прагнення отримувати нові знання самостійно та вміти використовувати їх на практиці.

Забезпечення заняття

А. Наочність: моделі тіл обертання, мультимедійна презентація. Б. Роздатковий матеріал: опорний конспект, схематичне креслення виробу, креслярські інструменти. картки самооцінювання роботи в групі В. ТЗН: мультимедійний комплекс Г. Література: Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: підруч. для 11 кл. загальноосвіт. навчальн. закладів: академ. рівень, профільн. рівень - Вид. 3-гє – К.: Генеза, 2014.- 336 с.

 

Методи і техніки:

• «кейс-метод» (ситуаційні вправи);
• робота в малих группах.

 

Операційні цілі (завдання):

Після закінчення заняття студент знає

• розгортки тіл обертання, формули для обчислення площ поверхонь тіл обертання, розрізняє тіла обертання;

розуміє

• цінність практичного використання вказаних формул, значення математики для ведення успішної підприємницької діяльності;

вміє

• знаходити площі поверхонь тіл обертання та розв’язувати прикладні задачі на обчислення площ поверхонь тіл обертання;

може

•    аналізувати проблемну ситуацію;
•    шукати оптимальні шляхи вирішення проблеми;
•    планувати діяльність;
•    генерувати пропозиції та робити висновки;
•    виявляти ініціативу і вміння вести дискусію;
•    здійснювати градацію цінностей;
•    виявляти ініціативу;
•    наводити аргументи та відстоювати власну позицію;
•    приймати миттєві рішення при зміні умов завдання;
•    співпрацювати в команді.

 

Хід заняття:

1.  Організаційна частина заняття.

Активізація уваги; створення робочої атмосфери для проведення заняття. Група ділиться на три малих групи.

2. Мотивація студентів до навчання

Моделюємо проблемну ситуацію:

До нас, як до знавців властивостей тіл обертання, звернувся один з вітчизняних фермерів-початківців, який після відповідного оформлення землі (близько 30 га) вирішив обрати в якості особистого бізнесу вирощування зерна.  Він розуміє, що, маючи можливість протримати зерно в доброму стані до весни, можна значно збільшити свій прибуток.  У той же час усвідомлює, що за відсутності потрібної господарської інфраструктури це практично неможливо.  Двір біля садиби малий, надпольний склад не побудуєш, тому прийняв рішення побудувати зерносховище баштового типу, або, як його ще називають, - силос.  Цей фермер звернувся з проханням обчислити розхід матеріалів та їхню вартість для монтажу каркасу зерносховища з оцинкованого металу.

 

 

3. Повідомлення теми, мети та основних завдань заняття

Отже, щоб виправдати його сподівання і правильно розв’язати поставлену задачу, нам необхідно повторити, узагальнити і систематизувати наші знання про тіла обертання.

 

4. Актуалізація раніше засвоєних знань.
   • Фронтальне розв’язування кросворду «Тіла обертання» (додаток 1).

5. Узагальнення та систематизація теоретичних знань.
   • Вправа «Установи відповідність, щоб дізнатися девіз заняття»

 

 

 

Девіз заняття:

 

• Вправа «Питання-відповідь»

 

Циліндр

1. Що являє собою розгортка бічної поверхні циліндра?
2. Що називається твірною циліндра?
3. Взаємне розміщення осі циліндра з твірними.
4. Яку фігуру треба обертати і навколо чого, щоб утворився циліндр?
5. Яка фігура утворюється в осьовому перерізі циліндра, якщо діаметр основи рівний висоті циліндра?

Конус

1. Яку фігуру треба обертати і навколо чого, щоб утворився конус?
2. Який конус називається рівностороннім?
3. Яка фігура утворюється в осьовому перерізі зрізаного конуса?
4. Що являє собою розгортка бічної поверхні конуса?
5. Висота конуса це - …

 

Куля

1. Яка фігура називається кулею?
2. Яка січна площина має найбільшу площу?
3. Яким є взаємне розміщення дотичної до кулі площини і радіусом кулі, проведеним в точку дотику?
4. Як називається відрізок, який сполучає дві точки кульової поверхні і проходить через центр?

Як називається частина кулі, яку відтинає від неї січна площина?

• Гра «Вірю – не вірю»

 

• Вправа «Знайди помилку»

 

 

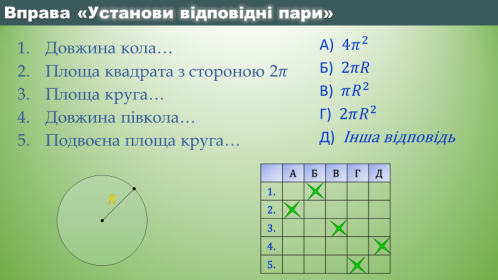
• Вправа «Установи відповідні пари»

 

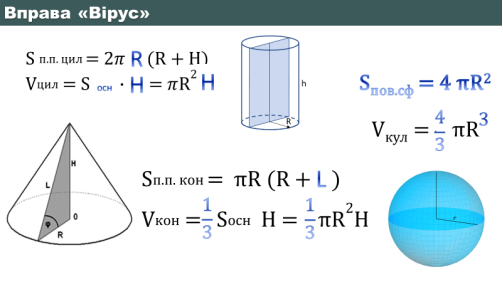
• Вправа «Вірус»

6. Розв’язування задач в стандартних умовах

7. Розв’язування задач в нестандартних умовах
   • Розв’язування ситуаційної кейс-вправи в малих групах.

 

                 Пропонуємо студентам в групах проаналізувати ситуацію, провести математичне моделювання ситуації та скласти наближений план дій для обчислення площ поверхонь  тіл обертання, спираючись на їх власний досвід і отримані знання та вміння. Дати відповідь на питання: які виміри необхідно для цього виконати. Націлюємо студентів на те, що вони у малих групах цілком самостійно мають розв’язати цю задачу, дійти висновку: які вхідні дані їм необхідні, які знання необхідні.

 Під час обговорення тільки спостерігаємо за ходом та виконанням правил ведення дискусії. Після обговорення кожна група надає слово своєму представнику для оголошення результатів.

Переходимо до вироблення спільного плану дій, повідомляємо про свої враження від активності та креативності мислення студентів, їх уміння давати пропозиції, планувати діяльність, робити висновки.

Роздаємо групам опорні конспекти (додаток 2).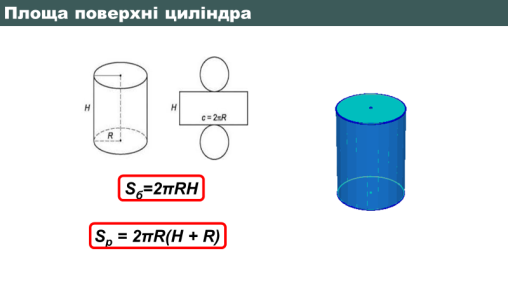

 

Пропонуємо самостійно ознайомитися з теоретичним матеріалом опорного конспекту. Через декілька хвилин запитуємо у студентів які поняття чи визначення залишилися їм незрозумілі. Пояснюємо їх. Важливо запитати, наскільки прочитане збігається з їхніми висновками про спосіб вирішення задачі.

 

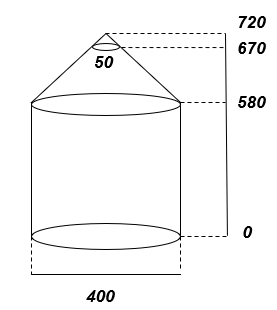
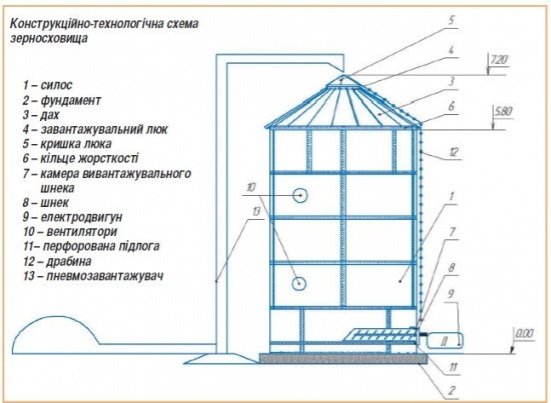
Визначаємося, яка з груп розрахує відповідну частину каркасу (стіни - циліндр, дах – зрізаний конус та люк – конус). Роздаємо схематичне креслення виробу (додаток 3) та відповідні моделі геометричних тіл.

 

Формулюємо математичну умову кожної задачі. Повідомляємо студентів, що вони можуть розпочинати вирішувати проблемну задачу, користуючись схемою й отриманими матеріалами.

 

 

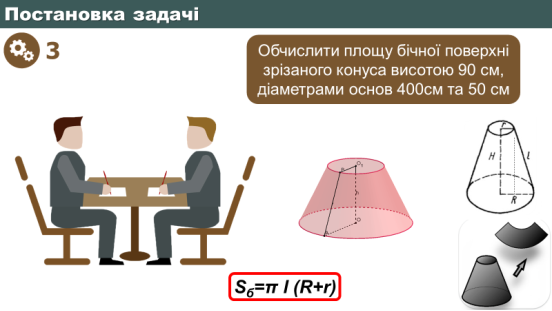
Вислуховуємо презентацію груп щодо виконаної роботи. Заохочуємо інших студентів висловлювати власну думку щодо коректності знайдених результатів. Особливо уважно розбираємо помилкові обчислення, просимо студентів пояснити, як вони мислили. Упевнюємося, що студенти усвідомили помилку.

 

 

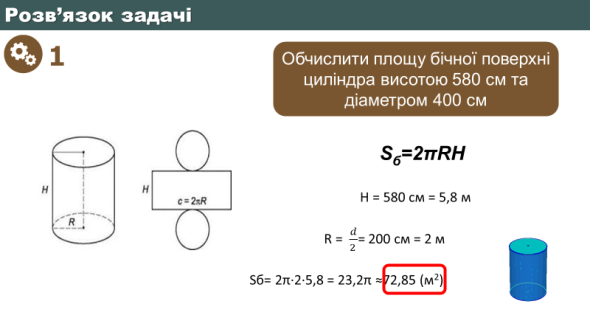
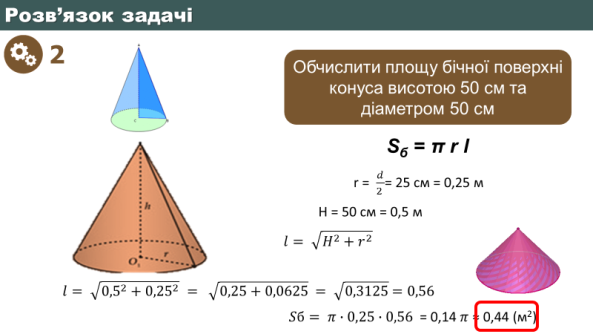
Разом обчислюємо загальну площу поверхні отриманого комбінованого тіла обертання.

 

 

8. Підсумки.

Підводимо підсумки про спосіб обчислення площ поверхонь  тіл обертання, наголошуємо на важливості теми у повсякденному житті на прикладі вирішеної задачі, даємо усну оцінку самостійній роботі студентів, підкреслюємо виявлену креативність, творчість, організованість під час роботи в групі. Заповнюємо картки самооцінювання роботи в групі (додаток 4)  та виставляємо оцінки

 

 

 

9. Домашнє завдання.
   1. Знайдіть необхідну кількість листів оцинкованого металу товщиною 3 мм, враховуючи найраціональніший спосіб розкрою матеріалу та її вартість за найвигіднішими цінами в інтернет пропозиціях.
   2. Виясніть: можливо вигідніше виготовити ємність такого ж об’єму у формі прямокутного паралелепіпеда з діагоналлю квадрата в основі, що дорівнює основі циліндра і дахом у вигляді чотирикутної піраміди

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

Кроссворд «Тіла обертання»

 

					1
								2		3
					4								5
			6
										7
		8
	9				10
				11

ПО ГОРИЗОНТАЛІ

4.Відрізок, що з'єднує центр кола (сфери) з довільною точкою цього кола (сфери).7.Відстань від основи предмета до найвіддаленішої його точки вгорі по вертикальній лінії.8.Тіло, яке складається з двох кругів, що лежать у різних площинах та суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки даних кругів.9.Тіло обертання, яке виходить в результаті обертання прямокутного трикутника навколо його катета.11.Будь-який переріз кулі площиною є ...

ПО ВЕРТИКАЛІ

1.Відрізок, що сполучає вершину конуса з точкою границі його основи.2.Найдовша хорда.3.Переріз тіла обертання, що проходить через його вісь.5.Геометричне місце точок площини, відстань від яких до заданої точки, що називається центром кола, є постійною величиною і дорівнює радіусу кола.6.Площина, що проходить через твірну циліндра і перпендикулярна площині осьового перерізу, що містить цю площину.9.Множина всіх точок простору, що перебувають від заданої точки O на відстані, не більшій за дану відстань R.10.Поверхня кулі.

Відповіді до кросворду:

 

1 т

в

і

2 д

3 о

4 р

а

д

і

у

с

5 к

н

а

ь

о

6 д

а

м

о

л

о

е

7 в

и

с

о

т

а

т

т

и

8 ц

и

л

і

н

д

р

й

ч

9 к

о

н

у

10 с

у

а

ф

л

е

я

11 к

р

у

г

а

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2

Опорний конспект

ЦИЛIНДР

Прямим циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.

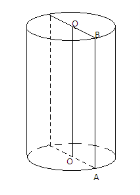Якщо прямокутник обертається навколо осі , його сторони описують рівні круги, які лежать у паралельних площинах. Ці круги називають основами циліндра.

Радіус циліндра - це радіус його основи.

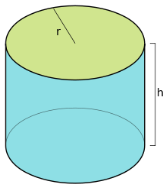Сторона АВ паралельна осі циліндра описує криву поверхню, яку називають бічною поверхнею циліндра. Твірною циліндра називаються відрізки, які лежать на бічній поверхні і сполучають відповідні точки кіл основ. Вони паралельні і рівні.

Усі твірні одного циліндра рівні і паралельні одна одній. Довжина твірної - висота циліндра – це відстань між площинами його основ.

Віссю циліндра називається пряма, яка проходить через центри основ. Вісь циліндра паралельна твірним. Усі осьові перерізи циліндра – рівні прямокутники.

 

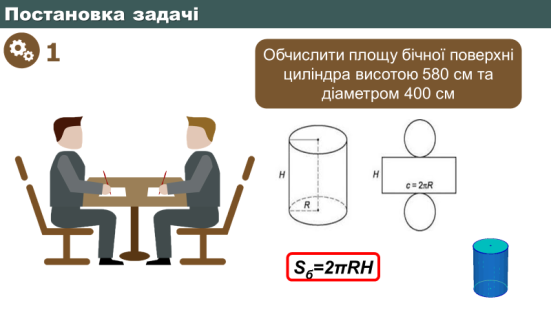
Розгортка циліндра – це прямокутник з висотою H і довжиною 2πR та два круга радіусом R , отже, площа бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за формулою:

 

S_б=2πRH

 

 

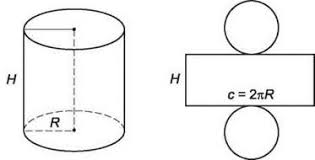
Площа повної поверхні циліндра складається з площ основ та площі бічної поверхні і дорівнює:

S_p = 2πR(Н + R).

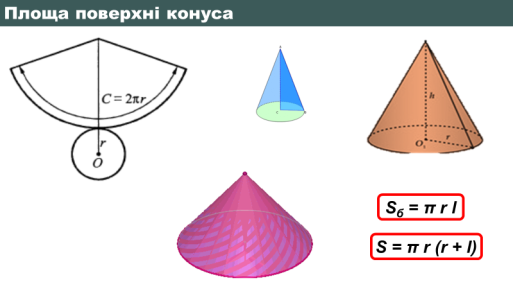
КОНУС.

Конусом називається геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску поверхню.

Прямим круговим конусом називається тіло, утворене обертанням прямокутного трикутника навколо його катета.

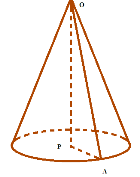Якщо прямокутний трикутник ОРА обертати навколо катета РО, його гіпотенуза РА опише бічну поверхню, а катет ОА круг – основу конуса. Радіус цього круга називають радіусом конуса.

Висота конуса – це перпендикуляр, опущений із його вершини на площину основи.

Відрізок, що сполучає вершину конуса з будь-якою точкою кола його основи, називається твірною конуса. Множина всіх твірних конуса утворює бічну поверхню конуса.

Усі осьові перерізи конуса – рівні рівнобедрені трикутники.

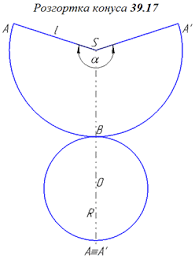
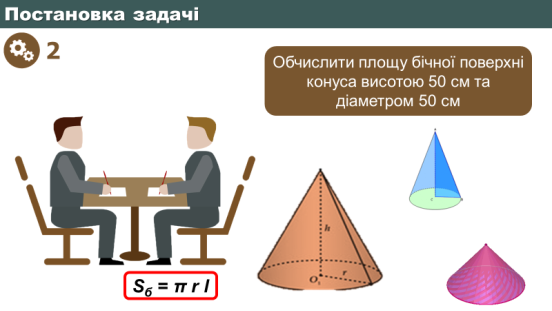
Площа бічної поверхні конуса радіуса та з твірною дорівнює  S_б = πrl

Площа повної поверхні конуса дорівнює       S = πr(r + l)        .

 

 

 

 

 

 

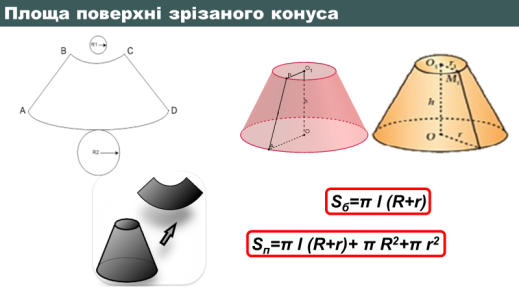
ЗРIЗАНИЙ КОНУС

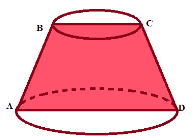Якщо конус перетнути площиною, паралельною основі конуса, площина перетинатиме конус по кругу і відітне від конуса менший конус. Частина, що залишилась, називається зрізаним конусом.

Зрізаним конусом називається тіло утворене обертанням прямокутної трапеції навколо меншої її бічної сторони. Осьовим перерізом зрізаного конуса є рівнобічна трапеція, в якої основи - діаметри основ зрізаного конуса, бічні сторони - твірні, висота - висота зрізаного конуса.

 

 

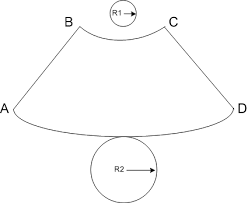
Площа бічної поверхні зрізаного конуса:

S_б=πl(R+r)

 

Площа повної поверхні зрізаного конуса:

S_п=πl(R+r)+ πR²+πr²

де R і r – радіуси основ зрізаного конуса, l – твірна зрізаного конуса.

 

 

 

 

 

 

 

КУЛЯ ТА СФЕРА

Кулею називається тіло утворене обертанням круга навколо його діаметра.

Сферою називається фігура, утворена обертанням кола навколо його діаметра.

Будь-який відрізок, що сполучає центр кулі з якою-небудь точкою його поверхні називається радіусом кулі.

Відрізок, який сполучає дві точки поверхні кулі та проходить через центр, називається діаметром кулі.

Будь-який переріз кулі площиною є круг. Центр цього круга є основою перпендикуляра, опущеного з центра кулі на січну площину.

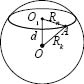На малюнку - радіус кулі,

                     - радіус перерізу,

                     - відстань від центра кулі до площини перерізу (d).

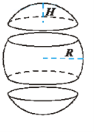Площина яка проходить через діаметр кулі – діаметральна площина. Вона розбиває кулю на дві рівні півкулі. Переріз кулі діаметральною площиною називається великим кругом, а переріз сфери .- великим колом, або екватором.

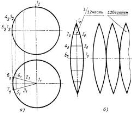
Площа сфери радіуса дорівнює         .

Частина кулі, яку відтинає площина називається кульовим сегментом. Його поверхня складається зі сферичного сегмента і круга – основи кульового сегмента.

Частина кулі, яка міститься між двома паралельними січними площинами називається кульовим шаром. Поверхня кульового шару називається кульовим поясом.

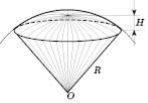Тіло, утворене обертанням опуклого кругового сектора навколо радіуса, що обмежує його, називається кульовим сектором.

Кульовий сектор - це кульовий сегмент і конус, вершина якого в центрі кулі, а основою є основа сегмента.

Додаток 3

 

СХЕМАТИЧНЕ КРЕСЛЕННЯ ВИРОБУ

 

 

 

 

 

 

 

 

 

Додаток 4

 

Самооцінювання роботи в групі

 

Дата _______________

Прізвище, ім’я студента _____________________________________________

Покладіть собі від 0 до 2 балів за кожне запитання:

1. Ви брали активну участь у роботі групи ______________________________

2. Ви вносили вдалі пропозиції, які врахувала група ______________________

3. Ви надавали підтримку іншим членам групи, заохочували їх до роботи ___

4. Ви висунули цілком нову ідею, що сподобалась іншим _________________

5. Ви вдало узагальнювали думки інших і просували роботу групи вперед ___

6. Ви брали участь у представлені результатів ___________________________

Всього балів _______________

Підпис групи

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використані інформаційні джерела.

 

 

1. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: підруч. для 11 кл. загальноосвіт. навчальн. закладів: академ. рівень, профільн. рівень - Вид. 3-гє – К.: Генеза, 2014.- 336 с
2. Шкільна академія підприємництва 3 [Електронний ресурс]/ – Режим доступу: http://sae-ukraine.org.ua/ua//
3. Лекция 11-12 кейс-метод, кейс технология [Електронний ресурс]/НФПК – Режим доступу: http://www.openclass.ru/node/284481.
4. Вказівки до підготовки завдань за кейс-методом [Електронний ресурс]/ ПЕДКАБІНЕТ блог для викладачів СТБО – Режим доступу: https://pedkab.wordpress.com
5. Доклад по математике «Применение кейс-технологий на уроках математики» [Електронний ресурс]/ VIDEOUROKI – Режим доступу: http://videouroki.net/filecom.php?fileid=98697337
6. Case – технологии на уроках математики [Електронний ресурс]/ Фестиваль педагогических идей «Открытый урок» – Режим доступу: http://festival.1september.ru/articles/593299/
7. Кросворд «Тіла обертання»  [Електронний ресурс]/ Кросворди з математики – Режим доступу: https://onlinetestpad.com/ua/crossword/17090-t%D1%96la-obertannya
8. Немецкий опыт построения зернохранилища руками украинского фермера [Електронний ресурс]/©Пропозиція - Главный журнал по вопросам агробизнеса – Режим доступу:
   http://propozitsiya.com/nemeckiy-opyt-postroeniya-zernohranilishcha-rukami-ukrainskogo-fermera