Урок з теми: "Числові множини"

       Числа — це боги.  

  Платон

       Число висвітлює глибину світобудови.  

Г. Лейбніц

Тема уроку: Числові множини. (Раціональні числа. Ірраціональні та дійсні числа. Числові множини. Етапи розвитку поняття числа.)

Мета уроку.

Навчальна: формування поняття числової множини, вмінь і знань відшукувати  і розрізняти  раціональні, ірраціональні, дійсні, натуральні та цілі числа та користуватися їх ознаками.

Розвиваюча: інтелектуальний розвиток учнів, розвиток логічного мислення, пам’яті, уваги, інтуїції, уміння аналізувати, робити умовиводи за аналогією.

Виховна: виховання акуратності записів, чіткості й точності думки, працелюбства, наполегливості, алгоритмічної культури.

Тип уроку: Урок засвоєння нових знань.

Методи і прийоми: метод «Акваріум», гра «Сигнал», гра «Весела лічба», гра «Хто швидше».

Підручник: Алгебра 8, А.Г. Мерзляк, В.Б.Полонський, М.С.Якір

Хід уроку

І. Актуалізація опорних знань.

Учні витягують назву групи. Це може бути «Натуральні числа», «Цілі числа», «Раціональні числа».

Вчитель. Будемо працювати методом «Акваріум». Перша група «Натуральні числа» займає центральний стіл, а один представник отримує завдання.

1. Які числа називаються натуральними?
2. Яке найменше натуральне число?
3. Яке найбільше натуральне число?
4. Скільки є натуральних чисел?
5. Які дії виконують з натуральними числами?

 2 хвилини обговорюють, 1 хвилина  на озвучення відповідей , 1 хвилина для зовнішнього кола на  обговорення правильності даних відповідей.

Друга група «Цілі числа» займає центральний стіл. Отримує завдання:

1.Які числа називаються цілими?

2. Яких чисел більше цілих чи натуральних? Чому?

3. Які практичні потреби привели до необхідності в цілих числах?

4. Чи буде сума, різниця, добуток  і частка двох цілих чисел цілим числом?

2 хвилини обговорюють, 1 хвилина  на озвучення відповідей , 1 хвилина для зовнішнього кола на обговорення правильності даних відповідей.

Третя група «Раціональні числа» займає центральний стіл. Отримує завдання:

1.Які числа називаються раціональними?

2. Чи можна сказати, що число 0 є натуральним, цілим і раціональним?

3. Чи можна сказати, що число  5 є натуральним, цілим і раціональним?

4. Чи можна сказати, що число - 5 є натуральним, цілим і раціональним?

5. Чи можна сказати, що число  є натуральним, цілим і раціональним?

2 хвилини обговорюють, 1 хвилина  на озвучення відповідей , 1 хвилина для зовнішнього кола на  обговорення правильності даних відповідей.

ІІ. Мотивація. Ще Й. В. Гете сказав «Цифри не керують світом, але вони показують, як світом керувати». Сьогодні ми продовжимо працювати із числами, які утворюються за допомогою цифр. Без них сьогодні неможливо уявити життя людей. Спочатку для підрахунку певних предметів навколишнього світу утворилися натуральні числа. Згодом натуральних чисел людям  виявилося замало для того, що виражати   для прикладу  розміри своїх скарбів і боргів, температури повітря і т.д.   Отже, появилися цілі числа. Та і тут людству стало зрозуміло, що не все можна виразити цілим числом потрібні нові числа. Ними виявилися раціональні. Кожен день із збільшеннями потреб людства, вдосконаленням виробництва виникали потреби і в числам. Чи можете ви сьогодні уявити хоча б день, коли б  ви не використовували чисел?

ІІІ. Тема, мета і основні завдання уроку.

 Сьогодні на уроці ми з вами розглянемо  відомі на сьогоднішній день множини чисел і спробуємо дати влучні їм характеристики. Отже, запишіть тему уроку « Числові множини».

IV. Сприймання і усвідомлення учнями нового матеріалу

Ви ще в 5 класі ознайомилися з множиною натуральних чисел, яку ми надалі будемо позначати буквою N. Сьогодні ми сказали, що найменшим натуральним числом є 1, 0 не належить множині натуральних чисел, найбільшого числа не існує. Згодом із збільшенням потреб людства виникли від’ємні числа.  Тому натуральні числа, протилежні їм і число 0 стали утворювати множину цілих чисел, яку позначають буквою Z. Отже бачимо, що множина натуральних чисел є підмножиною цілих чисел, тобто N Z .

Згодом людям стало зрозуміло, що деякі об’єкти навколишнього світу не можуть бути виражені цілими числами. Появилися дроби і разо з ними поняття раціональних чисел. Отже раціональні числа – це цілі і дробові( додатні і від’ємні). Їх позначають буквою Q.Бачимо з означення раціональних чисел, що N Z  Q. Тобто натуральні і цілі числа є підмножиною раціональних. Ще в 6 класі ми подавали раціональні числа у вигляді , де m – ціле число,n – натуральне. Наприклад, 7=

Раціональне число можна подати у вигляді скінченого десяткового дробу , як наприклад або нескінченого періодичного десяткового дробу, як , Цифра 3, яка  повторюється є періодом дробу. 3=3,(0)..,4 =4,(0).

Отже кожне раціональне число можна подати у вигляді нескінченного десяткового  періодичного дробу. І кожен нескінчений періодичний дріб є записом деякого раціонального числа.

Давайте з’ясуємо, яким числом є:

• сума натуральних чисел;
• добуток натуральних чисел
• різниця натуральних чисел;
• частка натуральних чисел

Учні аналізують. Роблять висновки. У деяких випадках вчитель наводить контраргументи.

Дріб може бути скінченим

Вам додому давалося завдання на випередження. Отже, як називаються числа, які не є раціональними? Наведіть приклади ірраціональних чисел.

Яку множину утворюють раціональні і ірраціональні числа?

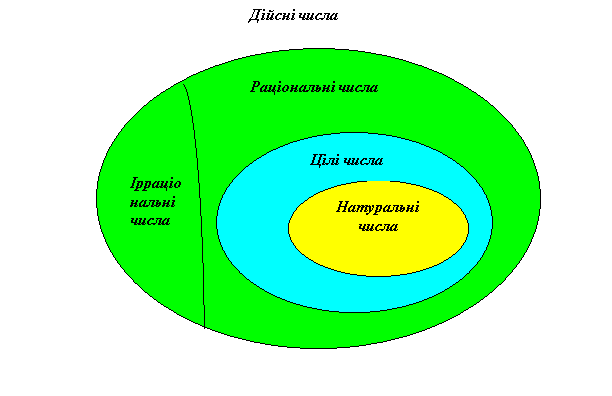
Так, це множина дійсних чисел, яка позначається буквою R  і містить множини натуральних, цілих, раціональних чисел, тобто N Z  Q R.

Тобто справедливі слова С. Отевіна: «Серед чисел існує досконалість і згода.»  

V. Осмислення знань.

Вчитель. Г. Лейбніц сказав: «Не будемо сперечатись, обчислимо істину.» Отже вирахуйте істиними чи хибними є твердження з  №426, №427, №428, №429

Гра «Сигнал» Піднімаємо зелену карточку, якщо твердження істинне  і  червону, якщо твердження хибне.

Усно з аргументованими поясненнями №446, №444,№440.

Письмово №448,№453,№455,458.

VІ. Узагальнення системи знань.

І.При вивченні натуральних чисел ми вивчали подільність їх на 2, 5,10,3,9. Зараз пограємо гру «Весела лічба»(2-3 учні).

Назвати підряд всі числа від 1 до 40. Але замість тих чисел, що діляться на 3 або в записі мають трійку, говорити своє ім'я. Хто зіб'ється — з гри вибуває.

ІІ. Гра «Хто швидше». За 1 хвилину потрібно дати найбільше відповідей.

1. Чому дорівнює добуток всіх цифр?

2. Скільки буде десятків, коли три десятки помножити на два десятки?

3. Що більше: сума всіх одноцифрових чисел чи їх добуток?

4. На яке найбільше число ділиться без остачі будь- яке дане число?

5. На яке найменше число ділиться без остачі на будь-яке дане число?

6. Яке найбільше число можна записати за допомогою трьох одиниць?

7.  Які числа називаються дійсними?

8.  Скільки у будь-якому числі цифр після цифр сотень?

9. Які числа називаються натуральними?

10. Яке натуральне число дорівнює числу букв в його назві?

 11. Назвіть два числа, де кількість цифр дорівнює кількості букв, з яких складаються назви цих чисел. 

12. Чому дорівнює сума всіх цифр.

13. Скільки разів трапляється десятицифрове число, коли лічиш від 1 до 1000 000 000? 

14.Які числа називаються цілими?

15. Зліва від знака дорівнює постав дужки, щоб утворена рівність, була правильною.

4 х 12 +  18 : 6 + 3 = 50 

VІІ. Підсумок уроку.

Вчитель. Сьогодні на уроці ми ознайомилися з числовим множинами.

Сподіваюсь розумієте, що будь-які математичні відкриття робилися на основі практичних потреб людства. А зараз оцініть свою роботу на уроці?

VІІІ. Домашнє завдання.

Вивчити п 14, виконати №№449, №454, №456