Урок з теми: "Графічний спосіб розв’язування систем лінійних рівнянь"
![]()
![]()

Цілі:
навчальна: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язування систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (x; y) розв’язком даної системи, розв’язувати систему двох лінійних рівнянь графічним способом.
розвивальна: формувати вміння самостійно здобувати знання, працювати з текстом підручника;
виховна: виховувати позитивне ставлення до знань.
Тип уроку: формування компетентностей
Обладнання: роздавальний матеріал, комп’ютер.
Хід уроку.
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
Виконую перевірку домашнього завдання, використовуючи комп’ютер.
ІІІ. Актуалізація опорних знань.
Математична естафета (на комп’ютерах – тестер „BDV–test”)
Учні з кожного ряду сідають по черзі до комп’ютера і розв’язують вправи. Перемагає команда, яка першою розв’яже всі завдання (враховується швидкість і якість – результати записані на комп’ютері)
Завдання тесту
Варіант І
- Лінійним рівнянням з двома змінними називається...
А Рівняння виду ax+by=c, де a, b, c – змінні, x і y – числа;
Б Рівняння виду ax+by=c, де a, b, c – дані числа, x і y – змінні;
В Рівняння виду ax–by=c, де a, b, c – дані числа, x і y – змінні;
Г Рівняння виду ax+by+c, де a, b, c – дані числа, x і y – змінні;
- Графіком рівняння ax+by=c, якщо b=0, є...
А Пряма, що збігається з віссю Oy; Б Пряма, паралельна осі Ox; В Пряма, паралельна осі ординат;
Г Пряма, перпендикулярна до осі ординат
- Кожній точці координатної площини відповідає...
А Точка; Б Пара чисел;
В Пара точок; Г Число
- Графіком рівняння ax+by=c, якщо a=0, є...
А Пряма, що збігається з віссю Ox ; Б Пряма, паралельна осі Oy; В Пряма, паралельна осі абсцис; Г Точка
- Кожна точка графіка рівняння з двома змінними має такі координати, що...
А Задовольняють дане рівняння; Б Задають точку площини; В Задовольняють рівність; Г Є коренем рівняння
- Два рівняння з двома змінними називають рівносильними, якщо...
А Кожне з них має безліч розв’язків;
Б Вони відрізняються лише вільним членом; В Вони однакові;
Г Кожне з них має ті самі розв’язки, що й інше, або рівняння, які не мають роз’язків
Варіант ІІ
- Рівнянням першого степеня з двома змінними називається...
А Лінійне рівняння з двома змінними x і y, в якому a0 і b0;
Б Лінійне рівняння з двома змінними x і y, в якому a0;
В Рівняння з двома змінними x і y, в якому a0 і b0;
Г Лінійне рівняння з двома змінними x і y, в якому b0;
- Розв’язком рівняння з двома змінними називається...
А Корінь рівняння з двома змінними;
Б Число, яке задовольняє рівняння з двома змінними;
В Пара чисел, яка задовольняє рівняння з двома змінними;
Г Будь-яка пара чисел
- Графіком рівняння 0x+0y=0 є...
А Крива; Б Пряма, паралельна осі ординат;
В Вся координатна площина; Г Пряма, перпендикулярна до осі абсцис
- Кожній парі чисел на координатній площині відповідає...
А Єдина точка; Б Пара точок;
В Пряма; Г Крива
- Графіком кожного рівняння першого степеня з двома змінними є...
А Пара прямих; Б Пара точок;
В Крива; Г Пряма
- Скільки розв’язків має рівняння першого степеня з двома змінними?
А Безліч розв’язків; Б Два розв’язки;
В Безліч коренів Г Один розв’язок
ІV. Вивчення нового матеріалу.
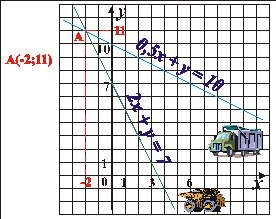 Уявімо, що графік – це маршрут автомобіля. Візьмемо маршрути двох автомобілів із домашнього завдання (2x+y=7 і 0,5x+y=10) і накладемо їх один на один. Що відбулося? (Графіки перетнулися)
Уявімо, що графік – це маршрут автомобіля. Візьмемо маршрути двох автомобілів із домашнього завдання (2x+y=7 і 0,5x+y=10) і накладемо їх один на один. Що відбулося? (Графіки перетнулися)
Визначте місце зустрічі автомобілів: точку перетину графіків лінійних рівнянь з двома змінними. Чим є координати цієї точки для даних лінійних рівнянь з двома змінними? (Координати точки є для них спільним розв’язком)
Отже, ми знайшли спільний розв’язок двох лінійних рівнянь з двома змінними – точку перетину графіків рівнянь. Якщо потрібно знайти спільні розв’язки двох і більше рівнянь, то говорять, що ці рівняння утворюють систему. Тобто ми можемо зробити висновок, що система – це декілька рівнянь, для яких потрібно знайти спільний розв’язок.
Що є розв’язком системи рівнянь з двома змінними? Це пара значень змінних, що перетворює кожне рівняння системи у правильну рівність, тобто є спільним розв’язком усіх рівнянь системи.
Виконаємо усно декілька вправ (Робота з картками)
Завдання
- яка з пар (1; 1), (–1; –1), (0,5; 2), (–0,5;–2) є розв’язком системи рівнянь:
![]()
![]() а) x+y= –2, б) xy= 1,
а) x+y= –2, б) xy= 1,
3x–2y= –1; 2x–y= 1?
- знайдіть підбором два розв’язки системи рівнянь:
![]()
![]() а) m+n=7, б) m+n=11,
а) m+n=7, б) m+n=11,
mn=12; mn=10.
Так от сьогодні ми і повинні навчитися розв’язувати системи рівнянь з двома змінними. Розглянемо один із способів розв’язування – графічний.
Складемо алгоритм розв’язування систем рівнянь графічним способом. (спочатку усно). Правильність складеного алгоритму перевіряємо по карткам в конверті, що лежить на кожному ряді.
Алгоритм розв’язування систем рівнянь графічним способом
- Побудувати графіки кожного з рівнянь в одній системі координат.
- Знайти координати точки перетину прямих, якщо вона є.
- Записати відповідь.
Розбираємо приклад розв’язування системи рівнянь, використовуючи даний алгоритм (записи на моніторах комп’ютера)
Приклад.
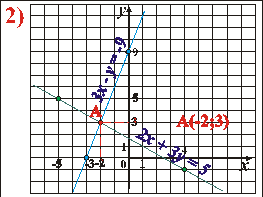 Розв’язати систему рівнянь:
Розв’язати систему рівнянь: 
- Будуємо графіки кожного з рівнянь в одній системі координат.
1–й графік: 2x+3y=5
|
x |
–5 |
4 |
|
y |
5 |
–1 |
2–й графік: 3x–y=–9
|
x |
–3 |
0 |
|
y |
0 |
9 |
- Знаходимо координати точки перетину прямих: A(–2; 3)
- Відповідь: (–2; 3)
А чи завжди система лінійних рівнянь з двома змінними має один розв’язок? Ось тут нам і потрібно згадати взаємне розташування графіків двох лінійних рівнянь a1x+b1y=c1 і a2x+b2y=c2.
 Тепер ми можемо дати відповідь на питання:
Тепер ми можемо дати відповідь на питання:
- Скільки розв’язків може мати система лінійних рівнянь з двома змінними? (один, безліч, жодного)
- В яких випадках система має один розв’язок (безліч, немає)?
Системи рівнянь можуть мати безліч розв’язків, якщо графіки цих рівнянь є одна й та сама пряма. Системи рівнянь можуть не мати жодного розв’язку, якщо графіки цих рівнянь – паралельні прямі. Отже:
- Робота з картками:
-
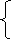
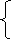 чи має система рівнянь розв’язок:
чи має система рівнянь розв’язок:
а) 2x+3y=7, б) 3x+4y= –2,
x–y=6; 9x+12y=11?
- при якому значенні с система має безліч розв’язків:
![]()
![]() а) 3x–y=10, б) 1/2x+1/5y=c,
а) 3x–y=10, б) 1/2x+1/5y=c,
9x–3y=c; 5x+2y=3?
V. Розв’язування вправ.
Розв’язати системи рівнянь, які задані на картках, графічним способом.
Завдання на картках
|
1.
4. |
Чотири системи з шести запропонованих на картках розв’язують по одному учню. Решту систем учні розв’язують самостійно. Розв’язування перевіряємо за допомогою комп’ютера.
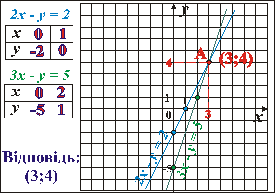
1. 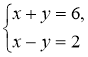 Відповідь: (4; 2) 2.
Відповідь: (4; 2) 2. 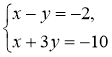 Відповідь: (–4; -2)
Відповідь: (–4; -2)
3. 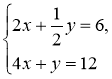 Відповідь: безліч 4.
Відповідь: безліч 4. 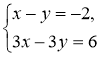 Відповідь:
Відповідь:
 5.
5. 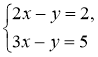 6.
6. 

Після цього звертаємось до шифрограми, записаної на дошці.
|
А |
Л |
К |
О |
Т |
У |
Д |
Р |
Е |
И |
|
|
(2; 8) |
безліч |
(1;2) |
(–3; 2) |
(–3; 3) |
(4; 2) |
(3; 4) |
(–4; –2) |
(–1; 7) |
Відповідь: Декарт.
VІ. Історична довідка.
Рене Декарт – французький математик, філософ, фізик, який першим почав використовувати координати точок. Тому їх часто називають декартовими координатами, а систему координат, у якій ми будували графіки, декартовою системою координат. Дворянин за походженням, народився 1596 року. Він не відразу знайшов своє місце в житті. Після закінчення коледжу у 1612 р. Спочатку готувався до військової кар’єри, пізніше поринув у світське життя, подорожував країнами Європи, потім все кинув заради науки.
Декарт намагався і в філософії і в будь-якій іншій науці знайти математичні закони, звести кожне питання або кожну задачу до математичної.
У 1637 р. Вийшла книжка „Міркування про метод”, у якій поряд із загальним філософським міркуванням про матерію значну увагу приділено „універсальній математиці”. В одному з розділів автор запропонував новий метод – метод координат, який дав можливість переходити від точки (у координатній площині) до пари чисел, від лінії до рівняння, від геометрії до алгебри. Це була нова геометрія, яку зараз називають аналітичною геометрією.
Заслуга Р.Декарта полягає також у тому, що він увів позначення, які збереглися до нашого часу: латинські букви x, y, z – для змінних; a, b, c – для коефіцієнтів. Завдяки цьому кожній прямій у координатній площині відповідає лінійне рівняння ax+by=c (де a або b відмінні від нуля числа) і навпаки.
Метод координат дає змогу будувати графіки рівнянь, зображати геометрично залежності, виражені за допомогою рівнянь і формул, розв’язувати геометричні задачі за допомогою алгебри.
З іменем Декарта ми будемо зустрічатися, вивчаючи механіку, оптику, біологію. З 1628 р. Декарт жив у Голландії, у 1619 р. Переїхав у Швецію, де і помер від пневмонії у 1650 р.
VІІ. Домашнє завдання (проектор, на початку уроку)
§ 4 п.26, пит.1–6 № 1008, 1011, 987, 1002 (ст.194) [1]
ІX. Підсумок уроку.
Рефлексія
Учитель:
- Чи складною була тема? Що здалося найлегшим?
- В аркуші самооцінювання виставте собі оцінку за:
|
Листок самооцінювання Прізвище, ім’я______________________________________ а) розуміння навчального матеріалу (1–3 бали)___________; б) кількість і якість розв’язаних вправ (1–3 бали)_________; в) активність на уроці, висунення ідей, що привели до розв’язання поставлених завдань (1–3 бали)___________________________________; г) самостійність (1–3 бали)____________________________
|
Ряд, який працював найкраще, отримує додатковий бал.


про публікацію авторської розробки
Додати розробку
