Урок з теми "Обчислення задач на знаходження площі поверхні многогранників"

Тема уроку:   

Розв’язування задач

на обчислення площі поверхні многогранників

Мета уроку:

• дидактична: повторити, систематизувати, узагальнити знання учнів про многогранники, площу бічної поверхні многогранників, площу повної поверхні многогранників;
• розвиваюча: розвивати в учнів сприйняття геометричних фігур, логічне мислення, процеси аналізу і синтезу;
• виховна: виховувати математичну культуру, наполегливість і почуття своєї вагомості в колективі, любов до математики

Обладнання: мультимедійний проектор, дошка

Тип уроку: закріплення вивченого матеріалу

Методи і прийоми: «Робота в малих групах», гра «Хрестики-нолики»,  «Мікрофон»

Очікувані результати:  після уроку учні зможуть:

• дати означення:

•            многогранник;
•            піраміда;
•            призма;
•            паралелепіпед;
•            елементи многогранників

• розв’язувати задачі на знаходження площі бічної та повної поверхні многогранників.

Хід уроку

І Організаційний момент (3 хв.)

Вступне слово.  

- Добрий день. Сідайте, будь ласка. Поки ви готуєтесь до уроку, налаштовуєтесь на роботу, я відмічу відсутніх. Чергові будь ласка, перевірте готовність дошки до роботи.

- Тема нашого уроку «Розв’язування задач на обчислення площі поверхні многогранників». Мета уроку: навчитися застосовувати набуті знання при розв’язуванні різних задач.

Після уроку ви зможете:

• дати означення:

•            многогранник;
•            піраміда;
•            призма;
•            паралелепіпед;
•            елементи многогранників

• розв’язувати задачі на знаходження площі бічної та повної поверхні многогранників.

- І першим етапом уроку буде перевірки домашнього завдання.

ІІ Перевірка домашнього завдання (7 хв.)

- Домашнім завданням було:

- Для перевірки письмового завдання запрошую до дошки двох учнів.

- Для решти учнів я пропоную гру «Хрестики-ноликик». Ви поділяєтесь на 2 команди. Я зачитую запитання. Та команда, яка першою дає правильну відповідь, на ігровому полі ставить хрестик або нолик (відповідно до знаку своєї команди). Якщо на запитання команда відповідає неправильно, то у іншої команди є можливість дати правильну відповідь і поставити свій знак на ігровому полі. Увага! 

Запитання до гри:

1. Що таке многогранник?
2. Дайте означення призми?
3. Дайте означення піраміди?
4. Дайте означення паралелепіпеда?
5. Що таке бічне ребро многогранника?
6. Що таке бічна грань многогранника?
7. Що таке апофема?
8. Як знайти повну площу поверхні многогранника?

- І так, перемогла команда…. Кожен учень цієї команди отримує 4 бали. Протягом уроку ми будете мати можливість отримати додаткові бали і в кінці уроку отримати оцінку.

- Зверніть, будь ласка, увагу на дошку. Які є запитання щодо розв’язків задач домашнього завдання?

ІІІ Актуалізація вивченого матеріалу (9 хв.)

- А зараз я прошу вас подивись на слайд. Перед вами формули. Запитання наступне: для чого використовується дана формула? Учень, який знає правильну відповідь, піднімає руку і відповідає. За кожну правильну відповідь 1 бал.

- Ваші відповіді говорять про те, що теоретичний матеріал кожен з вас знає на достатньому рівні.

- У нас є учень, який виявив бажання приготувати презентацію по темі «Многогранники навколо нас». Давайте послухаємо.

- А зараз перевіримо, наскільки добре ви вмієте розв’язувати задачі, працюючи в невеликих групах. 

ІV Закріплення та осмислення вивченого матеріалу (11 хв.)

«Робота в малих групах»

- Прошу вас об’єднатися в групи по 4 чол. Таким чином з усіх учнів ми утворюємо «3 малі групи».

- Перед тим, як кожна група отримає завдання, пригадайте, як працювати в «малих групах» (див. пам’ятку) і розподіліть ролі. 

- Увага! Кожна група отримує модель многогранника.

Ваше завдання: зробити відповідні виміри і обчислити площу повної  поверхні многогранника.

- На виконання завдання відводиться 5 хвилин.

- Час вичерпаний. Запрошую до дошки доповідача з першої групи.

- Поясни, будь ласка, як ваша група розв’язувала задачу? Які формули ви використовували?

- Доповідь другої групи

- Доповідь третьої групи

Колективна робота (10 хв.)

Слово вчителя:

- Наступну задачу будемо розв’язувати письмово

Задача.  Основою піраміди є паралелограм, сторони якого 3см і 7см, а одна із діагоналей 6см. Висота піраміди проходить через точку перетину діагоналей і дорівнює 4см. Знайдіть бічне ребро піраміди.

Розв’язання.

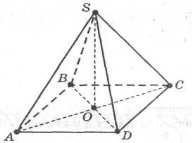
Оскільки SO(ABC), то SOAC, SOBD. За властивістю діагоналей паралелограма АО=ОС, ВО=ОD; ВО=½·ВD, ВО=3 см.

Оскільки SO (ABC), то SA, SB, SC, SD – похилі.

 SA=SC, SB=SD як похилі, які мають рівні проекції.

З прямокутного ∆ SOD (SOD=90⁰) за теоремою Піфагора маємо: , см, SB=SD=5см.

За властивістю паралелограма

cмv², АС=см, см.

З прямокутного ∆ SOА (SOА=90⁰) за теоремою Піфагора маємо:

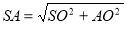
   см, SC=SA=6 cм.

Відповідь: 5 см, 6 см.

V Підбиття підсумків, оцінювання результатів уроку (3 хв.)

«Мікрофон»

- Чи була корисною сьогоднішня робота і чого ви навчилися

- Чи досягли ми очікуваних результатів?

- Які труднощі виникли у вас на уроці?

- А зараз будемо оцінювати роботу кожного учня на уроці (виставлення оцінок).

VІ Домашнє завдання та інструктаж до нього (2 хв.)