Урок з теми "Розв'язування задач на знаходження коородинат і векторів у просторі"

Тема уроку:   

Розв’язування задач на знаходження  координат та векторів у просторі

…нащадки будуть вдячні мені

не лише за те, що я сказав,

але і за те, що я не сказав

і тим самим дав їм можливість

і задоволення додуматися

до цього самостійно

Рене Декарт

Мета уроку:

• дидактична: повторити, систематизувати, узагальнити знання учнів про декартові координати та вектори в просторі;
• розвиваюча: розвивати в учнів логічне мислення; здійснювати самоконтроль
• виховна: виховувати любов до математики

Обладнання: мультимедійний проектор, картки із завданнями до конкурсів, дерев’яні діжки

Тип уроку: закріплення вивченого матеріалу

Методи і прийоми:  гра, «Мікрофон»

Очікувані результати:  після уроку учні зможуть:

• дати означення:

•            прямокутна система координат у просторі;
•            відстань між двома точками;
•            вектор;
•            рівність векторів;
•            дії над векторами
•            скалярний добуток векторів

• розв’язувати задачі на знаходження координат вектора за координатами його початку й кінця, довжини вектора, додавання та віднімання векторів, множення вектора на число, кут між векторами.

Хід уроку

І Організаційний момент (3 хв.)

Вступне слово.  

- Добрий день. Сідайте, будь ласка.

- Сьогодні у нас незвичайний урок, який пройде у вигляді гри.

- І для початку ми повинні поділитися на команди та вибрати журі (клас поділили на дві команди).

- Наше компетентне журі складається з __________________ ____________

- І так. Команди готові, журі – готове. Починаємо.

- Тема нашого уроку «Розв’язування задач на знаходження координат та векторів у просторі». Мета уроку: навчитися застосовувати набуті знання при розв’язуванні задач на знаходження координат та векторів у просторі.

Після уроку ви зможете:

• дати означення:

•            прямокутна система координат у просторі;
•            відстань між двома точками;
•            вектор;
•            рівність векторів;
•            дії над векторами
•            скалярний добуток векторів

• розв’язувати задачі на знаходження координат вектора за координатами його початку й кінця, довжини вектора, додавання та віднімання векторів, множення вектора на число, кут між векторами.

- Девізом нашого уроку є слова Рене Декарта «…нащадки будуть вдячні мені не лише за те, що я сказав, але і за те, що я не сказав і тим самим дав їм можливість і задоволення додуматися до цього самостійно» .

- Оголошуються Правила гри.

ІІ Проведення конкурсів (33 хв.)

Конкурс «Розминка»

Запитання задаються одній із команд. За кожну правильну відповідь – 1бал.

Запитання для першої команди

1. Які прямі називаються перпендикулярними в просторі?
2. Яка вісь називається віссю абсцис?
3. Чому дорівнює абсциса точки, яка лежить на вісі ординат?
4. Скільки існує точок із заданими координатами?
5. Які знаки мають координати точки, якщо вони належать другій чверті?

Запитання для другої команди

1. Які прямі називаються паралельними в просторі?
2. Яка вісь називається віссю ординат?
3. Чому дорівнює ордината точки, що лежить на вісі абсцис?
4. Скільки координат має задана точка?
5. Які знаки мають координати точки, якщо вони належать третій чверті?

Конкурс «Міні-тест»

Варіант 1 

1. Яка з точок А(7; 9; 0), В (0; -6; 8), С (-4; 0; 5) належить координатній площині хz?

а) точка А     б) точка В      в) точка С       г) жодна з наведених точок

2. Яка з наведених точок належить вісі Оz?

а) А (0; -7; 0)        б) В (8; 0; 0)         в) С (8; 0; 1)         г) К (0; 0; 6)

3. У якому із наведених випадків відрізок АВ перетинає площину ху?

а) А (0; 1; 2) і В (0; 1; 1)                б) А (-1; -1; 2) і В (5; -6; -7)

в) А (6; 7; 8) і В (-10; 10; 8)           г) А (2; 4; -11) і В (2; -4; -5)

Варіант 2

1. Яка з точок А(7; 9; 0), В (0; -6; 8), С (-4; 0; 5) належить координатній площині уz?

а) точка А     б) точка В      в) точка С       г) жодна з наведених точок

2. Яка з наведених точок належить вісі Ох?

а) А (1; 0; 1)        б) В (0; 0; 4)         в) С (-1; 0; 0)         г) К (1; 2; 0)

3. У якому із наведених випадків відрізок АВ перетинає площину хz?

а) А (0; 1; 2) і В (0; 1; 1)                б) А (-1; -1; 2) і В (5; -6; -7)

в) А (6; 7; 8) і В (-10; 10; 8)           г) А (2; 4; -11) і В (2; -4; -5)

Конкурс «Юний художник»

Для участі в цьому конкурсі потрібен 1 учень від команди.                   Завдання: намалювати картину.

(0;0),  (-1;1), (-3;1),  (-2; 3),  (-3;3),  (-4;6),  (0;8),  (2;5), (2;11), 

(6;10),  (3;9),  (4;5),  (3;0), (2;0), (1;-7), (3;-8),  (0;-8),  (0;0)

Конкурс «Танграм»

- Добра уява – це якість, необхідна в однаковій мірі й математику, й поету. Великий французький просвітитель Вольтер сказав, що Архімед мав більшу уяву, ніж Гомер.

Популярну китайську головоломку танграм називають розумовою головоломкою із семи частин. Назва танграм виникла в Європі, ймовірно від слів «тань», що означає «китаєць», і «грана», що означає «буква».

Завдання: Використовуючи всі сім частин скласти зображені фігури.

Конкурс капітанів

Капітанам дається однакові завдання, розв’язати яке потрібно протягом              3 хвилин.

1. Знайдіть координати вектора МК, якщо М (10; -4; 2) і К (16; 2; -5).
2. Знайти суму векторів 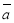 (1; -3; 2) і  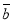(4; -5; -2).
3. Знайти косинус кута між векторами 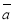(1; 2; 2) 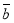(2; 3; 6).

Конкурс «Хто більше знає»

Команди по черзі витягують діжку із номером запитання. За правильну відповідь - 1бал.

1. Які вектори називаються рівними?

2. Як помножити вектор на число?

3. Як знайти суму двох векторів?

4. Як знайти різницю двох векторів?

5. Що таке скалярний добуток векторів?

6. Які вектори називаються колінеарними?

7. Які вектори називають компланарними?

8. Як знайти кут між векторами?

9. Які вектори називаються перпендикулярними?

10. Який вектор називається нульовим?

Конкурс «Розв’язати задачу»

1. Знайти косинус кута А трикутника АВС, якщо А (3; -1; 5) , В (-1; -1; 2),                   С (3; 1; 3).

2. При якому значенні m вектори (4; 2m; 5) і  (m; 3; 4) перпендикулярні?

V Підбиття підсумків, оцінювання результатів уроку (5 хв.)

«Мікрофон»

- Чи була корисною сьогоднішня робота і чого ви навчилися?

- Чи досягли ми очікуваних результатів?

- Чи сподобалась така форма проведення уроку?

VІ Домашнє завдання та інструктаж до нього  (2 хв.)