Урок з теми "Підготовка до ЗНО. Перпендикулярність прямих і площин."

Тема уроку: Повторення. Перпендикулярність прямих і площин у просторі

Мета уроку:

• узагальнити знання учнів з теми, вдосконалити  навички застосування теоретичного матеріалу до розв’язування практичних задач і підготовки до ЗНО;
• розвивати просторову уяву; логічне мислення учнів, навички порівняння,  вміння аналізувати, робити висновки;
• виховувати позитивне ставлення до навчання, наполегливість, прагнення до самовдосконалення, інтерес до геометрії та відповідальність.

Тип уроку: урок узагальнення і систематизації.

Перебіг  уроку:

1. Організаційний момент.
2. Мотивація до повторення та систематизації знань

Геометрія – це цілий світ, який оточує нас з самого народження, бо все, що ми бачимо навколо себе, так чи інакше, має відношення до геометрії.

Епіграф:  «Природа і життя людини формулює власні закони мовою математики.»                                             Г.Галілей

Урок  повторення,  узагальнення, систематизації  та  застосування знань, умінь, навичок  в рамках підготовки до ДПА та ЗНО.

Ми акцентуємо увагу на повтореннi за  такими питаннями:

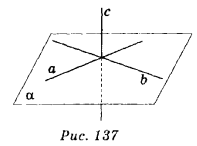
1. Означення перпендикулярних прямих і площин.
2. Ознаки перпендикулярності прямих і площин.
3. Властивості перпендикулярних площин.

ІІІ. Перевірка домашнього завдання. Самоперевірка. Графічний диктант

• «ні»                                   ˄    «так»

1. Якщо дві прямі лежать в одній площині то вони перетинаються
2. Через т. А, А? ά не належить прямій а, можна провести нескінчену множину прямих мимобіжних із прямою а.
3. Якщо дві прямі в просторі не перетинаються, то вони паралельні.
4. Якщо α||β, то для будь-якої прямої а площини α існує паралельна їй пряма в пл.: β.
5. Якщо кожна пряма площина α паралельна площині β, то α||β.
6. Якщо α||β, то будь-яка пряма площини α паралельна кожній прямій пл..β.
7. Якщо дві прямі, одна з яких лежить у пл..α, а друга – у пл..β, не мають спільних точок, то α||β.
8. Якщо а і в прямі, які не лежать в одній площині, то існує пряма с, що перетинає як пряму а, так і пряму в.
9. Через т. А, А є α можна провести єдину пряму, паралельну даній площині α.
10. Пряма,що лежить у площині має більш ніж одну спільну точку.
11. Якщо а||α,то пряма а паралельна будь-якій прямій площини α.
12. Через т. А, що не належить прямій а можна провести нескінчену множину площин, які проходять через т. А і паралельна прямій а.

4. Актуалізація опорних знань.

Систематизація та узагальнення теоретичного матеріалу.

1. Означення перпендикулярності прямої і площини

Уявлення про пряму перпендикулярну до площини дають вертика­льно поставлені стовпи — вони перпендикулярні до поверхні землі, пер­пендикулярні до будь-якої прямої, яка проходить через основу стовпа і лежить у площині землі.

Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину та перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину.

Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок прямої, перпендикулярної до площини, що міс­титься між даною точкою і площиною.

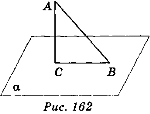На рис. 162 пряма AC перпендикулярна до площини α і перетинає її в точці С, отже, відрізок AC — перпендикуляр, опущений з точки А на площину α. Кінець цього відріз­ка, який лежить у площині, тобто точка С, називається основою перпендикуляра.

Якщо AC — перпендикуляр до площини α, а точка В — відмінна від С точка цієї пло­щини, то відрізок АВ називають похилою, про­веденою з точки А на площину α. Точка В — основа похилої. Відрізок, що з'єднує основи перпендикуляра і похилої, проведених з однієї і тієї самої точки, називається проекцією похилої.

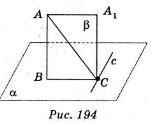
Теорема про три перпендикуляри

1. Якщо пряма проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до її похилої.
2. Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна до проекції цієї похилої.         

         

2. Ознака перпендикулярності прямої і площини.

Теорема.

Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.

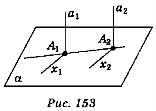3. Властивості прямої і площини, перпендикулярних між собою

Теорема 1.

Якщо площина перпендикулярна до од­нієї з двох паралельних прямих, то вона перпендикулярна і до другої.

Теорема 2.

Якщо дві прямі перпендикулярні до однієї і тієї самої пло­щини, то дані прямі паралельні.

 Теорема 3.

Якщо пряма перпендикулярна до однієї із двох паралель­них площин, то вона перпендикулярна і до другої.

Теорема 4.

Якщо дві площини, перпендикулярні до однієї і тієї самої прямої, то вони па­ралельні.

 

 

5. Вдосконалення навичок.

Усні вправи:

 

 

 

 

 

 

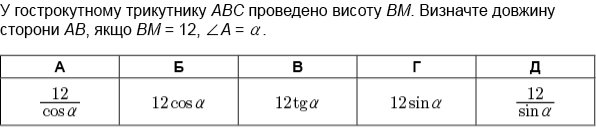
Д

 

 

 

 

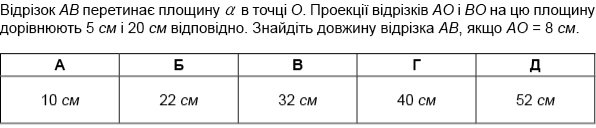
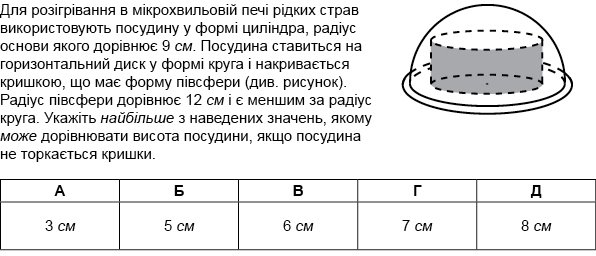
Г

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Г, Б, А, В

Письмове розв'язування задач формату ЗНО :

(45)

(5,25)

(96)

6. Хвилинка корисних порад
   1. Пам'ятайте – правильний малюнок шлях до правильного розв'язання задачі!
   2. Будь-який відрізок перпендикулярний стороні прямокутного трикутника утворює трикутник подібний даному.
   3. Запам'ятайте декілька Піфагорових трійок (сторони прямокутного трикутника):

3; 4; 5	6; 8; 10	9; 12; 15	12; 16; 20
5; 12; 13	10; 24; 26
8; 15; 17		24; 45; 51
7; 24; 25	14; 48; 50

 

• Альтернативні способи розв'язання

Відкинути завідомо неправильну відповідь.

Наприклад:

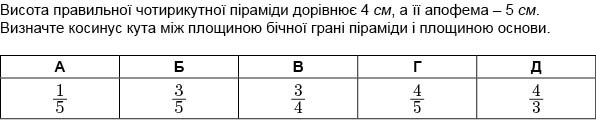
 1.Так як косинус кута не може бути більше 1, то відповідь Д неправильна.

2. Так як косинус – це відношення прилеглого катета до гіпотенузи, а апофема – це в даному випадку є гіпотенузою, то відповідь В неправильна.

3. Жодна сторона в трикутнику не дорівнює 1, то відповідь А неправильна

7. Підсумок  уроку. Тестове завдання – взаємоперевірка.

8. Домашнє завдання : повторити конспект, виконати завдання з тренувальних тестів..