Урок з теми "Розвязування неповних квадратних рівнянь"

Розв’язування неповних квадратних рівнянь

 урок математики

 у 8 класі

Мета:

удосконалювати уміння і навички розв’язувати неповні квадратні рівняння та рівняння, що зводяться до квадратних; розвивати  увагу, наполегливість, математичну мову, логічне мислення, виховувати культуру математичних записів.

Обладнання: картки із завданнями для індивідуальної роботи.

Девіз уроку: Швидкість потрібна, а поквапливість шкідлива.

Тип уроку: Урок формування умінь і навичок.

 Хід уроку.

1.Усна розминка.

- Яке рівняння називається квадратним?

- Яке  рівняння називається неповним квадратним?

- Як називаються числа а,в,с?

- Скільки розв’язків може мати неповне квадратне рівняння?

№ 1.Розв’язування завдань біля дошки.

1) 4х^2_  8х                                                2)х²                                                      3)х²

2.Перевірка домашнього завдання (фронтально).

3.Актуалізація опорних знань.

3.1.Інформаційне повідомлення.

Розв’язуванню квадратних рівнянь багато своїх праць присвятив відомий український математик, професор Микола Чайковський. (1887-1970). Він протягом тривалого часу працював у вищих навчальних закладах Кам’янця-Подільського, Львова, Одеси. М.Чайковський  зробив вагомий внесок у створення української наукової термінології з математики а також брав активну участь у виданні українських підручників з математики.

№ 2.Розв’язування дробово - раціональних рівнянь, що зводяться до неповних квадратних рівнянь

а).  ;         

    ^{Відповідь: Z}₁   ^Z₂         

б).=;

^{Відповідь:х}₁^=х₂⁼

^{3 Самостійна робота з наступною взаємоперевіркою.}

^{3.1.) Розв’язати рівняння.}

^а)х²⁺3х=0

^б).Х²=25

^в) х²-10х=0

^г) х²=100

4.Підсумок уроку. Домашнє завдання

Урок № 24

Тема. Властивості степеня (продовження). Степінь добутку й відношення

Мета: домогтися свідомого розуміння властивості степеня добутку й відношення; виробити вміння застосовувати ці властивості для перетво­рень виразів і обчислення значень числових виразів.

Тип уроку: засвоєння знань, умінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

Як і на попередніх двох уроках, перевірку домашнього завдання можна виконати у вигляді самостійної роботи (бліцконтроль), зав­дання якої є квінтесенцією завдань домашнього завдання.

Бліцтест

1. Яка з рівностей є правильною:

1) (y⁴)³ = y¹²; 2) (m⁵)⁴ = m²⁵; 3) ((a⁷)³)² = a²¹; 4) a³² : (a⁹)³ = a⁵?

2. Виконайте дії:
   1) m⁵m⁴; 2) (a⁶)³ · (a²)⁴; 3) (a⁵)³ · (a⁴)⁷ : a¹²; 4) (11³)⁴ : (11⁵)².
3. Подайте у вигляді степеня: .

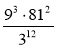Після виконання вправ звіряємо відповіді з відповідями у виконаному домашньому завданні.

III. Засвоєння знань

 Після проведеної роботи із випереджальним домашнім завданням все, що залишається для усвідомлення загальних властивостей, — це пройти ті ж самі етапи доведення, але для загальних випадків:

х²