Урок "Задачі про миттєву швидкість і дотичну до графіка функції"

Урок№_____

 Задачі про миттєву швидкість і дотичну до графіка функції

Мета уроку: Познайомити учнів із задачами, які приводять до по­няття похідної: задача про миттєву швидкість; зада­ча про дотичну до кривої.

І. Перевірка домашнього завдання.

II. Мотивація навчання.

Поняття похідної — фундаментальне поняття математичного аналізу, за допомогою якого досліджують процеси і явища в при­родничих, соціальних і економічних науках. Вивчення різних процесів (механічного руху, хімічних реакцій, розширення рідини при нагріванні, значення електричного струму та ін.) приводять до необхідності обчислення швидкості зміни різних величин, тобто до поняття похідної. Отже, наша найближча мета — по­знайомитися з поняттям похідної, навчитися знаходити похідні елементарних функцій та застосовувати поняття похідної до до­слідження функцій, вивчення деяких фізичних явищ, до ви­вчення геометричних понять.

III. Сприймання і усвідомлення поняття миттєвої швидкості прямолі-нійного руху матеріальної точки.

Якщо функція є математичною моделлю реального процесу, то часто виникає потреба знаходити різницю значень цієї функції у двох точках. Наприклад, позначимо через f(t) і f(t₀) суми коштів, які накопичилися на депозитному¹ рахунку вкладника до моментів часу t і t₀. Тоді різниця f(t) - f(t₀), де t > t₀, показує прибуток, який отримає вкладник за час t - t₀.

Розглянемо функцію у = f(х). Нехай х₀ — фіксована точка з області визначення функції f.

Якщо х — довільна точка області визначення функції f така, що х ≠ х₀, то різницю х - х₀ називають приростом аргументу функції f у точці х₀ і позначають ∆х (читають: «дельта ікс»)². Маємо:

∆х = х - х₀.

¹ Депозит (банківський вклад) — кошти, які вкладник передає банку на деякий строк, за що банк виплачує вкладнику проценти.

² Говорячи про приріст аргументу функції f у точці х₀, тут і далі припускатимемо, що в будь-якому інтервалі (х₀ - ε; х₀ + ε) є точки області визначення функції f, відмінні від х₀.

Звідси

х = х₀ + ∆х.

Говорять, що аргумент отримав приріст ∆х у точці х₀.

Зазначимо, що приріст аргументу може бути як додатним, так і від’ємним: якщо х > х₀, то ∆х > 0; якщо х < х₀, то ∆х < 0.

Якщо аргумент у точці х₀ отримав приріст ∆х, то значення функції f змінилося на величину

f(х₀ + ∆х) - f(х₀).

Цю різницю називають приростом функції f у точці х₀ і позначають ∆f (читають: «дельта еф»). Маємо:

∆f = f(х₀ + ∆х) - f(х₀)

або

∆f = f(х) - f(х₀).

Для приросту функції у = f(х) прийнято також позначення ∆у, тобто

∆у = f(х) - f(х₀) або ∆у = f(x₀ + ∆х) - f(х₀).

Приріст ∆х аргументу в точці х₀ і відповідний приріст f∆ функції показано на рисунку 35.1.

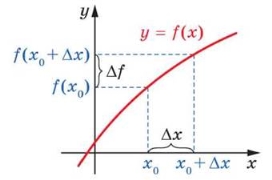
Рис. 35.1

Зауважимо, що для фіксованої точки х₀ приріст функції f у точці х₀ є функцією з аргументом ∆х.

ПРИКЛАД 1 Знайдіть приріст функції у = x² у точці х₀, який відповідає приросту ∆х аргументу.

Розв’язання. Маємо:

∆у = (х₀ + ∆х)² - х²⁰ = х²⁰ + 2х₀∆х + ∆х² - х² = 2х₀ ∆х + ∆х².

Відповідь: 2х₀∆х + ∆х².

Задача про миттєву швидкість

Нехай автомобіль, рухаючись прямолінійною ділянкою дороги в одному напрямку, за 2 год подолав шлях у 120 км. Тоді його середня швидкість руху дорівнює (км/год).

Знайдена величина дає неповне уявлення про характер руху автомобіля: на одних ділянках шляху автомобіль міг пересуватися швидше, на інших — повільніше, інколи міг зупинятися.

Разом із цим у будь-який момент часу спідометр автомобіля показував деяку величину — швидкість у даний момент часу. Значення швидкості в різні моменти повніше характеризує рух автомобіля.

Розглянемо задачу про пошук швидкості в даний момент часу на прикладі рівноприскореного руху.

Нехай матеріальна точка рухається по координатній прямій і через час t після початку руху має координату s(t). Тим самим задано функцію у = s(t), яка дає змогу визначити положення точки в будь-який момент часу. Тому цю функцію називають законом руху точки.

Наприклад, із курсу фізики відомо, що закон рівноприскореного руху задається формулою

де s₀ — координата точки на початку руху (при t = 0), v₀ — початкова швидкість, а — прискорення.

Нехай, наприклад, s₀ = 0, v₀ = 1 м/с, а = 2 м/с². Тоді s(t) = t² + t.

Зафіксуємо який-небудь момент часу t₀ і надамо аргументу в точці t₀ приріст ∆t, тобто розглянемо проміжок часу від t₀ до t₀ + ∆t. За цей проміжок часу матеріальна точка здійснить переміщення ∆s. Маємо:

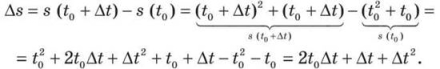
Середня швидкість vcep (∆t) руху точки за проміжок часу від t₀ до t₀ + ∆t дорівнює відношенню 

Отримуємо:

Позначення для середньої швидкості v_cep(∆t) наголошує, що при заданому законі руху у = s(t) і фіксованому моменті часу t₀ значення середньої швидкості залежить тільки від ∆t.

Якщо розглядати досить малі проміжки часу від t₀ до t₀ + ∆t, то з практичних міркувань зрозуміло, що середні швидкості v_cep (∆t) за такі проміжки часу мало відрізняються одна від одної, тобто величина v_cep(∆t) майже не змінюється. Чим менше ∆t, тим ближчим є значення середньої швидкості до деякого числа, що визначає швидкість у момент часу t₀. Іншими словами, якщо при ∆t  0

значення v_сер(∆t) прямують до числа v (t₀), то число v (t₀) називають миттєвою швидкістю в момент часу t₀.

Якщо в наведеному прикладі ∆t  0, то значення виразу 2t₀ + 1 + ∆t прямують до числа 2t₀ +1, яке є значенням миттєвої швидкості v (t₀), тобто

Цей приклад показує, що коли матеріальна точка рухається за законом у = s(t), то її миттєву швидкість у момент часу t₀ визначають за допомогою формули

тобто

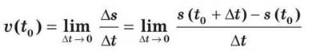
Задача про дотичну до графіка функції

Відоме означення дотичної до кола як прямої, що має з колом тільки одну спільну точку, незастосовне у випадку довільної кривої.

Наприклад, вісь ординат має з параболою у = х² тільки одну спільну точку (рис. 35.2). Проте інтуїція підказує, що неприродно вважати цю пряму дотичною до цієї параболи. Разом з тим у курсі алгебри ми нерідко казали, що парабола у = х² дотикається до осі абсцис у точці х₀ = 0.

Уточнимо наочне уявлення про дотичну до графіка функції.

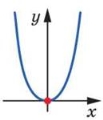
Рис. 35.2

Нехай М — деяка точка, що лежить на параболі у = х². Проведемо пряму ОМ, яку назвемо січною (рис. 35.3). Уявимо собі, що точка М, рухаючись по параболі, наближається до точки О. При цьому січна ОМ буде повертатися навколо точки О. Тоді кут між прямою ОМ та віссю абсцис ставатиме все меншим і меншим, а січна ОМ прагнутиме зайняти положення осі абсцис. Пряму, положення якої прагне зайняти січна ОМ з наближенням точки М до точки О, називатимемо дотичною до параболи у = х² у точці О.

Розглянемо графік деякої неперервної в точці х₀ функції f і точку М₀ (х₀; f(х₀)).

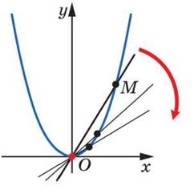
Рис. 35.3

У точці х₀надамо аргументу приріст ∆х і розглянемо на графіку точку М (х; f(х)), де х = х₀ + ∆х (рис. 35.4).

З рисунка видно, що коли ∆х стає все менше й менше, то точка М, рухаючись по графіку, наближається до точки М₀. Якщо при ∆х  0 січна М₀М прагне зайняти положення деякої прямої (на рисунку 35.4 це пряма М₀Т), то таку пряму називають дотичною до графіка функції f у точці М₀.

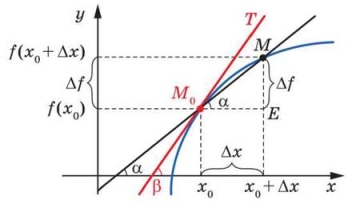
Рис. 35.4

Нехай січна М₀М має рівняння у = kx + b і утворює з додатним напрямом осі абсцис кут а. Як відомо, кутовий коефіцієнт k прямої М₀М дорівнює tg а, тобто k = tg а. Очевидно, що ∠MM₀E = а (рис. 35.4). Тоді з трикутника ММ₀Е отримуємо:

Уведемо позначення k_січ (∆х) для кутового коефіцієнта січної М₀М, тим самим підкреслюючи, що для даної функції f і фіксованої точки х₀ кутовий коефіцієнт січної М₀М залежить від приросту ∆х аргументу.

Маємо:

Нехай дотична М₀Т утворює з додатним напрямом осі абсцис кут β (β ≠ 90°). Тоді її кутовий коефіцієнт k (х₀) дорівнює tg β.

Природно вважати, що чим менше ∆х, то тим менше значення кутового коефіцієнта січної відрізняється від значення кутового коефіцієнта дотичної. Іншими словами, якщо ∆х  0, то k_cіч (∆x)  k (х₀).

Узагалі, кутовий коефіцієнт дотичної до графіка функції f у точці з абсцисою х₀ визначають за допомогою формули

тобто

Виконання вправ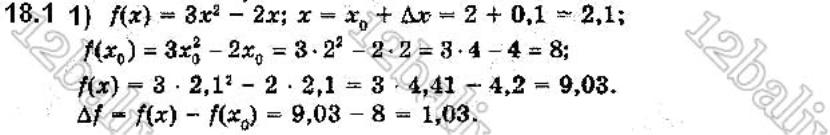

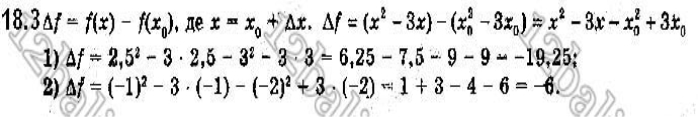
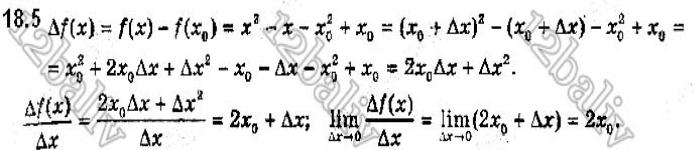
V. Підведення підсумків уроку.

VI. Домашнє завдання.

______________________________________________________________________