Урок захисту проектів "Теорема Піфагора-це головна і найкраща теорема геометрії"

                 Урок захисту проектів  з  геометрії  у  8 класі

«Теорема Піфагора – це головна і найкраща теорема геометрії»

Мета проекту:

 ознайомити учнів з біографією Піфагора та історією виникнення теореми, різними способами її доведення, розглянути застосування теореми при розв язуванні задач, показати практичне застосування теореми;

розвивати у учнів уміння і навички роботи з додатковою літературою, інтернет ресурсами, уміння шукати, обирати ,аналізувати знайдену інформацію та наглядно її подавати за допомогою комп ютера;

виховувати інтерес до предмета, уміння працювати у групах, показувати прикладне значення знань з математики.

Обладнання: персональний комп ютер, мультимедійний проектор, презентації.

Підготовка проекту

Обрати тему проекту. Проект - від лат. – кинутий уперед.        Вибір теми – це вибір проблеми, над якою будете працювати.
Визначити мету і завдання дослідження. Визначити мету дослідження – означає відповісти на запитання про те, навіщо ви будете працювати над цією проблемою.
Висунути гіпотезу дослідження. Це  прогнозування результатів дослідження.
Організувати дослідження. Аналіз та опрацювання інформаційних джерел:
Переглянути книги з теми.             Використати джерела Інтернету.	Записати важливу інформацію, яку дізналися з книг. Записати найцікавіше, що дізналися за допомогою Інтернету.
ІІ. Складання плану дослідження та аналіз результатів:
Провести спостереження.               Провести експеримент.    Провести анкетування.	Записати цікаву інформацію про результати спостережень. Записати план і результати експерименту. Проаналізувати та систематизувати результати анкетування.
Оформити результати проектної діяльності. Підготувати наочно-графічний або комп'ютерний продукт: Необхідно розкрити суть проекту та його структуру;  висвітлити  актуальність проекту у презентації;             здійснити аналіз інформації та форму­лювання висновків.
Організувати презентацію і захист проекту. Показати розуміння проблеми, мети, завдання; знайдений спосіб вирішення проблеми, висновки,                                                        прак­тичне спрямування проекту й значущість виконаної роботи.
Провести рефлексію.                                                                                  Рефлексія (від лат. – звертання назад) – процес самопізнання учнем внутрішніх психічних дій і станів, міркування, самоспостереження, самопізнання.

 

                                          Хід уроку

І. Організаційний момент.

Створення найрізноманітніших проектів є ознакою сьогодення. Майже місяць ви працювали над навчальним проектом «Теорема Піфагора – це головна і найкраща теорема геометрії»

Вивчали історичні відомості з даної теми і робили несподівані висновки.

 Перевіряли на практиці теоретичні знання, здійснювали дослідницьку діяльність.

Забезпечували зв'язок теорії з практикою, показуючи необхідність цих знань в житті.

Здійснювали пошукову та творчу діяльність, знаходячи вірші про теорему Піфагора та складаючи кросворди.

Вчилися самостійно працювати з джерелами інформації.

Вчилися аналізувати, систематизувати, узагальнювати отриманий матеріал, робити висновки.

Набували життєвого досвіду, вміння працювати в колективі, формувати власну життєву позицію.

Сьогодні групи біографів, науковців, практиків презентують результати своєї діяльності.

ІІ. Мотивація навчальної діяльності.

Під час того, як кожна з груп буде по черзі захищати підготовлені презентації, публікації, учні інших груп повинні слухати уважно, оскільки в кінці уроку потрібно буде не тільки оцінити захист товаришів з інших груп, але й відповісти на їх запитання за змістом презентації

ІІІ. Захист проектів

 Про Піфагора відомо лише те, що нічого неможливо стверджувати точно. Про нього написано одночасно і багато і мало. Ім я вченого обросло великою кількістю легенд. І на  сьогодні  група біографів зібрала нам інформацію про життя , діяльність Піфагора та його учнів-піфагорійців та подала цю інформацію у вигляді газети, яку ви зможете почитати пізніше, а зараз вони проанансують зміст деяких статей.

-Захист групи «Біографи»

1. Біографія Піфагора.

Він жив у VI столітті до нашої ери. Датою народження Піфагора вважається 570 рік до н. е., місцем — острів Самос. Про життя вченого достовірно відомо небагато. Біографічні дані в давньогрецьких джерелах переплітаються з явним вигадкою. На сторінках трактатів він постає великим мудрецем, чудово володіє словом і умінням переконувати. До речі, саме тому грецького математика і прозвали Піфагором, тобто «котрі переконують промовою». За іншою версією, народження майбутнього мудреця передбачила Піфія. Батько в її честь назвав хлопчика Піфагором.
Мудрець навчався у великих умів того часу. Серед викладачів молодого Піфагора значаться Гермодамант і Ферекид Сиросский. Перший прищепив йому любов до музики, другий навчив філософії. Обидві ці науки залишаться в центрі уваги вченого протягом всього його життя.

Навчання довжиною в 30 років

За однією з версій, будучи допитливим юнаком, Піфагор залишив батьківщину. Він вирушив шукати знань в Єгипет, де пробув, за різними джерелами, від 11 до 22 років, а потім потрапив у полон і був відправлений у Вавилон. Піфагор зміг отримати користь з свого становища. Протягом 12 років він вивчав математику, геометрію і магію в стародавній державі. На Самос Піфагор повернувся тільки в 56 років. Тут в той час правил тиран Полікрат. Піфагор не зміг прийняти таку політичну систему і незабаром відправився на південь Італії, де розміщувалась грецька колонія Кротон.
Сьогодні не можна точно стверджувати, чи був Піфагор в Єгипті і Вавилоні. Можливо, він залишив Самос пізніше і відразу відправився в Кротоні.

 

2. Школа Піфагора.

Історія теореми Піфагора пов'язана з розвитком створеної грецьким філософом школи. Це релігійно-етичне братство проповідувало дотримання особливого способу життя, вивчав арифметику, геометрію та астрономію, займалося дослідженням філософської і містичної боку чисел. Всі відкриття учнів грецького математика приписувалися йому. Проте історія виникнення теореми Піфагора зв'язується стародавніми біографами тільки з самим філософом. Передбачається, що він передав грекам знання, отримані у Вавилоні та Єгипті. Є також версія, що він дійсно відкрив теорему про співвідношення катетів і гіпотенузи, не знаючи про досягнення інших народів.

 

3.Чому «Теорема ста биків?»

 В деяких давньогрецьких джерелах описується радість Піфагора, коли йому вдалося довести теорему. В честь такої події він наказав принести жертву богам у вигляді сотні биків і влаштував бенкет. Німецький письменник-романіст А. Шаміссо написав такий вірш:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.

Учитель: Історія теореми Піфагора налічує кілька тисячоліть. Твердження , що квадрат гіпотенузи дорівнює сумі квадратів катетів, було відомо ще задовго до народження грецького математика. Проте теорема Піфагора, історія створення та докази її зв'язуються  саме з цим ученим. Згідно з деякими джерелами, причиною тому послужив перший доказ теореми, який був приведений Піфагором.

І сьогодні група науковців  приготувала нам презентацію різних способів доведення теореми та пропонує деякі з них.

-Захист групи «Науковці» (презентація «Різні способи доведення теореми Піфагора», доведення біля дошки)

Учитель: теорема Піфагора дуже часто застосовується при розв язуванні задач. Третя група практиків розглянула такі задачі і пропонує вам розв язати деякі з них.

-Захист групи «Практики» («Застосування теореми Піфагора при розв язуванні задач» )

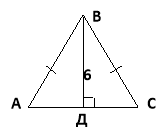1. Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6см. Знайдіть бічну сторону трикутника.

 

Дано:  АС – основа, АС = 16см,

ВД – висота, ВД = 6см.

Знайти: АВ.

Розв’язання:

 ∆АВС – рівнобедрений, ВД – висота.

За властивістю висоти рівнобедреного трикутника  ВД – медіана,

АД = ДС = 8см.

∆АВД – прямокутний, за теоремою Піфагора:  

Відповідь: 10 см.

 

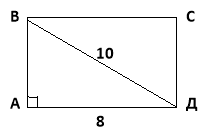
2. Діагональ прямокутника дорівнює 10см, а одна з його сторін 8см. Знайдіть периметр прямокутника.

                                                    Дано: АВСД – прямокутник, ВД – діагональ,             

                                                    ВД = 10см,  АД = 8 см.

Знайти: Р.

 

 Розв’язання:

 

                              Р = (АВ +ВС)× 2

 АВД – прямокутний трикутник, за теоремою Піфагора:

;  ;

Р = (6+8)× 2 = 28(см).

Відповідь: 28см.

 

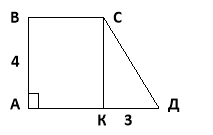
3. У прямокутній трапеції АВСД з основами АД і ВС, кут А – прямий,         АВ = 4дм. З вершини С до основи АД проведений перпендикуляр СК,          КД = 3дм,  Знайдіть СД.

     Дано: АВСД – трапеция, <А = , АВ = 4 дм.

СК АД , КД = 3 дм.

   Знайти: СД.

   Розв’язання:

                                                     Оскільки АВСД трапеція: АД//ВС, АВ//СК,

                                                     АВ = СК = 4дм.

                                                 Розглянемо ∆СДК, <К = 90°.

За теоремою Піфагора:  ;  ;

                                          .

Відповідь: 5дм.

Захист презентації «Застосування теореми Піфагора в повсякденному житті»

Самостійна робота з теми в тестовій формі

1) Если катеты равны 5 и 12, то гипотенуза равна:

А) 17;Б) 7;        В) 13;      Г) другой ответ;

2)Если гипотенуза равна 25 см, один из катетов 15 см, то второй равен:

А) 10 см;   Б) 35см;В) 20см;    Г)другой ответ

3)  Как называется сторона треугольника, лежащая против угла 90⁰?

А) катет; Б) основание    В) гипотенуза     Г) другой ответ;

4) Чему равна диагональ прямоугольника со сторонами 7см и 24см?

      А) 25см;   Б)31см;   В) 625см;   Г) другой ответ

           5) Чему равна сторона ромба, если диагонали равны 80см и 18см?

                    А) 98см;   Б) 80см;   В) 41см;     Г) другой ответ;

            6) Чему равен P египетского треугольника

                     А) 10; Б) 12; В) 20;Г) другой ответ;

              7) Чему равна диагональ квадрата со стороной 2 см?

                      A) 4 см; Б) √2  В) 8 см;Г) другой ответ

               8) Чему равен радиус окружности, описанной около треугольника с катетами 6 и 8 см;

                     А) 14см;  Б) 10см; В)5см; Г) другой ответ

               9)  Чему равна гипотенуза равнобедренного треугольника с катетом      а?

                      А) а√ 2; Б) 2а;   В) 4а; Г) другой ответ;

                 10)  Чему равны стороны египетского треугольника?

                        А)5,6,7Б) 3,4,5      В) 10,11,12Г) другой ответ;

                11) Чему равна площадь квадрата с диагональю  8 √2 см?

                      A) 32 см²; Б) 64 см; В) 128 см²; Г) другой ответ

                12) В прямоугольном  треугольнике с углом 30⁰, гипотенуза равна 10 см. Найти P                       треугольника

                    А) 30;    Б) 15+5 √3 см    В) 151  Г) другой ответ

Підсумки уроку

 Рефлексія учнів.  

1. Що нового дізналися, виконуючи проект?

2. Що було найскладнішим під час виконання проекту

3. Наскільки вагомою була ваша роль у групі?

4. Знання з яких предметів знадобилися вам під час виконання проекту?
5. Чи корисною була для вас робота?
6. Чи мали вплив інші люди на досягнення вами успіху на уроці?