Презентація "Доведення теореми Піфагора"
Про матеріал
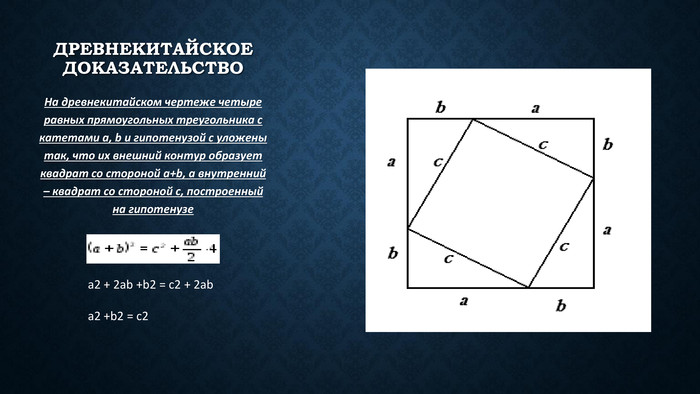
Презентація до уроку захисту проектів : різні способи доведення теореми Піфагора Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку