Урок "Застосування розв’язування прямокутних трикутників у прикладних задачах"
 Група експертів «Косинус»
Група експертів «Косинус»
 Група експертів «Синус»
Група експертів «Синус»
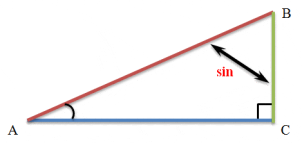
sin ![]() =
= ![]()


Геометричне доміно
Правила: Поділити картки доміно з запитаннями та відповідями. Починає той, у кого слово СТАРТ. Читається запитання, а інші учасники шукають відповідь на своїх картках. Зачитують її. Якщо відповідь вірна, то кладуть картку і читають наступне запитання уже зі цієї картки. І так до картки зі словом ФІНІШ.
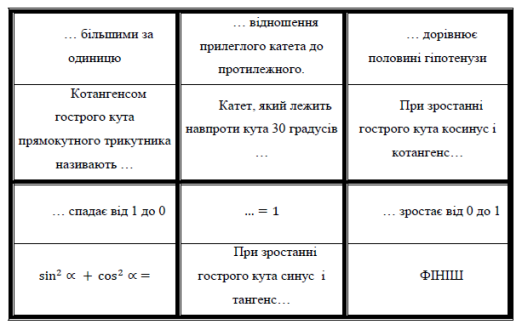
Тригонометричний пазл
Картинка розрізана на частини, на яких з іншого боку написані відповідні значення та завдання (зображені дзеркально), які мають відповідати завданням та значенням на картці з умовою. Встановіть відповідність і складіть пазл.
Чи відома Вам дана споруда?


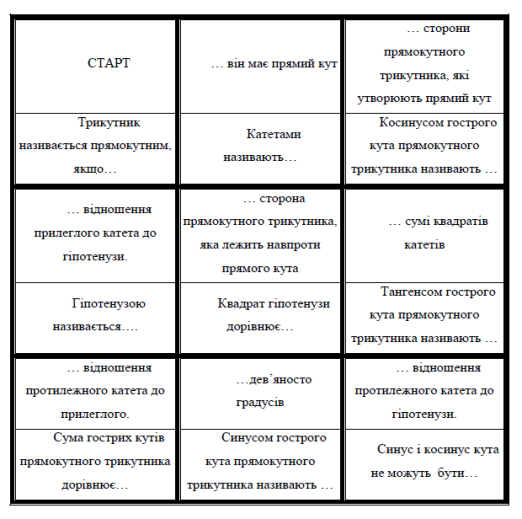
Геометричне доміно
Правила: Поділити картки доміно з запитаннями та відповідями. Починає той, у кого слово СТАРТ. Читається запитання, а інші учасники шукають відповідь на своїх картках. Зачитують її. Якщо відповідь вірна, то кладуть картку і читають наступне запитання уже зі цієї картки. І так до картки зі словом ФІНІШ.
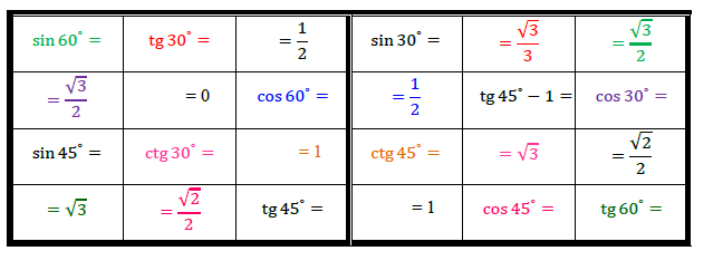
Тригонометричний пазл
Картинка розрізана на частини, на яких з іншого боку написані відповідні значення та завдання (зображені дзеркально), які мають відповідати завданням та значенням на картці з умовою. Встановіть відповідність і складіть пазл.
Чи відома Вам дана споруда?
Карта самооцінювання
…..……………………….
|
№ з/п |
Завдання |
Кількість балів |
Оцінка
|
|
1 |
Гра «Вірю – не вірю» |
1 |
|
|
2 |
Завдання І етапу «Теоретичний» (Plikers) |
4 (8 по 0,5) |
|
|
3 |
Завдання ІІ етапу «З геометрією по життю» |
2 |
|
|
4 |
Завдання ІІІ етапу «Геометричні ігри» |
1 |
|
|
5 |
Завдання ІV етапу «Будівництво веж» |
2 |
|
|
6 |
Завдання V етапу «Геометрія іде на допомогу» |
2 |
|
|
|
Всього балів |
12 |
|

Карта самооцінювання
…..……………………….
|
№ з/п |
Завдання |
Кількість балів |
Оцінка
|
|
1 |
Гра «Вірю – не вірю» |
1 |
|
|
2 |
Завдання І етапу «Теоретичний» (Plikers) |
4 (8 по 0,5) |
|
|
3 |
Завдання ІІ етапу «З геометрією по життю» |
2 |
|
|
4 |
Завдання ІІІ етапу «Геометричні ігри» |
1 |
|
|
5 |
Завдання ІV етапу «Будівництво веж» |
2 |
|
|
6 |
Завдання V етапу «Геометрія іде на допомогу» |
2 |
|
|
|
Всього балів |
12 |
|




Урок геометрії у 8 класі
Тема уроку: Застосування розв’язування прямокутних трикутників у прикладних задачах.
Мета:
Навчальна:
- закріпити знання про тригонометричні функції гострого кута прямокутного трикутника;
- знаходити невідомі елементи прямокутного трикутника по відомих двом його елементам;
- застосовувати теоретичні знання для вирішення практичних завдань;
- удосконалювати уміння застосовувати теорему Піфагора при рішенні прикладних завдань;
- показати учням на прикладах її практичне вживання теореми Піфагора у повсякденному житті.
Розвиваюча:
- розвивати комунікативну компетентність, інтелектуальні та творчі здібності, пізнавальну активність, кмітливість, пам’ять, увагу, логічне мислення, математичну мову, вміння оволодівати необхідною інформацією, орієнтуватися в нестандартних ситуаціях,
- розширювати світогляд учнів;
- підвищувати інформаційну культуру учнів, інтерес до вивчення предметів природничо-математичного циклу .
Виховна: виховувати активність, дисциплінованість, самокритичність, самостійність, колективізм, взаємоповагу, уміння вислухати інших, здорове суперництво, інтерес до математичних знань.
Методи навчання:
- словесні (бесіда, пояснення, опитування)
- наочні (презентація);
- практичні (задачі, вправи, тести, завдання практичного змісту).
Тип уроку: інтегрований урок узагальнення та систематизації знань, умінь, навичок учнів.
Форми організації уроку: індивідуальна, групова, фронтальна.
Обладнання і основні джерела інформації: креслярські інструменти, комп'ютер, проектор, екран, презентація до уроку, роздатковий матеріал.
Структура уроку:
І. Організаційний момент.
ІІ. Перевірка домашнього завдання
ІІІ. Мотивація навчальної діяльності.
ІV. Повідомлення теми, мети і завдань уроку. Активізація опорних знань.
V. Узагальнення та систематизація знань, умінь, навичок.
VІ. Підбиття підсумків уроку.
VІІ. Домашнє завдання.
VІІІ. Рефлексія
Хід уроку
Світ, що нас оточує, - це світ геометрії.
Тож давайте його пізнавати!
Піфагор
- Організаційний момент
Вступне слово вчителя
Вітаю всіх присутніх у цьому класі!
Урок геометрії у нас на часі.
Тема заняття у нас така,
бо прямокутний трикутник – штука не проста!
До вивчення його основних властивостей запрошую я.
Слово вчителя
Відомий давньогрецький філософ, вчений та математик Піфагор якось зауважив: «Світ, що нас оточує, - це світ геометрії. Тож давайте його пізнавати!». На уроці ми втілимо бажання відомого вченого в життя і цей вислів стане епіграфом нашого уроку.
Можливо, знаходження невідомих елементів у прямокутному трикутнику комусь видається нудною справою. Переконаємо їх у протилежному.
У цьому сьогодні нам допоможуть дві математичні групи експертів. Це група «синусів» і «косинусів».
На столах кожної групи лежать індивідуальні картки самооцінювання. Підпишіть їх. У ході уроку ми з вами будемо виконувати різні завдання, за які ви отримаєте бали. Не забуваємо фіксувати свої результати.
ІІ. Перевірка домашнього завдання
- Перевірка виконання письмових задач у зошитах учнів.
- Перевірка теоретичного матеріалу.
Слово вчителя
А зараз ми перевіримо як ви знаєте теоретичний матеріал.
Проведемо з вами гру «Вірю – не вірю». За кожну правильну відповідь ви отримуєте по 1 балу, не забуваємо помічати це у картці самооцінювання.
Так чи ні:
1) У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. (так)
2) Сума гострих кутів прямокутного трикутника дорівнює 180 градусів (ні).
3) Основна тригонометрична тотожність має вигляд: sin2α + cos2α = 1 (так)
4) Трикутник у якого є прямий кут називається гострокутним (ні)
5) Сторона прямокутного трикутника, що лежить проти прямого кута називається гіпотенуза (так)
6) Гіпотенуза більша за будь-який катет (так)
7) Відношення протилежного катета до гіпотенузи в прямокутному трикутнику називається тангенсом кута (ні)
8) Розв'язати прямокутний трикутник означає знайти його всі сторони і кути за відомими сторонами і кутами (так)
Фіксуємо свої результати (1 бал за кожну правильну відповідь + якщо були доповлення)
ІІІ. Мотивація навчальної діяльності
Слово вчителя
- Діти! Міцність будинку залежить від міцності фундаменту. Сила майбутніх знань часто залежить від сили попередніх. Тож давайте «побудуємо фундамент» для нових знань.
- Я бажаю кожному з вас до кінця уроку піднятися до останньої сходинки «Успіх».
«Трикутник є першою фігурою, яка не може розкластися в інший вигляд більш простої фігури…і тому є першим фундаментом будь-якої речі, яка має границю і форму». (Джордано Бруно, італійський учений)
Бесіда
Отже, розмова на уроці буде йти про що? Так, про трикутники.
Що в хімії вивчають спочатку? Так, елементи, а потім – їх сполуки.
А в біології? Так, одноклітинні, а потім – багатоклітинні організми, так і в геометрії – точки, відрізки і точки, відрізки і трикутники, з яких складаються інші геометричні фігури.
Серед цих фігур прямокутний трикутник грає особливу роль. Чому?
Бо, будь-який многокутник можна розбити на трикутники, уміючи знаходити кутові і лінійні елементи цих трикутників, можна знайти всі елементи багатокутника. У свою чергу, будь-який трикутник можна розбити одній з його висот на два прямокутні трикутники, елементи яких зв'язані простішою залежністю.
Слово вчителя
Записуємо тему уроку у зошит «Застосування розв’язування прямокутних трикутників у прикладних задачах»
На уроці ми закріпимо знання про тригонометричні функції гострого кута прямокутного трикутника і застосуємо їх для вирішення прикладних задач.
У кожної групи на парті роздатковий матеріал по темі уроку.
Сьогодні ми з вами проведемо математичну естафету, яка складається із 5 етапів.
Перший етап «Теоретичний»
Слово вчителя. Пропоную всім учасникам кожної групи виконати тестові завдання. І зробимо це за допомогою інтерактивного ресурсу Plikers (у кожного учня індивідуальна картка з QR-кодом, яку необхідно розмістити, щоб буква, яка є відповіддю, на думку учня, знаходилась зверху). За кожну правильну відповідь отримуєте 0,5 бала (максимум 4 бали за тестові завдання).
1. Що називають синусом гострого кута прямокутного трикутника?
а) відношення прилеглого катета до гіпотенузи;
б) відношення протилежного катета до гіпотенузи;
в) відношення протилежного катета до прилеглого;
г) відношення прилеглого катета до протилежного.
- Що називають косинусом гострого кута прямокутного трикутника?
а) відношення прилеглого катета до гіпотенузи;
б) відношення протилежного катета до гіпотенузи;
в) відношення протилежного катета до прилеглого;
г) відношення прилеглого катета до протилежного.
- Що називають тангенсом гострого кута прямокутного трикутника?
а) відношення прилеглого катета до гіпотенузи;
б) відношення протилежного катета до гіпотенузи;
в) відношення протилежного катета до прилеглого;
г) відношення прилеглого катета до протилежного.
- Що називають котангенсом гострого кута прямокутного трикутника?
а) відношення прилеглого катета до гіпотенузи;
б) відношення протилежного катета до гіпотенузи;
в) відношення протилежного катета до прилеглого;
г) відношення прилеглого катета до протилежного.
- Якщо катети прямокутного трикутника дорівнюють 6 см і 8 см, то його гіпотенуза дорівнює…
а) 5 см; б) 2√7 см; в) 4√7 см; г) 10 см;
- Знайдіть синус кута А
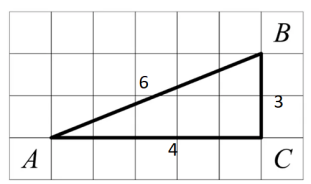
а) 1/2;
б) 4/6;
в) 4/3;
г) 3/4.
- Знайти sin 45°.
а) √3/2; б) √2/2; в) 1/√3; г) ½;
- Знайти tg 45°.
а) √3; б) √2/2; в) 1/√3; г) 1;
Переходимо до другого етапу
Другий етап «З геометрією по життю»
Слово вчителя
Прямокутний трикутник має широке вживання в повсякденному житті – багато геометричних і практичних завдань зводяться до обчислення елементів прямокутного трикутника, іншими словами до розв’язування прямокутного трикутника.
По одному учню від команди розв’язують задачі на дошці.
Завдання для команди «Синус»
Слово вчителя
А що ви знаєте про професію пілота?
Відповіді учнів
Льотчик керує літаком. Політ складається з декількох етапів: зліт, набір висоти, горизонтальний рух, зниження і посадка. Зліт і посадка – найвідповідальніші моменти польоту. Адже поблизу аеропорту може знаходитись декілька бортів. Найменше відхилення від розрахункової треєкторії погрожує зіткненням. При зльоті і посадці пілот не тільки відслідковує інформацію, але і думкою аналізує її, зіставляючи дані приладів з тим, що він бачить з вікна кабіни: враховує погодні умови і особливості керування конкретним повітряним судном.
Задача (картка). Пасажирський літак, який перебуває над пунктом А на висоті 400 м, почав посадку на злітну смугу аеродрому. Знайдіть кут приземлення літака, якщо аеродром знаходиться на відстані 1,2 км від пункту А.
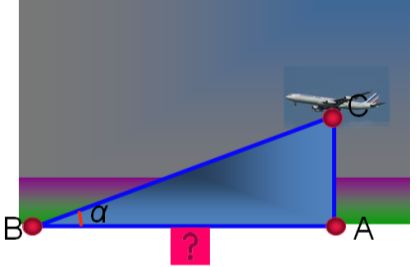
Розв’язання:
АС = 400 м
АВ = 1,2 км = 1200 м
tg α = АC : AB = 400 : 1200 =
= 1/3 = 0,3333,
α = 180
У ролі грамотного пілота у нас побував …………………………
Завдання для команди «Косинус»
 Дах будинку є несучою конструкцією, яка бере на себе все зовнішнє навантаження. Основою даху будь-якого будинку є кроквяна система. У більшості будинків нашого населеного пункту двосхилий дах, де простір горища грає роль теплозахисту.
Дах будинку є несучою конструкцією, яка бере на себе все зовнішнє навантаження. Основою даху будь-якого будинку є кроквяна система. У більшості будинків нашого населеного пункту двосхилий дах, де простір горища грає роль теплозахисту.
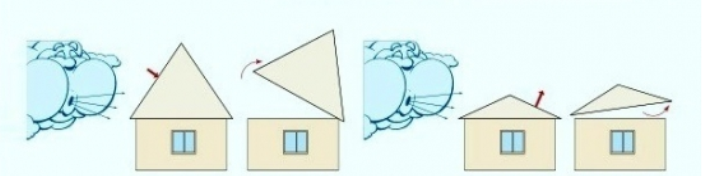 Під час будівництва такого даху необхідно чітко прораховувати довжину крокв та їх кут нахилу до стелі. Оптимальний кут нахилу двосхилого даху лежить в межах від 20° до 45°, що відповідає усередненим кліматичним параметрам.
Під час будівництва такого даху необхідно чітко прораховувати довжину крокв та їх кут нахилу до стелі. Оптимальний кут нахилу двосхилого даху лежить в межах від 20° до 45°, що відповідає усередненим кліматичним параметрам.
Пропоную вам уявити себе у ролі будівельника і розв’язати задачу.
Задача (картка). Ширина будинку 7 м довжина крокви 5 м. Під яким кутом
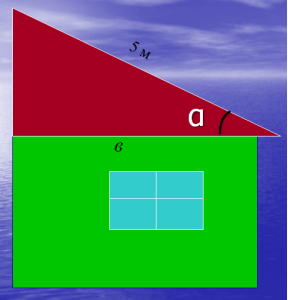 крокви нахилені до стелі ?
крокви нахилені до стелі ?
Розв’язання:
с = 5 м, в = 3,5 м. - ?
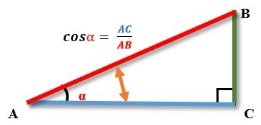
cos = ![]()
cos = ![]() = 0.7, = 450
= 0.7, = 450
У ролі досвідченого будівельника у нас побував ……………………………………
Третій етап «Геометричні ігри»
Слово вчителя
Пропоную обом групам зіграти у геометричну гру.
Четвертий етап «Будівництво веж»
Слово вчителя
- Діти, яка країна Європи має форму «чобітка»? (Італія)
- Які визначні місця чи пам’ятки архітектури Італії вам відомі? (античні Помпеї, будинок Джульєти, Пізанська вежа, місто Венеція, римський Колізей, …)
 Подорожуючи по Італії обов'язково відвідайте Пізу. Місто Піза розташоване в Центральній Італії, його історія налічує не одну тисячу років, але прославилося воно на весь світ, завдяки помилці архітектора. Звичайно ж, не важко здогадатися, що мова йде про падаючу Пізанську вежу, мабуть, найвідомішу пам'ятку Італії.
Подорожуючи по Італії обов'язково відвідайте Пізу. Місто Піза розташоване в Центральній Італії, його історія налічує не одну тисячу років, але прославилося воно на весь світ, завдяки помилці архітектора. Звичайно ж, не важко здогадатися, що мова йде про падаючу Пізанську вежу, мабуть, найвідомішу пам'ятку Італії.
Пізанська вежа — частина міського собору Санта Марія в Пізі. Вежа є дзвіницею собору і відома тим, що сильно нахилена.
Висота вежі становить 56 метрів, діаметр — 15 метрів, діаметр фундаменту 19,6 метра. На вершину вежі ведуть сходи з 294 сходинок, піднявшись якими на саму гору, можна оглянути всю околицю. Будівництво дзвіниці кафедрального собору розпочалось 9 серпня 1173 року, архітектором Бонанно Пізано і тривало з двома перервами майже 200 років. Ледве будівництво досягло третього ярусу, як вежа почала просідати в землю через поганий фундамент, і нахил став очевидним.
 В даний час ведуться роботи з укріплення Пізанської вежі з метою зберегти її для нащадків.
В даний час ведуться роботи з укріплення Пізанської вежі з метою зберегти її для нащадків.
Завдання для команди «Косинус»
Задача (картки). Визначити кут нахилу вежі, якщо нам відома її висота – 56 м і те, що вершина вежі була відхилена на відстань приблизно 5 м від центру.
Розв’язання: АС = 5 м, ВС = 56 м,
tg В = 5/56 = 0,0893, кут В = 50
Відповідь: 50.
Слово вчителя
Команда «Косинусів» вирахувала кут нахилу Пізанської вежі. Майбутній менеджер туристичної компанії …………………………… швидко справилася з цим завданням.
Завдання для команди «Синус»

Радіовежа (радіощогла, радіобашта, телевежа, телебашта, телевізійна вежа) — висока структура, призначена задля підтримки антен для телекомунікації та трансляції
(передавання) радіосигналу, у тому числі
телебачення. Ці структури є одними з найбільш
високих, збудованих людиною.
Для стійкості конструкції її закріплюють тросами.
Задача (картки). Висока радіовежа закріплена тросами. Яку довжину має трос, якщо точка А знаходиться на відстані 75 м від основи вежі, і трос закріплено під кутом 590 до землі?
Розв’язання: sin 590 = ![]() , c =
, c = ![]() = 87,5 м.
= 87,5 м.
Слово вчителя
Пора нам зробити перерву і трішки відпочити для відпочинку. Давайте ми з вами порелаксуємо.
Релаксація
Встали всі рівненько.
1. Покажіть головний кут прямокутного трикутника.
2. Два прямих кута.
3. Доповніть двома гострими кутами: один і один.
Фізкультхвилинка «Добре»
Добре те, що сонце світить (підняти руки вгору)
Добре те, що віє вітер (коливання рук)
Добре те, що весна надворі (потерти долоні)
Добре вчитися у школі (підстрибнути, ноги всторону і здійснити хлопки руками над головою)
Добре друзів вірних мати (розвести руки в сторони)
Математику вивчати (здійснити із взмахом руки уклін до землі)
П’ятий етап «Геометрія іде на допомогу»
Задача для команди «Синус»
Задача «Морська навігація». Корабель у морі видно під кутом 90. Відстань від кімнати обзору маяка до корабля 1150 м. Яка відстань від маяка до корабля?

Задача для команди «Косинус»
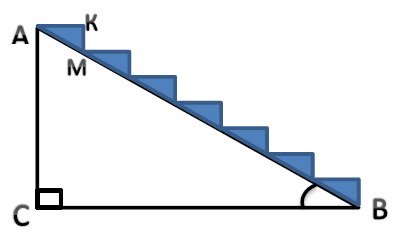
 Задача «Ескалатор». Ескалатор метрополітену містить 170 східців від вестибюля до підлоги підземної станції. Ширина сходинки ескалатора – 40 см, висота – 20 см. Обчисліть глибину станції та кут нахилу ескалатора.
Задача «Ескалатор». Ескалатор метрополітену містить 170 східців від вестибюля до підлоги підземної станції. Ширина сходинки ескалатора – 40 см, висота – 20 см. Обчисліть глибину станції та кут нахилу ескалатора.
- Шановні мої експерти-професіонали! Ви вміло справилися з усіма задачами, маю надію, що колись вам знадобляться набуті знання щодо розв’язування прямокутних трикутників.
- Ми з вами побачили важливість і практичність даної теми. Тому хочу, щоб ви товаришували з прямокутним трикутником!
Рефлексія
Учитель пропонує кожному учневі оцінити свою роботу, але спочатку пропонує послухати притчу.
Ішов мудрець. Йому назустріч ішло троє людей, які під палючим сонцем везли візок із каменями для будівництва. Мудрець зупинив їх і поставив кожному одне й те ж запитання: «Що ти робив цілий день?»
Перший відповів: Я цілий день возив прокляті камені.
- А я сумлінно виконував свою роботу – сказав другий.
- Я брав участь у будівництві храму. – посміхнувся третій, і його обличчя засяяло посмішкою.
- А як ви оціните свою роботу на уроці? Хто працював як перший - піднімає жовту картку, хто як друґий - зелену, а хто як третій - червону.
Учитель робить висновок Бажаю всім працювати з радістю і задоволенням.
Підсумок уроку
Дякую!!! Ви добре подолали всі п’ять етапів математичної естафети! Тож підведемо підсумки.
Метод «Чотири Що?»
- Що ви дізналися, навчилися на уроці?
- Що сподобалося найбільше?
- Що було найскладнішим?
- Що треба ще вивчити?
Закінчіть, будь ласка, речення:
- Було цікаво.. розв’язувати деякі задачі
- Було складно... працювати на уроці
- Я виконував завдання... задоволенням чи були труднощі
- Я зрозумів ... зможу виконати домашнє завдання
- Я запам’ятав…
Вербальне оцінювання
- Ти на правильному шляху!
- Ти можеш краще!
- Досить вдало! Я радію за тебе!
- Бездоганна робота!
- Значно краще! Так тримати!
- У тебе все вийде, доопрацюй!
- Відмінно! Прекрасно! Бездоганно!
- Вітаю! Це те, що треба!
Домашнє завдання
Підготувати прикладну задачу, де застосовується розв’язування прямокутних трикутників.
Урок закінчено. Дякую за співпрацю!
1


про публікацію авторської розробки
Додати розробку
