Урок "Застосування визначеного інтеграла (професія "перукар")"

Тема: Застосування визначеного інтеграла.

   (ПРОФЕСІЯ ПЕРУКАР)

Мета уроку: 

Тип уроку:  урок узагальнення та систематизації навчального матеріалу.

Обладнання: навчальний клас, дошка, крейда, екран, проектор, комп’ютер, презентація в редакторі PowerPoint, plickers.com

Очікувані результати:  учням необхідно

знати:  таблицю первісних елементарних функцій,   правила знаходження первісних, формулу Ньютона – Лейбниця, таблицю інтегралів;

вміти: знаходити первісну з використанням таблиці  первісних та  правил знаходження первісних, застосовувати формулу Ньютона – Лейбниця до обчислення  визначеного інтеграла, обчислювати за допомогою інтеграла площу криволінійної  трапеції, застосовувати інтеграл до розв’язування задач стереометрії, фізики, економіки, техніки.

ДЕВІЗ УРОКУ: «Світ, що нас оточує – це світ інтегрального і диференціального числення. Тож давайте його пізнавати»  Х. Гюйгенс

ХІД УРОКУ

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ     

ІІ. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ  

       Ми з вами сьогодні спробуємо за допомогою математики розв’язати  проблеми, що виникають на уроках фізики, економіки та інших сфер діяльності людини. До речі, задача (англ. problem) означає "проблема". Проблема розв’язування задач ускладнюється в тому випадку, якщо вміння побачити єдину математичну модель у різних ситуаціях недостатньо розвинене. Можливість розвивати ці уміння ви й матимете сьогодні, розв’язуючи задачі, пов’язані з геометрією, фізичними явищами, економічними процесами. І ви матимете чудову  нагоду закріпити і розвинути навички знаходити визначений інтеграл, застосовувати його при розв’язуванні практичних задач.

      Отже, відкрили зошити, записали дату і тему уроку «Застосування визначеного інтеграла»

ІІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ 

Фронтальне опитування із завданнями

V. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Групове тестування учнів за допомогою сервіса plickers.com. Наприкінці на екран виводиться таблиця з результатами і вчитель підводить підсумки.

VІ. УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ ВМІНЬ ТА НАВИЧОК

Девізом нашого уроку будуть слова голландського вченого Х. Гюйгенса

«Світ, що нас оточує – це світ інтегрального і диференціального числення.

Тож давайте його пізнавати».

Поняття інтеграла – важливе  як у шкільному курсі математики, так і в курсі вищої математики, що розгалужується на низку цікавих, хоч і складних, математичних дисциплін. Назву вам лише кілька з них:

• математичний аналіз,
• функціональний аналіз,
• теорія функції комплексної змінної,
• диференціальні рівняння,
• теорія ймовірностей,
• теорія оптимізації математичних процесів.

Окрім математичних, є науки, що широко використовують математичний апарат і нині дуже популярні, оскільки необхідні для ведення різноманітних справ, для гармонійного розвитку галузей виробництва, тощо. У цих науках також використовується поняття інтеграла. Серед них такі як:

• економіка виробництва,
• фінансова справа,
• електроніка,
• програмування,
• фізика,
• хімія,
• радіофізика, тощо.

А як можна поєднати дві непоєднувані речі: інтеграл та перукаря?

Давайте послухаємо….

Учень 1 (на фоні презентації)

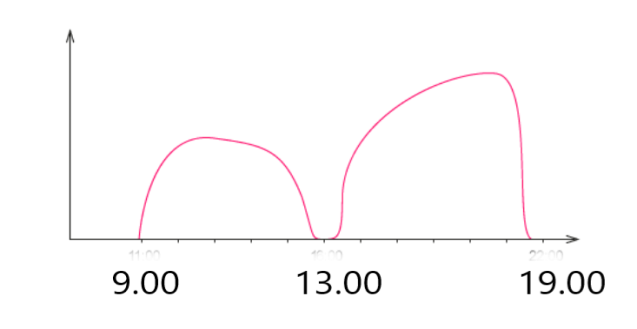Я-перукар. Що таке інтеграл і навіщо мені його знати? За приклад візьмемо швидкість моєї роботи на протязі дня

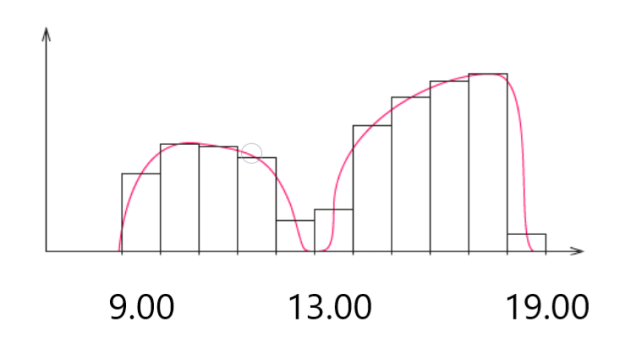Якщо в нас є такий графік, то можна порахувати, скільки роботи я зробила за день – це площа під графіком. Але як це порахувати? Поділимо графік на стовпці рівної ширини величиною в годину. А висоту цих стовпців зробимо рівною швидкості роботи в середині цього часу.

Площу кожного стовпця окремо легко порахувати: треба помножити його ширину на висоту. Виходить, що площа кожного стовпця – це скільки я роботи приблизно зробила за годину. А якщо просумуємо всі стовпці, то отримаємо мою роботу за день. Проблема у тому, що результат вийде приблизний, а нам потрібне точне число. Розіб’ємо графік на стовпці по пів години:

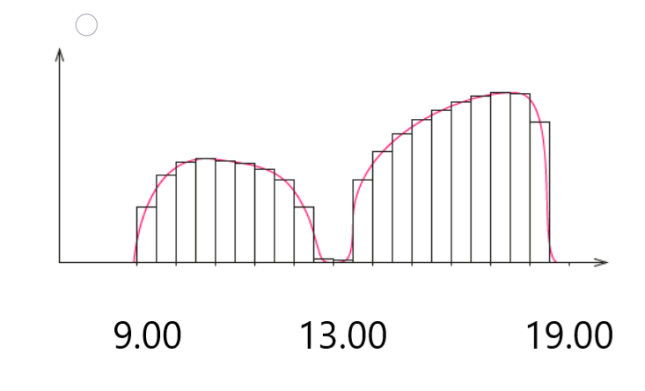
На картинці видно, що це вже набагато більше до того, що ми шукаємо.

Так зменшувати відрізки на графіку можна до нескінченності, і кожного разу ми все ближче і ближче будемо наближатися до площі під графіком. Це називається інтегралом і позначається ось так

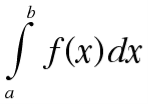
В цій формулі f(x) означає функцію, що залежить від величини х, а літери a,b – це відрізок, на якому ми хочемо знайти інтеграл.

Навіщо це потрібно? Вчені намагаються всі фізичні явища виражати через математичні формули. Як тільки в нас є формула, далі можна при її допомозі порахувати що завгодно. А інтеграл – це один з основних інструментів роботи з функціями. За допомогою інтегрування знаходят енергію, роботу, тиск, масу, електричний заряд і багато інших величин.

Вчитель

Давайте з’ясуємо, як саме ми можемо застосувати визначений інтеграл в таких науках, як геометрія, фізика, економіка.

Перша задача  буде пов’язана з фінансами

Учень 2 (розв’язує біля дошки задачу з поясненням, учні конспектують)

На полі пшениці після приземлення космічного корабля  залишився слід,  який нагадує  фігуру,  обмежену лініями  у = х² – 2х та  у = 3. Необхідно визначити збитки, завдані агрокомплексом, якщо з 1 м² отримують в середньому 3 кг пшениці, яка коштує 1 грн./кг.

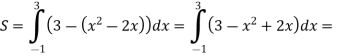
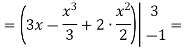
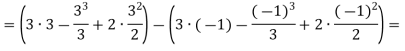
Учитель

Зараз послухаємо про історію народження інтегрального числення

Учень 3. (на фоні презентації) Моє повідомлення пов’язане «З історією інтегрального числення»

З історії інтегрального числення

Багато значних досягнень математиків Стародавньої Греції у розв’язуванні задач на знаходження квадратур (тобто обчислення площ) плоских фігур, а також кубатур (обчислення об’ємів ) тіл пов’язані із застосуванням  методу вичерпування, що запропонував Евдокс Кнідський (бл. 408-355рр. до н.е.). За допомогою цього методу Евдокс довів, що площі двох кругів відносяться, як квадрати їх діаметрів, а об’єм конуса дорівнює третині об’єму циліндра, з такою ж основою і висотою.

Цей метод удосконалив Архімед. Виведення формули площі круга в геометрії ґрунтується на ідеях Архімеда. За допомогою методу вичерпування і цілого ряду інших дотепних міркувань вчений розв’язав багато задач : дав оцінку числа π , знайшов об’єми кулі і еліпсоїда, площу сегмента параболи. Сам Архімед високо цінив ці результати: за його бажанням на могилі висікли кулю, вписану в циліндр.

Архімед передбачив багато ідей інтегрального числення. Але пройшло більш як півтори тисячі років, перш ніж ці ідеї знайшли чітке вираження і були доведені до рівня числення. 

Учитель

Певну суму знань про закономірності розвитку природи, взаємодію суспільства і природного середовища, про проблеми й завдання його охорони та збереження ми дістаємо, розв’язуючи задачі біологічного та екологічного змістів. Давайте розв’яжемо таку задачу

Учень 4 (розв’язує біля дошки задачу з поясненням, учні конспектують)

Знайти площу пелюстка ромашки, який розміщено  між дугами парабол

Розв’язання

Дана фігура обмежена графіками двох функцій: 

Шукана площа за допомогою інтеграла обчислюється так:

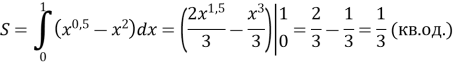
Відповідь. кв. од.

Учитель давайте послухаємо наступну доповідь про застосування інтегралів та вчених, що іх вивчали

Учень 5 (на фоні презентації)Я маю намір розповісти про «Застосування визначених інтегралів»

За допомогою визначених інтегралів обчислюють площі криволінійних фігур на площині, статистичні моменти, моменти інерції, роботу сили, потенціали. Наприклад, обчислюючи роботу сили, доводиться мати справу з функціями, аргументом яких є довжина кривої, відлічувана від певної точки на кривій, - криволінійна координата. Виникнення інтегрального числення пов’язане з потребою обчислення площ і об’ємів. Уже  в античній математиці для обчислення площ і об’ємів застосовували способи , схожі на обчислення  визначених інтегралів. Значних успіхів у цьому досяг давньогрецький математик  Архімед (ІІІ ст.. до н.е. ), який для розв’язування задач на обчислення площ і об’ємів застосовував метод вичерпування. (презентація)

Створенню інтегрального числення сприяли праці Й.Кеплера, Б.Кавальєрі, Е.Торрічеллі, Дж.Валліса , Б. Паскаля. Математики ХVІІ ст. не користувалися поняттям границі. Замість цього вони говорили про «суму нескінченно великої кількості нескінченно малих доданків». Учитель І.Ньютона І.Барроу встановив зв'язок між диференціюванням та інтегруванням у геометричній формі, а І.Ньютон і Г.Лейбніц незалежно один від одного в кінці ХVІІ ст. розробили для цих двох операцій системи позначень і правил, вказали на зв'язок між ними. З того часу це окремий розділ математики. Метод Ньютона-Лейбніца починається заміною кривої, що обмежує площу, яку треба знайти, послідовністю ламаних, що наближається до неї , аналогічно до методу вичерпування. Операція, обернена до диференціювання, називається інтегруванням.

У ХVІІІ ст. розвиткові інтегрального числення найбільше сприяли праці Якоба та Йоганна Бернуллі, Ж.Лагранжа і особливо Л.Ейлера, який довів апарат інтегрального числення майже до сучасного стану.

У ХІV ст. інтегральне числення перебудовують на рівні зрослих вимог математичної строгості О.Коші, Г.Ріман, К.М.Жордан. важливі результати належать українському математикові М.В.Остроградському  і російському вченому П.Л.Чебишеву

У ХХ ст. розвитку інтегрального числення особливо сприяли праці французьких математиків (А.Лебег, Е.Борель, А.Данжуа) і радянських математиків (О.Я.Хінчин, М.М.Лузін, А.М.Колмогоров)/

Учитель Наступна задача буде пов’язана з енергетикою

Учень 6 (розв’язує біля дошки задачу з поясненням, учні конспектують)

Навантаження  на Запорізьку теплоелектростанцію задається функцією             

 f(x) = 3x² + 4x – 2. Визначити витрати електроенергії протягом доби.

Розв’язання:

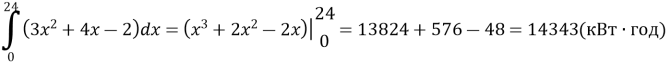
Відповідь: 14343 кВт·год.

Учитель

У хімії теж багато задач розв’язується за допомогою інтегрування. Наприклад, приріст кількості речовини, яка вступила в хімічну реакцію за проміжок часу. Давайте розв’яжемо таку задачу

Учень 7 (розв’язує біля дошки задачу з поясненням, учні конспектують)

Швидкість зміни концентрації речовини, що вступила в реакцію, виражається функцією v = 3t + 1, де t – час (с), v – швидкість (моль/см³). Як зміниться концентрація речовини за час t₁=0 до t₂ =5 c?

Розв’язання

Задача розв’язується методом безпосереднього інтегрування. Оскільки v(t)=C`(t) ,то C(t) – концентрація речовини і первісна для v(t), тому

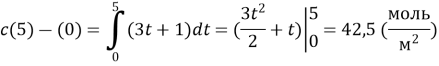
Відповідь. 42,5 моль/м³

Учитель (на фоні презентації) отож ми бачимо, як багато областей людських знань, де відмітився інтеграл. І навіть у літературі. Хто пізнав цю знамениту українську письменницю? (на слайді фото Ліни Костенко, учні відповідають)

Одна з поетичних збірок Ліни Костенко мала назву «Зоряний інтеграл», нажаль вона у свій час була заборонена радянським урядом. В ній була однойменна поема, яка розповідає про наше життя за допомогою математичних термінів, давайте послухаємо уривок

Учень 8

Плюс  мінус  життя.

Таблиця  розмноження.

Квадратний  корінь  із  мрій  романтика.

Два  пишем,  три  помічаєм.

Розношена

щоденна

проста

математика.

Душа  підіймається  до  вищої.

Душа  обчислює  суму  площ:

минуле  -  майбутнє  -  живі  і  знищені  -

правда  -  поезія  -  атомний  дощ.

Дракон  -  Атлант  -  телефон  -  калина  -

віра  -  вірус  -  мільярди  -  нулі...

Життя  оперує  безконечно  малими.

Ми  всі  поодинці  -  також  малі.

Але  з  усмішки,

з  потиску  рук,

з  брехні,  убитої  наповал,

історія  -  найскладніша  з  наук  -

обчислює  ЗОРЯНИЙ  ІНТЕГРАЛ.

Із  найдрібніших  зоряних  крихт!

Вища  математика  світу!

З  СУМИ  БЕЗКОНЕЧНО  МАЛИХ

ВИНИКАЄ  БЕЗКОНЕЧНО  ВЕЛИКЕ.

VІІ.  Підведення підсумків уроку.

На сьогоднішньому уроці ми ще раз переконалися в тому, що математичні теорії є надійним знаряддям в розкритті таємниць природи та законів економічних процесів.

І закінчити урок хочу словами англійського математика Л.Морделла :

- Ніхто не піде далеко в математиці і не стане справжнім математиком, якщо не матиме деяких необхідних рис. У ньому повинні жити Віра, Надія і Допитливість. І найважливіша з цих рис – допитливість. Він повинен раз у раз запитувати себе : чому , як і коли – і це мусить стати головним рушієм, що приводить його в дію.

Ви побачили , що саме допитливість допомогла нам сьогодні досягнути значних результатів.

Тому я бажаю усім, щоб саме ДОПИТЛИВІСТЬ ніколи і ніде не залишала вас.

VІІІ. Домашнє завдання.

Підготовка до контрольної роботи