Урок «Застосування властивостей показникової функції до розв’язування вправ» для 11 класу

11 клас. Конспект уроку № 2

                Тема:     «Застосування      властивостей     показникової     функції     до

розв’язування вправ»

 Мета: формування умінь учнів застосовувати властивості показникової функції до розв’язування вправ. Познайомити учнів з використанням показникової функції під час вивчення явищ навколишнього середовища.

Тип уроку: формування умінь та навичок.

Хід уроку І. Організаційний момент.

ІІ. Перевірка домашнього завдання.

ІІІ. Актуалізація опорних знань. Усно № 1-13.

Додаткові запитання: 

1)                Чи правильно, що показникова функція має екстремуми? ✓ Ні

2)                Чи приймає найбільше значення в деякій точці x₀? ✓ Ні

3)                Чи приймає в деякій точці значення, яке дорівнює 0? ✓ Ні

4)                Чи приймає значення, яке дорівнює 1?

✓  Так

5)                В якій точці x₀?

✓  X₀=1

6)                Чи є показникова функція парною?

✓  Ні

7)                Чи є показникова функція непарною? 

✓  Ні

ІV. Набуття умінь застосовувати властивості показникової функції до розв’язування вправ.  

1)                Усно:

На якому з малюнків, що зображені на дошці, зображений графік функції y = (^𝟏)^x (відповідь: б))  та y = 4^x  (відповідь: в))?

𝟓

                а) 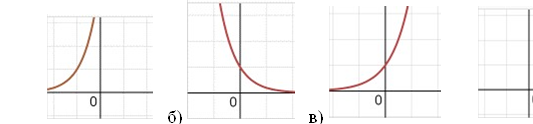    г)         

2)                Побудувати схематично графіки функції:

y = (1/7)ˣ  y = (5,3)ˣ y = (1/√2)ˣ y = (√7)ˣ

3) На дошці намальований графік y=3^x та y=(1/3)^x. Користуючись графіками цих функцій, порівняйте значення виразів:

a)                 3⁵ < 3⁷

b) 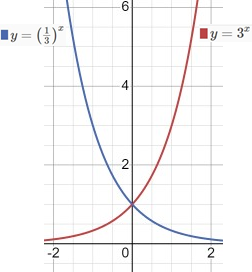               3⁻³ < 3³

c)                 3⁻² > 3⁻¹º

d)                30 > 3-5

e)                 ()⁶ > ()⁸

f)                  ()⁻⁷ > ()⁶

g)                ()⁻⁴ < ()⁻⁶ 

h)                ()⁵  < ()⁰

4)                  Знайти значення функції y=7^x , якщо x = - 2 (1/49) , x=2 (49) , x=0 (1)

5)                  Знайти область значень функції:

  y = -2ˣ                        E(y) = (-∞ ; 0) y = ()^ˣ + 1               E(y) = (1 ; ∞) y = -1/7 ˣ                      E(y) = (-∞ ; 0) y = 4ˣ - 3                       E(y) = (-3 ; 0)

6)                  Порівняйте основу a>0 з одиницею, якщо відомо, що вірна нерівність:

a⁻² > a²                                            0 < a < 1 _{a³ < a}π                                                                       a > 1

a 1                                                     a > 1

a                                                                       0 < a < 1 

7) Що можна сказати про знак х, якщо:

 5ˣ = 10                            x > 0

 0,01ˣ = 2                         x < 0  

10ˣ = 3                              x > 0  

4ˣ = 0,25                          x < 0

V. Сприймання та усвідомлення нового матеріалу

Показникова функція часто використовується для описання різних процесів у природі й техніці. 

Так, радіоактивний розпад позначається формулою: 

𝟏 𝒕 m(t) = mₒ ( )𝑻

𝟐  

Де m(t)  - маса радіоактивної речовини в момент часу t.

m₀ - маса радіоактивної речовини в момент часу  T=0.

T – період напіврозпаду(проміжок часу, за який початкова кількість речовини зменшується удвічі).

За допомогою показникової функції виражається тиск повітря в залежності від висоти підйому, приріст деревини, кількість бактерій, які розмножуються в деякому середовищі тощо. 

Більш детальніше практичне використання показникової функції найчастіше має вигляд:

                y= Ca ^kx

Покажемо, що функції виду y= a ^kx+b можна надати виду y= Ca ^kx Справді a ^kx+b  = a^kx _ a^b. Позначимо a^b=c, тоді a^kx _a^b = Ca ^kx  

А зараз розв’яжемо задачу. 

 При радіоактивному розпаді кількість речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через 1,5 доби?

Розв’язання

За умовою задачі mₒ = 250г, T = 1 доба. За законом радіоактивного розпаду маємо:

𝟏 𝒕 m(t) = mₒ ( )𝑻

𝟐

m(t) = 250 ^t

Знайдемо: 

m(1,5) = 250 ⋅ (0,5)^1,5 ≈ 88,4г

Відповідь: 88, 4 г.

VІ. Підсумок уроку

Записати для будь-яких дійсних значень x і y вірні рівності. 

aˣ ⋅ a^y = a^x+y aˣ : a^y = a^x-y

(ab)ˣ = aˣ ⋅ bˣ

(aˣ)^y = a^xy (𝑎)x = 𝑎ˣ

                  𝑏           𝑏ˣ

VІІ. Домашнє завдання: Підручник Шкіль, сторінка 201-202 № 14-21, 25-26 (усно), 15-17(письмово) та задача: При радіоактивному розпаді кількість речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через 3,5 доби?

Розв’язання:

За умовою задачі mₒ = 250г, T = 1 доба. За законом радіоактивного розпаду маємо:

𝟏 𝒕 m(t) = mₒ ( )𝑻

𝟐

m(t) = 250 ^t

m(3,5) = 250 ⋅ (0,5)^3,5 ≈ 22,1г Відповідь: 22, 1 г .